Funções – 1º parte Conceito Sobrejetora, Injetora e Bijetora Par e

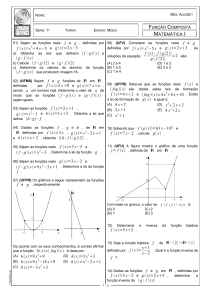
COLÉGIO NOSSA SENHORA DE FÁTIMA
ALUNO(A): ____________________________________________________________ Nº _____
PROF.: Murilo Gomes Santos
DISCIPLINA: Matemática
SÉRIE: 1ª – Ensino Médio
TURMA: ______
DATA: ____________________
LISTA Nº 10 - MATEMÁTICA





Funções – 1º parte
Conceito
Sobrejetora, Injetora e Bijetora
Par e Ímpar
Inversa
Composta
(01) Dados A = {-2, -1, 0, 1, 2}, B = {-1, 0, 1, 3, 4} e a correspondência entre A e B dada por y = x2, com x
faça um diagrama e diga se f é uma função de A em B.
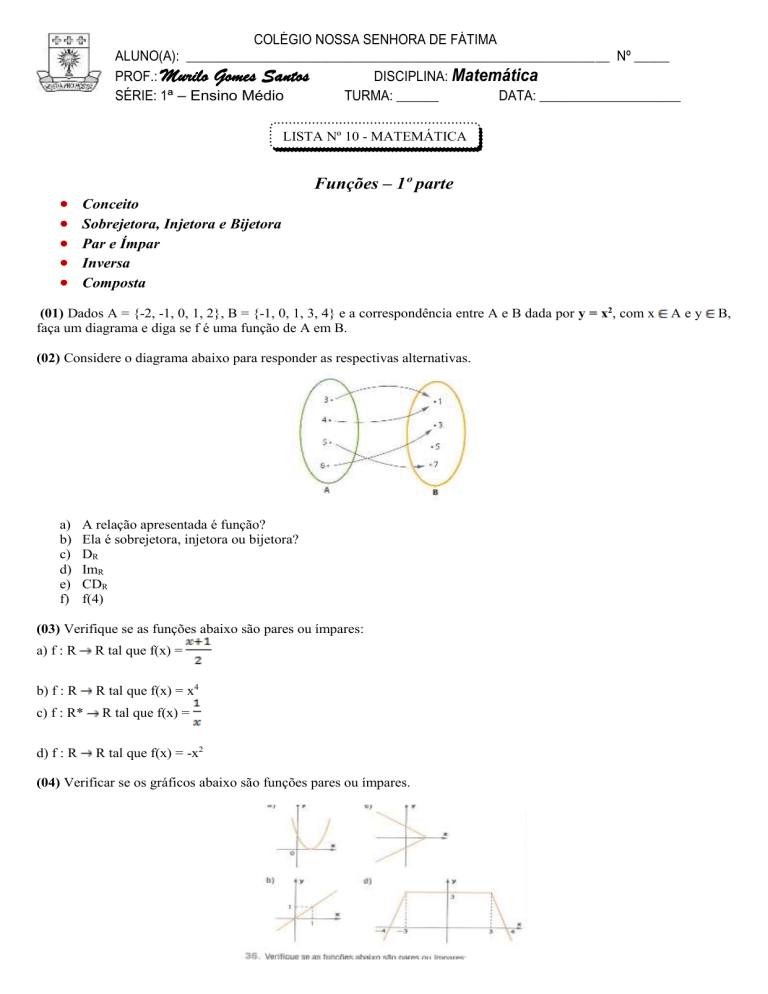
(02) Considere o diagrama abaixo para responder as respectivas alternativas.
a)
b)
c)
d)
e)
f)
A relação apresentada é função?
Ela é sobrejetora, injetora ou bijetora?
DR
ImR
CDR
f(4)
(03) Verifique se as funções abaixo são pares ou ímpares:
a) f : R
R tal que f(x) =
b) f : R
R tal que f(x) = x4
c) f : R*
R tal que f(x) =
d) f : R
R tal que f(x) = -x2
(04) Verificar se os gráficos abaixo são funções pares ou ímpares.
Aey
B,
(05) Determine a função inversa das alternativas abaixo:
a) f(x) = x – 6
b) f(x) = 1 – 2x
c) g(x) =
(06) Dada a função g(x) = 2x – 5, determine o valor de f-1(2) – 3 f(-1).
(07) Considere a função, podemos afirmar que:
(01)D(f(x)) = [ -4, 6[
(02) f(3) + 2 f(0) = 10
(04) f(f(-4)) = 5
(08) Se f(x) > 0 então -4 < x < 3
(16) Se f(x) < 0 então 3< x < 6
(32) Se f(x) = 0 então x = -4 e x = 6
(08) Dadas as funções definidas por f(x) = 3x e g(x) = -2x + 5, assinale a alternativa correta :
a) fog(x) = -6x + 5
b) fog(x) = -6x + 15
c) fog(x) = 6x - 15
d) fog(x) = 6x + 15
e) fog(x) = 6x - 5
(09) As funções reais f e g são definidas por f(x) = 2x + 5 e g(x) = x2 + 1. O valor de g(f(2)) é:
a) 80
b) 15
c) 9
d) 5
e) 8
(10) Sejam f(x) = x2 – 1 e g(x) = x + 2. Determine fog(x) e em seguida fog-1(-3).
(11) Dada a função f(x + 1) = x2, determine:
a) f(4)
b) f(x)
(12) A função real inversível f tal que f(2x – 1) = 6x + 2 tem inversa f-1(x) definida por:
(13) Seja k uma constante real e f e g funções definidas em R tais que f(x) = kx + 1 e g(x) = 13x + k. Determine K
sabendo que fog(x) = gof(x), para todo x real.
(14) Se f(x) = 3x + k e fof(x) = 9x + 20, então k é igual a:
(15) Dada a função f(2x) = 2f(x) e f(8) = 20, então o valor de
é:
(16) Sendo f e g funções de R em R tais que f(x) = x – 3 e f(g(x)) = 2x + 2, então g(f(3)) é igual a:
(17) Dada a função y = 3 –
e f-1 a sua inversa, determine o valor de f-1
(18) Se f(x) é uma função tal que, para todo x real, f(6x) = 4x + 3, então f(3) é igual a:
(19) Para a função f(x) = 2x – 6, existem valores reais a e b, tais que f(a) = f-1(b). Sendo assim a relação entre a e b é dada
por:
(20) Se g(2x + 3) = 4x2 + 6x + 1, então f(1 – x) vale:
Estude com amor e carinho!!!!
Tio Bilo!!!!!!!!!!!!!!!