1) Sendo f(x) = x2 - 1 e g(x) = x + 2, então o conjunto solução da

TRABALHO
Disciplina: Matemática Professor(a): Wilson Jr
Série: 1º Turma: Azul
Nome:
Nº:
Data de entrega: 17/08/12
Bim./Trim: 2º
Evite rasuras. O trabalho deverá ser entregue com capa, perguntas e resoluções.
-
Valor:1,5 pts
Nota:
“A educação para valores certamente supõe uma grande mudança na educação.” Projeto Semeando Valores e Cultivando Vidas.
1) Sendo f(x) = x2 - 1 e g(x) = x + 2, então o conjunto solução da equação f(g(x)) = 0 é:
a) {1, 3}
b) {-1, -3}
c) {1, -3}
d) {-1, 3}
e) { }
2) Sendo f e g funções de R em R, tais que f(x) = 3x - 1 e g(x) = x2, o valor de f(g(f(1))) é:
a) 10
b) 11
c) 12
d) 13
e) 14
3) Se f e g são funções reais tais que f(x) = 2x - 2 e f(g(x)) = x + 2, para todo xR, então g(f(2)) é igual a:
a) 4
b) 1
c) 0
d) 2
e) 3
4) Duas funções, f e g, são tais que f(x) = 3x - 1 e f[g(x)] = 2 - 6x. Nessas condições, o valor de g(-1) é:
a) 3
b) 4
c) 5
d) 6
5) Se f e g são funções de R em R tais que f(x) = 2x - 1 e f(g(x)) = x² - 1, então g(x) é igual a
a) 2x² + 1
b) (x/2) - 1
c) x²/2
d) x + 1
6) Seja f(x) = x² - 3x +2 e g(x) = - 2x + 3 é CORRETO afirmar que:
A) f (g(2)) = 7 B)g (f (2)) = 6
C) f(g(-1)) = 0
D) g (f(0)) = -1
7) Para QUAL VALOR de m, a função f(x) = mx - 4 tem f ( f ( 1 ) ) = - 8?
A) 1
B) 2
C) 3
D) 4
E) 5
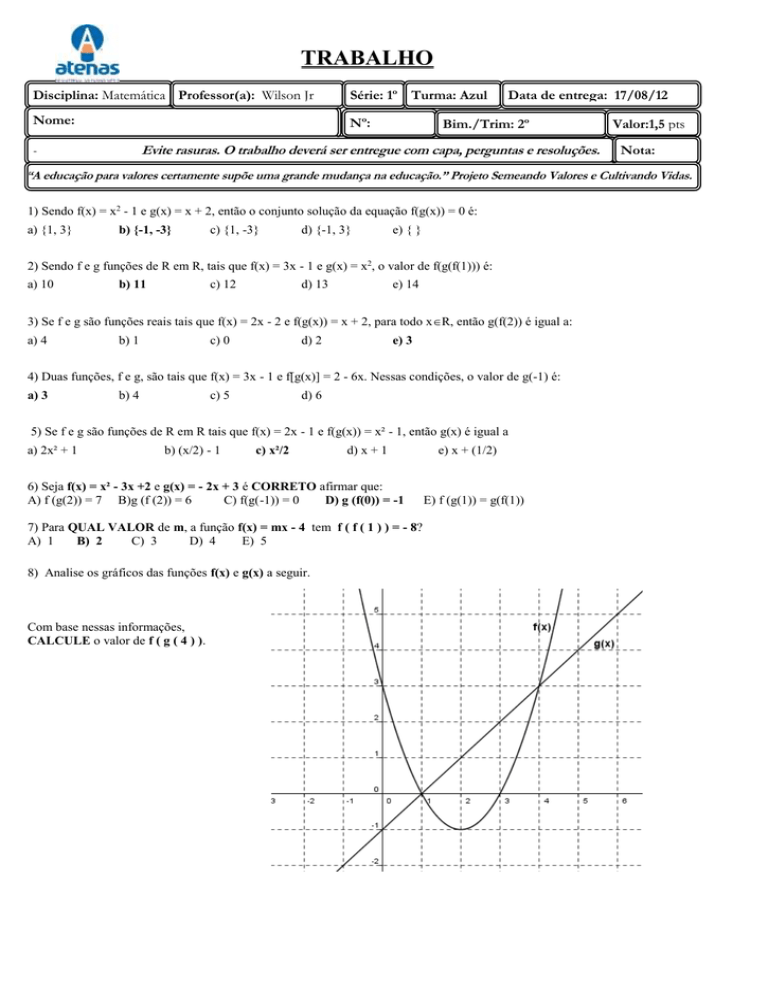
8) Analise os gráficos das funções f(x) e g(x) a seguir.
Com base nessas informações,
CALCULE o valor de f ( g ( 4 ) ).
e) x + (1/2)
E) f (g(1)) = g(f(1))
9) Sendo f uma função par e g, uma função ímpar, e sabendo-se que f    
f
a)
 

 g  2 é igual a:
2
b)

c)
 2
d)

e)

2 e g  2   , pode-se concluir que
 2
10) Sendo f e g duas funções tais que fog(x) = 2x + 1 e g(x) = 2 - x então f(x) é:
a) 2 - 2x
b) 3 - 3x
c) 2x - 5
d) 5 - 2x
11) Obtenha a inversa da função f : IR  IR, definida por f(x) = 2x + 3.
12) Obter a função inversa da f (x) =
2x  4
.
3x  6
13) Se a função real f é definida por f(x)=
a) 1 – x
b) x + 1
c) 1/x -1
f-1(x)= (x-3)/2
f-1(x) = 6 x  4
3x  2
1
1
para todo x > 0, então f (x) é igual a:
x 1
d) 1/x +1
e) 1/(x+1)
14) Seja f a função de IR em IR dada por f(x)= -2x. Um esboço gráfico da função f -1(x), inversa de f, é: ( c )
15) Determine o valor real de a para que f(x) = (x + 1) /(2x + a) possua como inversa a função f -1(x) = (1 – 3x)/(2x - 1).
(a = 3)