Lista de exercícios – 3º EM Seja a função f: D→ IR dada por , de

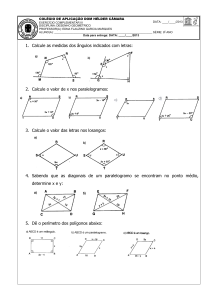
Lista de exercícios – 3º EM
1) Seja a função f: D→ IR dada por f ( x)  2 x  1 , de domínio D = {-2, -1, 0, 2}. Determine o conjunto
Imagem de f.
x2 1
1
2) Seja f: IR*→ IR a função dada por f ( x) 
. Qual é o valor de f (3)  f   ?
x
 3
 x  5, se x é par

3) Dada f: IN → IN tal que 
, calcule:
2
x
,
se
x
é
impar


f 4
a) f (5)
b) f (2)  f (7)
c) f (1) 
d) x tal que f ( x)  14
f (3)
4) As funções f e g são dadas por f ( x)  3x  2m e g ( x)  2 x  1 . Calcule o valor de m, sabendo que
f 0  g 1  3 .
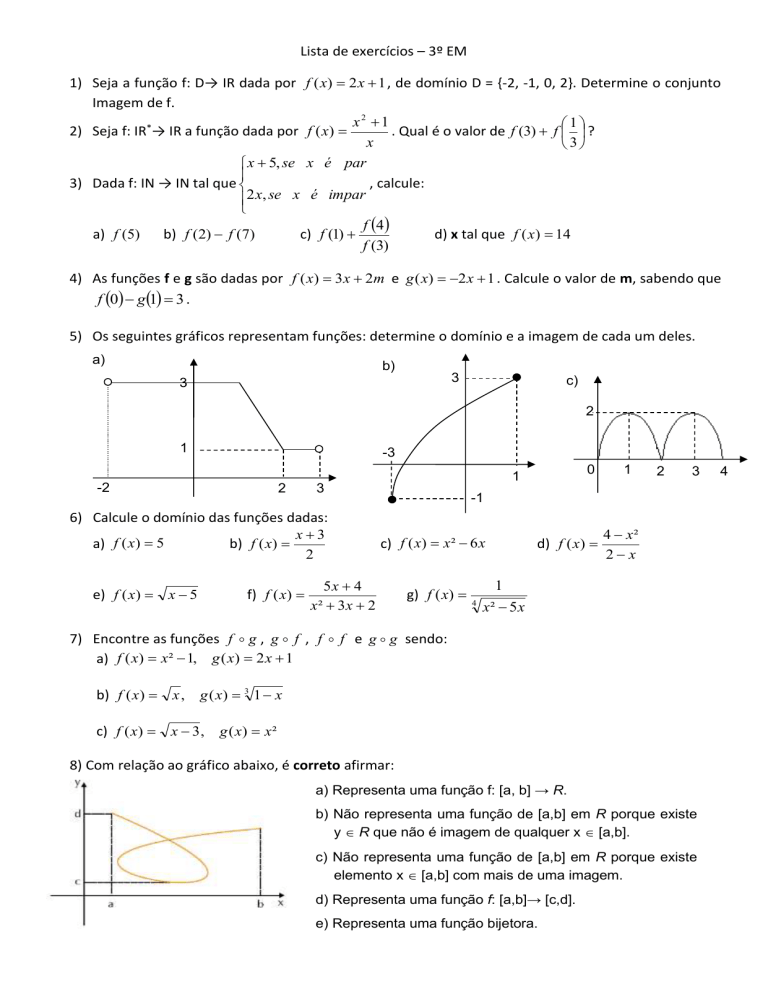
5) Os seguintes gráficos representam funções: determine o domínio e a imagem de cada um deles.
a)
b)
3
3
c)
2
1
-3
-2
2
3
6) Calcule o domínio das funções dadas:
x3
a) f ( x)  5
b) f ( x) 
2
e) f ( x)  x  5
0
1
f) f ( x) 
1
2
3
-1
c) f ( x)  x ²  6 x
5x  4
x ²  3x  2
g) f ( x) 
d) f ( x) 
4  x²
2 x
1
4
x²  5x
7) Encontre as funções f  g , g  f , f  f e g  g sendo:
a) f ( x)  x ²  1, g ( x)  2 x  1
b) f ( x)  x , g ( x)  3 1  x
c) f ( x)  x  3 , g ( x)  x ²
8) Com relação ao gráfico abaixo, é correto afirmar:
a) Representa uma função f: [a, b] → R.
b) Não representa uma função de [a,b] em R porque existe
y  R que não é imagem de qualquer x  [a,b].
c) Não representa uma função de [a,b] em R porque existe
elemento x  [a,b] com mais de uma imagem.
d) Representa uma função f: [a,b]→ [c,d].
e) Representa uma função bijetora.
4
9) Dada as funções f ( x)  5 x e g ( x)  3x  2 , calcule :
b) g ( f (1))
a) f (g (3))
10) Se f ( x)  3x  1 e
c) f ( g (0))  g ( f (1))
fog ( x)  2 x  1 , determine g ( x ) .
11) Sendo f(x) = x2 - 1 e g(x) = x + 2, então o conjunto solução da equação f(g(x)) = 0 é:
a) {1, 3}
b) {-1, -3}
c) {1, -3}
d) {-1, 3}
e) { }
12) Seja f(x) = x² + 2x + 1 e g(x) = – 2x – 1, determine a lei que define f[g(x)] e g[f(x)].
13) Sejam f e g funções reais tais que f[g(x)] = – 10x – 13 e g(x) = 2x + 3. Determine qual é a lei que
define f(x).
14) (METODISTA) Sabendo que f(g(x)) = 3x - 7 e f( x ) = x/3 - 2, então :
a) g(x) = 9x - 15
b) g(x) = 9x + 15
c) g(x) = 15x - 9
d) g(x) = 15x + 9
e) g(x) = 9x – 5
15) (FGV) Considere as funções f(x) = 2x + 1 e g(x) = x2 - 1. Então as raízes da equação f(g(x)) = 0 são:
a) inteiras
b)negativas
c)racionais
d)inversas
16) Seja f(x) = x2+1. Encontre uma função g tal que:
a) f(g(x)) = 9x4+1
b) g(f(x)) = 9x4+1
e)opostas