Funções em Geral

VESTIBULAR: RESUMOS
PROFESSOR: WALTER TADEU
MATEMÁTICA I
FUNÇÕES EM GERAL
Definição. Uma função é uma relação binária entre elementos de um conjunto X e elementos de um conjunto
Y satisfazendo as condições de não ambigüidade e não exceção. A função é chamada de X em Y. Uma
representação na forma de diagramas de conjuntos ilustra esta definição.
Exemplo 1: Considere dois conjuntos, sendo A = {pessoas de uma mesma família} e B = IN.
Observe que, se uma pessoa da família estivesse relacionada a mais de um número do conjunto B, então
ela teria mais de uma idade. O que não é possível. Isto é uma ambigüidade. Ainda nesta situação, caso
alguma pessoa da família não estivesse relacionada a um número de B, ela não teria idade! Isto é uma
exceção.
Exemplo 2: Relação que associa o conjunto de filhos X ao de pais Y.
i) A Relação I não é função, pois há duas ambigüidades: Carlos e Paulo relacionam-se a mais de um
elemento do conjunto Y.
ii) A Relação II não é função, pois houve exceção: Clara não se relacionou com nenhum elemento do
conjunto Y.
iii) As Relações III e IV são funções. Repare que o elemento de Y pode não ser relacionado a nenhum
elemento de X.
Noção de variável: Variável é um elemento genérico de um conjunto. As funções muitas vezes aparecem
como leis ou fórmulas matemáticas onde a partir de um valor (variável) calcula-se outro.
Exemplo. No Brasil, o número de sapato está relacionado com o tamanho do pé, em centímetros, e é dado
pela fórmula N(p) 
5p  28
, onde N é o número do sapato, p é o tamanho do pé, em centímetros.
4
Logo N(p) é uma função de variável p. É uma função, pois não há ambigüidade (ninguém possui dois
tamanhos diferentes no mesmo pé), nem exceção (cada pessoa com pé pode medi-lo).
Uma pessoa com o pé de tamanho de 24 cm, terá seu sapato com número: N (24) 
5.(24)  28
 37
4
1
DOMÍNIO E IMAGEM DE FUNÇÕES
Numa função f: A -> B entre os conjuntos A e B, as variáveis estão no conjunto A e os valores assumidos
(calculados) por elas mediante uma lei ou fórmula estão em B. O conjunto A é chamado Domínio, D(f), da
função e o conjunto B é chamado Contradomínio, CD(f), da função. Os valores encontrados em B
(contradomínio) mediante os cálculos pertencem a um subconjunto de B chamado Imagem, Im(f), da função.
Exemplo. Seja o conjunto A = {0, 1, 2, 3, 4) e B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Vamos definir as funções
f(x): A -> B e g(x): A -> B relacionando os conjuntos. A variável x pertence ao conjunto A, pois é f de A em B.
a) f(x) = 2x. Isto é, cada elemento de B será encontrado multiplicando cada valor de x em A por 2. Temos:
f(0) = 2.(0) = 0
f(1) = 2.(1) = 2
f(2) = 2.(2) = 4
f(3) = 2.(3) = 6
f(4) = 2.(4) = 8
b) g(x) = (x – 3)2. Isto é, cada elemento de B será encontrado calculando o quadrado da diferença entre cada
valor de x em A e 3. Temos:
g(0) = (0 – 3)2 = (-3)2 = 9
g(1) = (1 – 3)2 = (-2)2 = 4
g(2) = (2 – 3)2 = (-1)2 = 1
g(3) = (3 – 3)2 = (0)2 = 0
g(4) = (4 – 3)2 = (-1)2 = 1
Quando o domínio de uma função é o conjunto dos números reais (IR) significa que qualquer número real
pode ser colocado como variável na fórmula ou lei que define a função f(x). No entanto, nem sempre isso é
possível. Veja os exemplos.
a) O domínio da função definida por f: IR -> IR, f(x) = 3x + 4 é D(f) = IR, pois qualquer valor de x, poderá ser
calculado. A imagem também será Im(f) = IR.
b) O domínio da função dada por f ( x ) 
x3
é D(f) = IR – {1}. Isto é, o único real que não pode ser
x 1
colocado no lugar de x é 1, pois x – 1 = 1 – 1 = 0 está no denominador e ele não pode ser nulo.
c) O domínio da função dada por f ( x ) 
x  2 é D(f )  x  IR / x  2} , pois o radicando negativo na raiz
quadrada não está definido no conjunto dos reais.
2
ANÁLISE DE GRÁFICO DE FUNÇÕES
O gráfico de uma função, quando corretamente interpretado, pode nos fornecer inúmeras informações sobre
o comportamento da função. Observaremos características gerais de funções e vamos interpretá-las
graficamente.
Exemplo. Observe no gráfico ao lado os intervalos onde a função cresce, decresce e seus pontos de máximo
e mínimo.
Os valores de “x” e de y = f(x) são ilimitados. Isto é:
D f   ;  IR
Im f   ;  IR
Pela lei da função, temos:
- f (3) = (3) 3 
- f ( 0 ) = ( 0) 3 
-
3
27
81
(3) 2  27 
   40,5
2
2
2
3
(0) 2  0
2
f 1 = 13  12  1 
3
2
3
1
   0,5
2
2
3
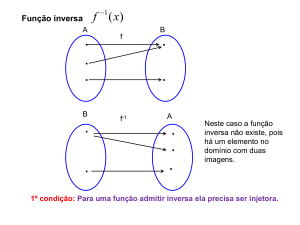
FUNÇÃO INVERSA: Dada uma função f: A → B, se f é bijetora, então se define a função inversa como sendo
a função de B em A, tal que f -1(y) = x .
Veja a representação mostrada no quadro.
Observações:
a) para obter a função inversa, basta permutar as variáveis
x e y.
b) o domínio de f -1 é igual ao conjunto imagem de f.
c) o conjunto imagem de f -1 é igual ao domínio de f.
d) os gráficos de f e de f -1 são curvas simétricas em
relação à reta y = x, ou seja, à bissetriz do primeiro
quadrante.
Exemplo: Determine a inversa da função definida por y = 2x + 3.
i) Permutando as variáveis x e y, fica: x = 2y + 3.
ii) Explicitando y em função de x, vem: 2 y  x  3  y 
x3
, que define a função inversa da função
2
dada.
Observação: O gráfico mostrado a seguir representa uma função e a sua inversa.
Observe que as curvas representativas de f e de f-1 são simétricas em relação à reta y = x, que é bissetriz do
primeiro e terceiro quadrantes.
FUNÇÃO COMPOSTA: Chama-se função composta (ou função de função) à função obtida substituindo-se a
variável independente x, por uma função.
Simbologia: fog(x) = f(g(x)) ou gof (x) = g(f(x)).
Veja o esquema a seguir:
Observação: A composição de funções não é comutativa. Isto é, em geral temos que fog ≠ gof.
Exemplo: Dadas as funções f(x) = 2x + 3 e g(x) = 5x, pede-se determinar gof(x) e fog(x). Temos:
i) gof(x) = g[f(x)] = g(2x + 3) = 5(2x + 3) = 10x + 15
ii) fog(x) = f[g(x)] = f(5x) = 2(5x) + 3 = 10x + 3
4