Funções trigonométricas inversas

Funções trigonométricas inversas
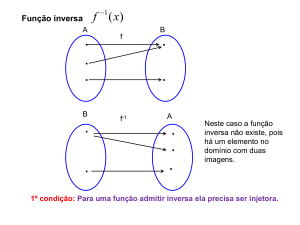
Uma função f, de domínio D possui inversa somente se f for
bijetora, por este motivo nem todas as funções trigonométricas
possuem inversas em seus domínios de definição, mas
podemos tomar subconjuntos desses domínios para gerar
novas função que possuam inversas.
Exemplo: A função f(x)=cos(x) não é bijetora em seu domínio
de definição que é o conjunto dos números reais, pois para um
valor de y correspondem infinitos valores de x. Por exemplo, se
cos(x)=1, podemos tomar x=0, x=2 , x=4 , x=-2 , etc, isto é
x=2k , onde k é um número inteiro, isto quer dizer que não
podemos definir a inversa de f(x)=cos(x) em seu domínio.
Devemos então restringir o domínio para um subconjunto dos
números reais onde a função é bijetora.
Como as funções trigonométricas são periódicas, existem
muitos intervalos onde elas são bijetoras. É usual escolher
como domínio, intervalos onde o zero é o ponto médio ou o
extremo esquerdo e no qual a função percorra todo seu
conjunto imagem.
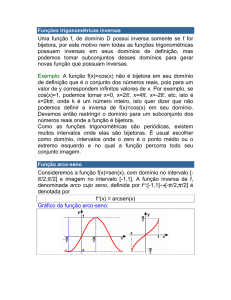
Função arco-seno
Consideremos a função f(x)=sen(x), com domínio no intervalo [/2, /2] e imagem no intervalo [-1,1]. A função inversa de f,
denominada arco cujo seno, definida por f-1:[-1,1] [- /2, /2] é
denotada por
f-1(x) = arcsen(x)
Gráfico da função arco-seno:
Função arco-cosseno
Seja a função g(x)=cos(x), com domínio [0, ] e imagem [-1,1].
A função inversa de f, denominada arco cujo cosseno é
definida por g-1:[-1,1] [0, ] e denotada por
g-1(x) = arccos(x)
Gráfico da função arco-cosseno:
Função arco-tangente
Dada a função f(x)=tan(x), com domínio (- /2, /2) e imagem
em R, a função inversa de f, denominada arco-tangente é
definida por f-1:R (- /2, /2) e denotada por
f-1(x) = arctan(x)
Gráfico da função arco-tangente:
Função arco-cotangente
Dada a função f(x)=cot(x), com domínio (0, ) e imagem em R,
a função inversa de f, denominada arco-cotangente é definida
por f-1:R (0, ) e denotada por
f-1(x) = arccot(x)
Gráfico da função arco-cotangente: