Slide 1 - Colégio Energia Barreiros

1
f ( x)
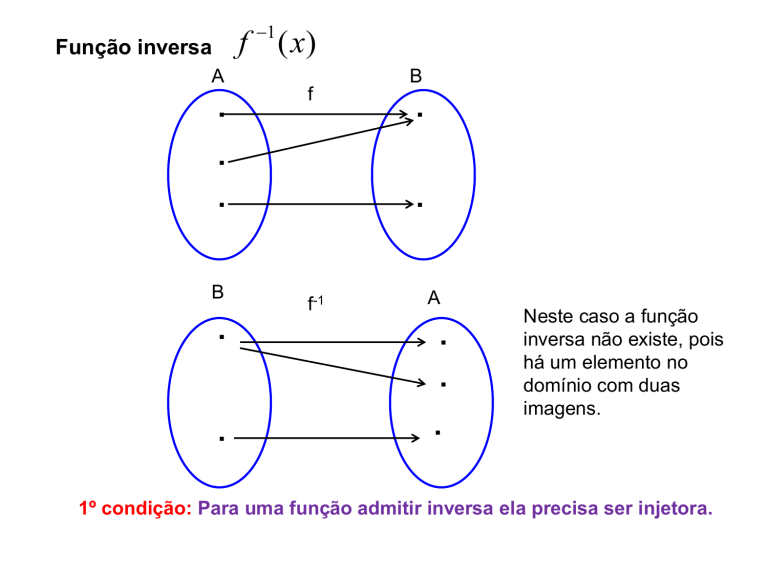
Função inversa
A
.
B
f
.
.
B
.
.
f-1
A
.
.
.
.
.
Neste caso a função
inversa não existe, pois
há um elemento no
domínio com duas
imagens.
1º condição: Para uma função admitir inversa ela precisa ser injetora.
A
f
B
.
.
.
.
.
.
.
.
.
.
f-1
.
.
Neste caso a função
inversa não existe, pois
há elementos no
domínio sem imagens.
2º condição: Para uma função admitir inversa ela precisa ser sobrejetora.
Condição de existência da função inversa:
Dada a função f:AB a sua inversa f -1 BA só existe se f for bijetora.
Se a função f é a inversa de g, então g é a inversa de f.
Se f e g são inversas, então fog(x) = gof(x) = x (função identidade)
Identificação gráfica de funções inversas:
 Bissetriz dos
quadrantes
ímpares.
Duas funções são inversas quando seus gráficos são
simétricos em relação a bissetriz dos quadrantes ímpares.
Como achar a lei de formação da inversa.
Trocar f(x) por y.
Isolar x.
Trocar x por f-1(x)
Ex:
f ( x)  2 x  3
y  2x  3
y  3  2x
y3
y3
1

x
f ( y) 
2
2