127040446378626_Capitulo

Capítulo 2 - Funções
• Prof. Daniel Keglis
• Matemática
2.1) Noção de Função
Observe a relação abaixo:
Lado do quadrado x perímetro
* Observe que o perímetro do quadrado é dado
em função da medida do seu lado, isto é, o
perímetro depende da medida do lado.
p = 4l , onde :
p é uma variável dependente de l e l é uma
variável independente.
2.1.1) Relação entre conjuntos
Sejam os conjuntos A e B, onde x pertence a A
e y pertence a B.
y = 3x
• Note que: todos os elementos de A tem um
correspondente em B
Veja outras relações e observe
representam um função f de A em B.
Não é função
É função
y = x4
quais
Não é função
2.1.2) Definição de função
Dados dois conjuntos não vazios A e B, uma função de
A em B é uma regra que diz como associar cada
elemento de x ϵ A a um único elemento y ϵ B
2.1.3) Domínio, Contradomínio e
Imagem da função
Dada uma função f de A em B
y = f(x)
Para obtermos Domínio D(f), Contradomínio
CD(f) e Imagem Im(f) de uma função, faremos
a seguinte análise.
Sejam os conjuntos A e B, onde x ϵ A e y ϵ B e f(x) = 2x
D(f) = {0,1,2,3}
CD(f) = {0,1,2,3,4,5,6}
Im(f) = {0,2,4,6}
2.1.4) Valor Numérico
Veja o exemplo:
Seja a função f(x) = x2 + 2 , o valor numérico
para:
f(-1) = (-1)2 + 2 = 3
f(0) = (0)2 + 2 = 2
f(3) = (3)2 + 2 = 11
2.2) Gráficos
Os gráficos e tabelas encontrados em
revistas, jornais e livros, querem retratar uma
determinada situação. Esses gráficos e tabelas
representam funções e por meio deles
podemos obter informações sobre a situação
em estudo.
Exemplo
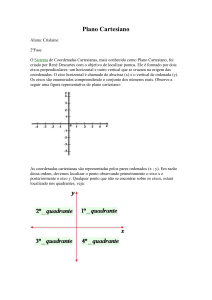
2.2.1) Coordenadas Cartesianas
Usamos a notação (x,y) para indicar o par
ordenado de números reais que serão
representados no sistema de eixos ortogonais.
Os eixos ortogonais dividem o plano
cartesiano em quatro regiões chamadas de
quadrantes, conforme representação abaixo:
Dado um ponto P desse plano, dizemos que
os números a e b são coordenadas cartesianas
do ponto P. A coordenada a chamamos de
abscissa e a coordenada b é a ordenada.
Vamos localizar no plano cartesiano os
pontos: A(4,1); B(1,4); C(-2,-3); D(2,-2); E(-1,0);
F(0,3) e O(0,0).
2.2.2) Construção de gráficos
Para construir o gráfico de uma função dada
no plano cartesiano devemos:
• Construir uma tabela com valores.
• A cada par ordenado associar um ponto do
plano cartesiano.
• Esboçar o gráfico.
Exemplo
2.2.3) Análise de gráficos
Reconhecendo se o gráfico representa uma
função.
É função
Não é função
• Determinando domínio e imagem da função
através do gráfico.
• Determinando onde a função cresce e onde
ela decresce.
Crescente: ]-6,-3] U [2,6[
Decrescente: [-3,2]
Crescente: ]-∞,3]
Constante: [3,+∞[
2.3) Função definida por várias
sentenças
x  2, se x  4

f ( x )  3, se x  4
6 - x, se x  4

Estudo do domínio de uma função
Veremos no caderno os exemplos para este
estudo.
2.4) Função Inversa
Definição: Dada uma função f: A
B, bijetora,
denomina-se função inversa de f a função
g: B A tal que f(x) = y e
g(y) = x, com x que
pertence a A e y que pertence a B.
Observe:
D(f) = Im(g)
D(g) = Im(f)
Processo para determinar a função
inversa
•
•
•
•
Escrevemos f(x) = y.
Trocamos y por x e x por y.
Determinamos y em função de x.
Escrevemos y = f -1(x).
2.5) Função Composta
Definição: Dada uma função f: A
B, e ,
g: B
C denomina-se função composta de
em f a função gof: A
C, que é definida por
(gof)(x) = g(f(x)), x pertencente a A.
Exemplo: