Revisão de Função

Revisão de Função
5. (Uepb 2014) Uma função inversível f, definida em
x5
R  3 por f  x  
, tem contradomínio R  y0 ,
x3
onde R é o conjunto dos números reais. O valor de y0 é:
Inversa e Composta
Professor Gaspar
a) 1
d) 1
1. (Espcex (Aman) 2015) Considere a função bijetora
b) 3
e) zero
c) 2
6. (Espcex (Aman) 2013) Na figura abaixo está
representado o gráfico de uma função real do 1º grau f(x).
f : 1,       ,3, definida por f(x)  x2  2x  2 e
seja (a,b) o ponto de intersecção de f com sua inversa. O
valor numérico da expressão a  b é
a) 2.
b) 4.
c) 6.
d) 8.
e) 10.
2. (Unicamp 2015) Seja a um número real positivo e
considere as funções afins f(x)  ax  3a e g(x)  9  2x,
definidas para todo número real x.
a) Encontre o número de soluções inteiras da inequação
f(x)g(x)  0.
b) Encontre o valor de a tal que f(g(x))  g(f(x)) para
todo número real x.
A expressão algébrica que define a função inversa de f(x) é
x
1
a) y   1
b) y  x 
2
2
c) y  2x  2
d) y  2x  2
e) y  2x  2
3. (Uepg 2014) Considerando as funções f(x) e g(x), tais
que f(x) 
x3
5x
, assinale o que for
e f(g(x)) 
4
4x  4
correto.
01) O domínio de g(x) é {x 
3
02) g1(0)  .
2
1
04) g(1)   .
2
1
08) g(f(5))  .
3
16) O domínio de f(x) é {x 
| x  1}.
| x  3}.
7. (Espcex (Aman) 2013) Sejam as funções reais
f  x   x2  4x e g  x   x  1. O domínio da função
f(g(x)) é
a) D  x  | x  3 ou x  1
b) D  x 
| 3  x  1
c) D  x 
| x  1
d) D  x 
| 0  x  4
e) D  x 
| x  0 ou x  4
8. (Uern 2013) Sejam as funções f(x)  x  3 e
g(x)  x 2  2x  4. Para qual valor de x tem
f(g(x))  g(f(x))?
a) 2
b) 3
c) 4
d) 5
4. (Unicamp 2014) Considere as funções f e g, cujos
gráficos estão representados na figura abaixo.
9. (Esc. Naval 2013) Considere f e g funções reais de
1
e g(x)  2x 2.
4x  1
Qual é o domínio da função composta (fog)(x)?
variável real definidas por, f(x) 
a) R
O valor de f(g(1))  g(f(1)) é igual a
a) 0.
b) – 1.
c) 2.

c)  x 

d) 1.

e)  x 


b)  x 

1 

2 2
2 2
1
1 
1

|x 
d)  x  | x  , x 

4
4
2 2

1
1 
|x ,x

4
2 2
|x
1
,x
10. (Uepb 2013) Dada f(x)  x2  2x  5, o valor de
f(f(1)) é:
a) – 56
b) 85
c) – 29
d) 29
e) – 85
15. (Ufsj 2012) Sendo a função f  x   ax  b, tal que
11. (Uern 2013) Se o gráfico da função inversa de uma
função f(x) do 1º grau tem como raiz x = 6 e o coeficiente
angular de f(x) é igual a 2, então o gráfico que melhor
representa f(x) é
c) f  x   3x  4
f  f  x    9x  8, é CORRETO afirmar que
x
a) f 1  x    2
3
 x  2
d) f 1  x  
3
16. (Pucrj 2012) Sejam f(x)  2x  1 e g(x)  3x  1.
Então f(g(3))  g(f(3)) é igual a:
a) – 1
b) 0
c) 1
d) 2
e) 3
x 3
.O
2x  1
domínio de g(x) e a função inversa de g(x) são,
respectivamente,
x3
a) x  ;x  1 2 e g1  x  
2x  1
x  3
b) x  ;x  1 2 e x  3 e g1  x  
2x  1
x  3
c) x  ;x  1 2 e g1  x  
2x  1
x3
d) x  ;x  1 2 e x  3 e g1  x  
2x  1
17. (Ufsj 2012) Considere a função g  x  
a)
b)
18. (Ufba 2012) Determine f 1(x) , função inversa de
c)
x
 1
   , sabendo que f(2x  1) 
3
3x
6
 
para todo x   2 .
f:
d)
12. (Uern 2012) Sejam as funções compostas
f(g(x))  2x  1 e g(f(x))  2x  2. Sendo g(x)  x  1,
então f(5)  g(2) é
a) 10.
c) 7.
b) f  0   8
b) 8.
d) 6.
13. (Espm 2012) Sejam f e g funções reais tais que
f  2x  1  2x  4 e g  x  1  2x  1 para todo x  R.
Podemos afirmar que a função fog(x) é igual a:
a) 2x – 1
b) x + 2
c) 3x + 1
d) 2x
e) x – 3
14. (Pucrj 2012) Sejam f(x)  x2  1 e g(x)  x 2  1.
Então a equação f(g(x))  g(f(x))  2 tem duas soluções
reais. O produto das duas soluções é igual a:
a) −2
b) −1
c) 0
d) 1
e) 2
 3 
19. (Uepb 2012) Dada a função bijetora
3x  2
f(x) 
, D(f )   1, o domínio de f 1(x) é
x 1
a)  3
b)
c)
 1
e)
 2
  
 3
d)
 1
20. (Uern 2012) Seja f(x) uma função do primeiro grau que
intercepta os eixos cartesianos nos pontos (0, 4) e (2, 0). O
produto dos coeficientes da função inversa de f(x) é
a) 2.
b) – 1.
c) 4.
d) – 2.
21. (Uepg 2011) Sobre uma função afim f(x) = ax + b,
assinale o que for correto.
01) Se a > 0 e b < 0 então f(x) é crescente e possui raiz
negativa.
02) Se o gráfico de f(x) passa pelos pontos,
(–1, 1) e (3, 5) então f(f(–3)) = 1.
1
3
x .
2
4
08) Se b = – 3 e f(f(–2)) = – 5 então a = 3.
16) Se a.b > 0 a raiz de f(x) é um número positivo.
04) Se f(x) + f(x – 3) = x então f(x) =
22. (Epcar (Afa) 2011) Considere o conjunto
A  0,1,2,3 e a função f : A  A tal que f  3   1 e
f  x   x  1, se x  3 . A soma dos valores de x para os
quais  fofof  x   3 é
a) 2
c) 4
b) 3
d) 5
f(g(x))  g(f(x))  2ax  12a  2ax  6a  9
a
Resposta da questão 3: 01 + 02 + 04 + 08 = 15.
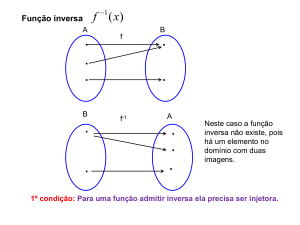
Lembrando que uma função está bem definida apenas
quando são fornecidos o domínio, o contradomínio e a lei
de associação, vamos supor que f : A   e
g:B   .
Desde que f(x) 
2
23. (Fuvest 2011) Sejam f(x) = 2x - 9 e g(x) = x + 5x + 3. A
soma dos valores absolutos das raízes da equação
f  g  x    g  x  é igual a
a) 4
d) 7
b) 5
e) 8
f(g(x)) 
c) 6
Gabarito:
Resposta da questão 1: [B]
Os pontos comuns de uma função com a sua inversa são da
forma (a, a), portanto, para determinar estes pontos
devemos considerar f(x)  x na função dada. Daí, temos:
x  x2  2x  2  x2  x  2  0  x  1 [1,  ) ou x  2.
Logo, o ponto (a, b) pedido é (2, 2) e 2  2  4.
Resposta da questão 2:
a) Sendo a  0, temos
9

f(x)g(x)  0  a(x  3)  x    0

2
9
 3  x  .
2
Portanto, segue que x  {2,  1, 0, 1, 2, 3, 4}, ou seja, a
1
.
2
x3
5x
, temos
e f(g(x)) 
4
4x  4
g(x)  3
5x
g(x)  3


4
4x  4
4
2x  3
 g(x) 
.
x 1
[01] Correto. Supondo que se queira determinar o maior
subconjunto B dos números reais para o qual g está
definida, é fácil ver que B  {x  | x  1}.
[02] Correto. Calculando a inversa de g, obtemos
y
2x  3
 yx  y  2x  3
x 1
 yx  2x   y  3
y3
x
,
2y
x3
. Desse modo, encontramos
2x
3
facilmente g1(0)  .
2
ou seja, g1(x) 
[04] Correto. Com efeito, pois g(1) 
2  1 3
1
 .
1 1
2
[08] Correto. De fato, temos g(f(5))  g(2) 
inequação possui 7 soluções inteiras.
22 3 1
 .
2 1
3
f(g(x))  ag(x)  3a  a(9  2x)  3a  2ax  12a
[16] Incorreto. Supondo que se queira determinar o maior
subconjunto A dos números reais para o qual f está
definida, é fácil ver que A  .
e
Resposta da questão 4: [D]
g(f(x))  9  2f(x)  9  2(ax  3a)  2ax  6a  9.
Do gráfico, sabemos que g(1)  0 e f(1)  1. Logo, como
b) Tem-se que
f(0)  1 e g( 1)  0, obtemos
Logo, vem
f(g(1))  g(f(1))  f(0)  g( 1)
 1 0
 1.
x 2  2x  4  3  (x  3)2  2(x  3)  4  x 2  2x  3  x 2  6x  9  2x  6
 6x  15  3
Resposta da questão 5: [D]
 x  3.
Resposta da questão 6: [C]
Seja f :  a função definida por f(x)  ax  b.
O valor inicial de f é a ordenada do ponto de interseção do
gráfico de f com o eixo y, ou seja, b  1. Logo, como o
Resposta da questão 9: [B]
fog(x) 
gráfico de f passa pelo ponto ( 2, 0), temos que
0  a  ( 2)  1  a 
Portanto, f(x) 
x
1
2
4  2x  1

1
2
8x  1
Logo,
1
.
2
8x 2  1  0  x 2 
x
 1 e sua inversa é tal que
2
y
 1  y  2  (x  1)  f 1(x)  2x  2.
2
Resposta da questão 7: [A]
1
1
1
x
ex
8
2 2
2 2
Portanto, o domínio será dado por:
1
1 

D  x  | x 
ex
.
2 2
2 2

Resposta da questão 10: [D]
Como f(1)  (1)2  2  (1)  5  4, segue que
Temos que
f(f(1))  f(4)  42  2  4  5  29.
f(g(x))  (x  1)2  4(x  1)
 x 2  2x  1  4x  4
 x 2  2x  3
 (x  3)(x  1).
Assim, a função f g está definida para os valores de x
tais que
(x  3)(x  1)  0  x  3 ou x  1,
Resposta da questão 11: [A]
Lembrando que uma função só está bem definida quando
conhecemos o seu domínio, contradomínio e a lei de
associação, vamos supor que f :  com
f(x)  ax  b. Logo, como a taxa de variação de f é igual a
2, segue-se que f(x)  2x  b.
A lei da função inversa de f é dada por
y  2x  b  x  2y  b
ou seja,
 f 1(x) 
D  {x 
| x  3 ou x  1}.
Resposta da questão 8: [B]
Lembrando que uma função só está bem definida quando
conhecemos o seu domínio, contradomínio e a lei de
associação, vamos supor que f :  e g :  .
1
b
x .
2
2
Desse modo, sendo o zero de f 1 é igual a 6, vem
0
1
b
 6   b  6.
2
2
Além disso, por exemplo, a função g f está definida
Portanto, o gráfico que melhor representa a função afim f
é o da alternativa [A].
apenas quando o contradomínio de f é igual ao domínio
de g.
Resposta da questão 12: [A]
Desse modo, o valor de x para o qual se tem
f(g(x))  g(f(x)) é
Sabendo que g(f(x))  2x  2 e g(x)  x  1, vem
g(f(x))  f(x)  1  2x  2  f(x)  1  f(x)  2x  3.
Portanto,
f(5)  g(2)  2  5  3  2  1  10.
OBS: Poderíamos também ter considerado a  3.
Resposta da questão 13: [D]
Resposta da questão 16: [A]
Fazendo t  2x  1, vem
Como f(3)  2  3  1  7 e g(3)  3  3  1  10, segue que
x 1
.
2
x  2t  1  t 1(x) 
f(g(3))  g(f(3))  f(10)  g(7)
 2  10  1  (3  7  1)
 20  1  21  1
Logo,
x 1
 x 1 
f 2
 1  2 
 4  f(x)  x  3.


2
2
Por outro lado, se u  x  1, então
x  u  1  u1(x)  x  1.
 1.
Resposta da questão 17: [C]
O domínio da função g é o conjunto de valores de x para os
quais
1
2x  1  0  x   ,
2
Desse modo,
g(x  1  1)  2  (x  1)  1  g(x)  2x  3.
Portanto,
f g(x)  f(g(x))

1
ou seja, D   x  ; x   .
2


A função inversa de g é tal que
 g(x)  3
 2x  3  3
y
 2x.
Resposta da questão 14: [B]
f(g(x))  g(f(x))  2
 x  1
2
2


 1  x2  1
2
 1  2
x 4  2x 2  2  x 4  2x 2  2
x2  1  0
Calculando o produto P das raízes temos: P  1: 1  1.
Resposta da questão 15: [D]
f  f  x    9x  8
a  ax  b   b  9x  8
x3
y3
x
2x  1
2y  1
 2yx  y   x  3
x  3
 g1(x) 
.
2x  1
Resposta da questão 18:
Fazendo t  2x  1, segue que x  2t  1  t 1 
Substituindo x por t 1 na lei da função f, vem:
x 1
x 1
 x 1 
2
f 2
 1 
 f(x) 
.
x 1


2
3x  9
3
6
2
Portanto,
y 1
x
 3xy  9x  y  1
3y  9
 y(3x  1)  9x  1
9x  1 1
 y 1 
 f (x).
3x  1
a2 x  b  a  1  9x  8
a2  9, logo a  3 ou a  3.
Considerando a  3, temos:
Resposta da questão 19: [A]
b  3  1  8
Se f(x) 
b2
 x  2
Logo f  x   3x  2 e f 1  x  
3
3x  2
, com D(f) 
x 1
 {1}, então
x 1
.
2
y
3x  2
 y(x  1)  3x  2
x 1
 x(y  3)  y  2
y2
x
.
y3
Portanto, y  3  0  y  3 e, assim, D(f 1) 
 f(x)  ax  b
 f(x)  f(x  3)  1x
 (ax  b)  (a(x  3)  b)  1x
 ax  b  ax  3a  b  1x
 {3}.
Resposta da questão 20: [B]
Seja f(x)  ax  b a lei da função afim cujo gráfico
intersecta os eixos cartesianos nos pontos (0, 4) e (2, 0).
Como o gráfico de f intersecta o eixo das ordenadas no
ponto (0, 4), segue que b  4. Por outro lado, se (2, 0) é
o ponto de interseção com o eixo das abscissas, então
0  a  2  4  a  2.
Daí, f(x)  2x  4 e, assim, a lei da função f 1 é tal que
1
x  2y  4  2y  x  4  f 1(x)   x  2.
2
1
Portanto, o produto pedido é igual a   2  1.
2
 2ax  2b  3a  1x
Logo :
1

a
2a  1
2

2b  3a  0  b  3

4
Portanto:
1
3
 f(x)  x 
2
4
Item (08) – Falso
 Para b  3  f(x)  ax  3
 f( 2)  2a  3
 f(f( 2))  a  2a  3)   3
 f(f( 2))  2a2  3a  3
Portanto:
f(f( 2))  5
Logo
 2a2  3a  3  5
 2a2  3a  2  0
Temos :
Resposta da questão 21: 02 + 04 = 06.
Item (01) – Falso
Sendo f(x) = ax + b, temos para a > 0 e b < 0 o gráfico a
seguir:
a1  2 ou a2 
1
2
Item (16) – Falso
Se a  0 e b  0  ab  0
.
Logo :
A raiz de f(x)  ax  b será negativa.
Resposta da questão 22: [B]
Portanto, f(x) = ax + b é crescente, porém não possui raiz
negativa (intercepta x num valor positivo)
Item (02) – Verdadeiro
Considerando f(x) = ax + b, temos:
( 1,1)  f( 1)  a( 1)  b  a  b  1
a  1

,

( 3,5)  f( 3)  a( 3)  b  3a  b  5
b  2
então f(x)  x  2
Portanto:
f(3)  (3)  2  1
Logo:
f(f(3))  (1)  2  1
Item (04) – Verdadeiro
f[f(f(x))] =3
f(f(x)) = 2
f(x) =1
Portanto, x = 3.
Resposta da questão 23: [D]
2
f(g(x)) = 2.(x + 5x + 3) – 9
2
f(g(x)) = 2x + 10x + 6 – 9
2
f(g(x)) = 2x + 10x – 3
Fazendo f(g(x)) = g(x) temos:
2
2
2x + 10x -3 = x + 5x + 3
2
x + 5x -6 = 0
Resolvendo temos x = - 6 ou x = 1
Logo: 6  1  7