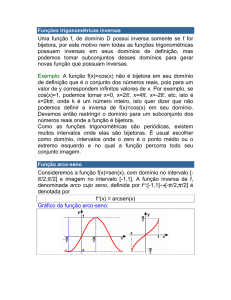
LISTA 2
Assunto: Função Inversa
Prof.: Valdex Santos
Monitoras: Hilary e Michele
1- Determinar a lei que define a função inversa da função bijetora 𝑓: ℝ → ℝ tal que
𝑓 (𝑥) = −5𝑥 + 1.
2- Considerar a função de domínio real dada pela lei 𝑓 (𝑥) = 𝑥³
a) Qual é a lei da função inversa de 𝑓?
b) Sem construir os gráficos, determine os pontos de intersecção dos gráficos de 𝑓 e
𝑓 −1 .
3- Determine a lei que define a função inversa de cada função 𝑓: ℝ → ℝ abaixo:
a) 𝑓 (𝑥) = 4𝑥 + 9
b) 𝑔 (𝑥) = −2𝑥 + 3
1
c) h(x) = −7x − 2
d) m(x) =
𝑥+5
3
e) 𝑛(𝑥) = 𝑥³ + 1
5
f) p(x) = √2𝑥
4- Escreva a lei da função inversa de cada função 𝑓: ℝ → ℝ abaixo:
a) 𝑓(𝑥) = −𝑥 + 3
b) 𝑔(𝑥) = 2𝑥
𝑥
c) 𝑝 (𝑥) = 3 − 2
d) 𝑘(x) = 2x + 1
5- Dada a função real 𝑓: ℝ → ℝ, cuja lei é 𝑓(𝑥) = (𝑥 – 1) 2 – (𝑥 + 2) 2 + 3. Seja a
sua função inversa denotada por 𝑓 −1 . O conjunto solução da equação 𝑓(𝑥) =
𝑓 −1 (𝑥) é:
(A) {8}.
(B) {– 8}.
(C) {0}.
(D) ℝ
(E) ∅
6- (Ufrrj) Seja 𝑓: ℝ → ℝ uma função definida por 𝑓(𝑥) = 𝑎𝑥 + 𝑏. Se o gráfico da
função 𝑓 passa pelos pontos 𝐴 (1, 2) e 𝐵 (2, 3), a função 𝑓 −1 (inversa de 𝑓 ) é :
𝑎) 𝑓 −1 (𝑥) = 𝑥 + 1
𝑏) 𝑓 −1 (𝑥) = − 𝑥 + 1
𝑐) 𝑓 −1 (𝑥) = 𝑥 − 1
𝑑) 𝑓 −1 (𝑥) = 𝑥 + 2.
𝑒) 𝑓 −1 1 (𝑥) = − 𝑥 + 2.
7- (Ufsm) Seja 𝑓: ℝ → ℝ uma função definida por 𝑓(𝑥) = 𝑚𝑥 + 𝑝. Se 𝑓 passa pelos
pontos 𝐴(0,4) e 𝐵(3,0), então 𝑓 −1 passa pelo ponto:
a) (8, -2)
b) (8, 3)
c) (8, -3)
d) (8, 2)
e) (8, 1)
8- Considere as funções reais dadas pelas leis:
a) 𝑓 (𝑥) = 𝑥
b) 𝑔 (𝑥) = 2𝑥
c) ℎ (𝑥) = 3𝑥
d) 𝑖 (𝑥) = 4𝑥
e) 𝑡 (𝑥) = 𝑥
f) 𝑦 (𝑥) = 𝑥 − 1
g) 𝑒 (𝑥) = 𝑥 − 3
h) 𝑢(𝑥) = 𝑥 + 3
i) 𝑤 (𝑥) = 𝑥 + 4
Em um mesmo plano cartesiano, construa os gráficos das funções dadas e os das respectivas
funções inversas.
Gabarito
1- 𝑓 −1 (x) =
2-
1−𝑥
5
3
a) 𝑓 −1 (𝑥) = √√𝑥
b) Os pontos (0,0) ; (1,1) ; (−1, −1)
3𝑥−9
a) 𝑓 −1 (𝑥) = 4
b) 𝑔−1 (𝑥) =
c) ℎ
−1
3−𝑥
2
= (𝑥) =
−2𝑥−1
14
d) 𝑚−1 (𝑥) = 3x − 5
3
e) 𝑛−1 (x) = √𝑥 − 1
f) 𝑝−1 (x) =
𝑥5
2
4a) 𝑓 −1 (𝑥) = −𝑥 + 3
𝑥
b) 𝑔−1 (𝑥) = 2
c) ℎ−1 𝑥) = 3𝑥 + 6
5- Letra C
6- Letra C
7- Letra C



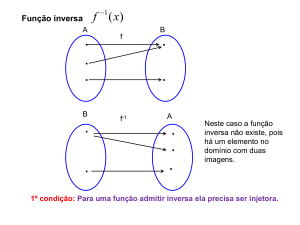

![Lista de Função Bijetora e Função Inversa Prof. Pinda [ ) ( ] { } { }0 { } { }](http://s1.studylibpt.com/store/data/004507856_1-44b04ad2f8f41c374310ce9def72d79e-300x300.png)