COLÉGIO PAULO VI

COLÉGIO PAULO VI
Ficha de Avaliação de Matemática
11 de Março de 2005
12º ano
Para cada uma das questões do grupo I seleccione a resposta correcta de entre as
alternativas que lhe são apresentadas e escreva na folha de teste a letra que
corresponde à sua opção.
Atenção! Se apresentar mais de uma resposta, ou resposta ambígua, a questão será
anulada.
Grupo I
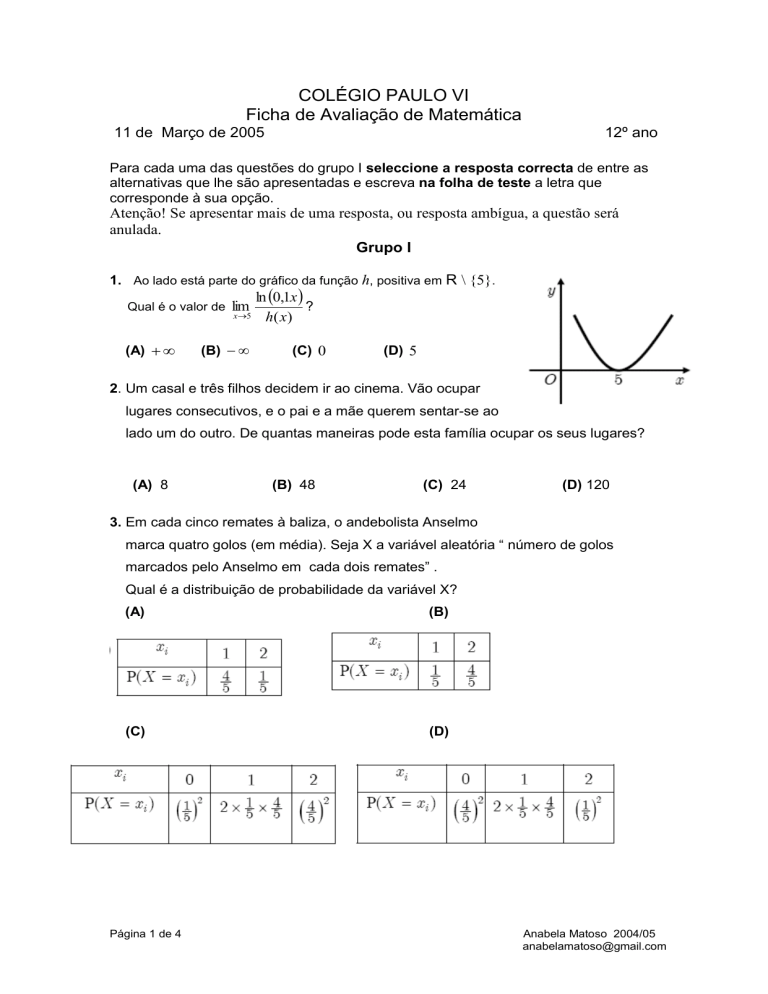
1. Ao lado está parte do gráfico da função h, positiva em R \ {5}.
Qual é o valor de
(A)  
ln 0,1x 
?
x5
h( x )
lim
(B)  
(C) 0
(D) 5
2. Um casal e três filhos decidem ir ao cinema. Vão ocupar
lugares consecutivos, e o pai e a mãe querem sentar-se ao
lado um do outro. De quantas maneiras pode esta família ocupar os seus lugares?
(A) 8
(B) 48
(C) 24
(D) 120
3. Em cada cinco remates à baliza, o andebolista Anselmo
marca quatro golos (em média). Seja X a variável aleatória “ número de golos
marcados pelo Anselmo em cada dois remates” .
Qual é a distribuição de probabilidade da variável X?
(A)
(B)
(C)
(D)
Página 1 de 4
Anabela Matoso 2004/05
[email protected]
4. Considere as seguintes afirmações:
(i)
(ii)
O gráfico de uma função de domínio R não tem assímptotas verticais.
O gráfico de uma função tem no máximo duas assímptotas não
verticais.
(iii)
O gráfico de uma função pode ter um número infinito de assímptotas
verticais.
(iv)
Se x  a é uma assímptota do gráfico de f então f pode ser contínua
em x  a .
Podemos afirmar que são falsas:
(A) (ii) e (iii)
(B) (i) e (iv)
(C) (i) e (ii)
(D) (ii) e (iv)
5. Na figura está desenhada parte da representação gráfica de
uma função f , cujo domínio é R \ 0. As rectas de
equações x  0 e y  3 são assímptotas do gráfico de f .
É dada a sucessão definida por xn  3  n 2 .
Qual o valor de lim f ( xn ) ?
(A) 3
(B) 0
(C)  
(D)  
6. Indica qual das seguintes expressões é, para qualquer número real a > 1, igual a
a 2+loga 3 .
(A) 2a3
(B) 3a2
(C) 3 + a2
(D) 2 + a3
7. De uma função f de domínio R  , sabe-se que a recta de equação y  2  x é
assímptota do seu gráfico. Qual é o valor de lim f ( x ) ?
x 
(A)  
Página 2 de 4
(B)  
(C) 2
(D)  1
Anabela Matoso 2004/05
[email protected]
Grupo II
Na resolução deste grupo deve apresentar todos os esquemas e cálculos que traduzam o seu
raciocínio e todas as justificações julgadas necessárias.
À excepção da questão 2.5) todas as questões devem ser resolvidas analiticamente,
recorrendo à calculadora apenas para efectuar eventuais cálculos numéricos.
Seja h a função real de variável real, de domínio R, definida por:
1.
e x  x
x2

.
h( x )  
x
x2
2 
x2

1.1 Estude a continuidade da função h.
1.2 Determine as assímptotas do gráfico de h .
1.3 Mostre, recorrendo ao Teorema de Bolzano, que a equação h( x) 
pelo menos uma solução no intervalo  3;2 .

1
5
, tem
2

 h( x ) 
1.4 Calcule, caso exista, lim 2  2
x 2 
x 4

Considere a função real de variável real definida por f ( x) 
2.
1
.
ln( x  1)
2.1 Determine o domínio da função f .
2.2 Determine os valores de x tais que
1
 2.
f ( x)
2.3 Considere a função g ( x)  e x  1 .
A equação f ( x)  g ( x) tem uma única solução. Utilizando a sua calculadora,
determine-a graficamente.
Apresente o resultado arredondado às décimas e explique como procedeu,
apresentando o gráfico, ou gráficos, obtidos na calculadora.
3.
Considere a função h , real de variável real da qual se sabe que:
lim h( x)  1 ;

x 





h é contínua em R \ 0;
h(2)  4
lim h( x)  
x 0
lim h( x)  1
x 0
lim h( x)  x   0
x
Esboce um possível gráfico para a função h , indicando o seu contradomínio.
Página 3 de 4
Anabela Matoso 2004/05
[email protected]
4.
Na figura está parte da representação gráfica da
f , de domínio
função
R  , definida por
f ( x)  ln x .
Os pontos A e C, que pertencem ao gráfico da
função f , são vértices de um rectângulo [ABCD],
de lados paralelos aos eixos do referencial.
As abcissas de A e de C são 2 e 6, respectivamente.
Mostre que a área do rectângulo [ABCD] é dada por Área  ln( 81)
5.
5.
O código de um certo alarme para habitações é uma sequência de 4 algarismos,
como por exemplo 0477.
5.1 Quantos códigos diferentes existem:
5.1.1
com exactamente dois cincos?
5.1.2
pares e cujo número representado esteja entre 4000 e 7000?
5.2 O Sr. Manuel mandou instalar um alarme na sua moradia e escolheu um
código.
Qual a probabilidade de que o código escolhido pelo Sr. Manuel tenha
quatro algarismos iguais?
FORMULÁRIO
Limites notáveis:
ln( x  1)
ex 1
lim
1
lim
1
x

0
x 0
x
x
ex
lim p   ( p  IR )
x  x
senx
1
x 0
x
ln x
lim
0
x   x
lim
FIM
Questão 1.
Cotação 9
Questão 1.1
Cotação 16
Página 4 de 4
2.
9
1.2
14
3.
9
1.3
13
1.4
10
4.
9
2.1
10
2.2
10
5.
9
2.3
16
6.
9
7.
9
Grupo I
63 pontos
3. 4. 5.1.1 5.1.2 5.2
14 10 6
10
8
Grupo II
137 pontos
Anabela Matoso 2004/05
[email protected]