Teste_Marco_turmaA-v1

COLÉGIO PAULO VI
Teste 4 (12ºA)
Matemática A
Duração do Teste: 90 minutos 30.03.2011
12.º Ano de Escolaridade
______________________________________________________________________
Teste de Matemática A – 12.º Ano – Página 1
______________________________________________________________________
Teste de Matemática A – 12.º Ano – Página 2
1. Considera as seguintes afirmações:
(i) O gráfico de uma função de domínio R não admite assímptotas verticais.
(ii) Se a é um zero da derivada de uma dada função g então a função g admite
para x  a um máximo ou um mínimo relativos.
(iii) Se h é contínua em x  a então existe h (a )
Podemos afirmar que:
(A) as afirmações são todas verdadeiras
(B) as afirmações são todas falsas
(C) só as afirmações (i) e (ii) são verdadeiras
(D) só as afirmações (ii) e (iii) são falsas
2. Sejam X e Y dois acontecimentos independentes de uma mesma experiência aleatória.
Se P ( X )  0, 7 e
(A)
3
5
P( X Y )  0,1 , então o valor de P(Y ) é:
(B)
1
5
(C)
2
3
(D)
4
7
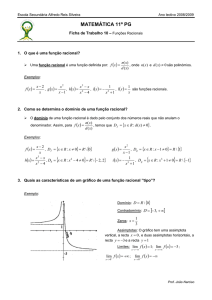
3. Na figura estão representadas parte do gráfico de uma
função h , de domínio R \ 0 e a recta t, assímptota do

gráfico de h e tangente ao seu gráfico no ponto de
abcissa  1 . Qual é a proposição verdadeira?
(A) h  1  lim h( x)
x0
(B) h 1  lim h( x)
x  
(C) h  1  lim
h( x )
x 0
x
h( x )
(D) h  1  lim
x  
x
4. O conjunto-solução da condição
log 2 (6x  5)  log 2 x  0 é:


1
6
(A)  1, 
(B)

1 
6
(C)  
 5 
,0
 6 
(D) 
______________________________________________________________________
Teste de Matemática A – 12.º Ano – Página 3
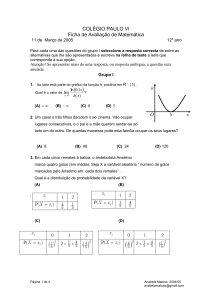
5. Ao lado está desenhada parte do gráfico da função f´, primeira
derivada de uma função f.
Em qual das figuras seguintes poderá estar parte da
representação gráfica da função f ?
(A)
(B)
(C)
(D)
1.
O frigorífico da Clarinda tem seis prateleiras e na porta tem um compartimento de dezoito
lugares para colocar ovos.
1.1 A Clarinda comprou 6 ovos de pata e 4 ovos de galinha e reparou que os de
pata têm casca de cor branca enquanto que a casca dos de galinha é
acastanhada. Supondo que a Clarinda tem que arrumar os dez ovos no
compartimento quantas são as disposições possíveis?
1.2 Para uma melhor organização dos alimentos, ela tem de colocá-los de uma
certa maneira: legumes, lacticínios, carne e peixe, cada grupo numa prateleira
diferente.
Sendo a colocação dos quatro grupos de alimentos nas seis prateleiras feita
ao acaso, qual é a probabilidade de os legumes ficarem na prateleira de baixo,
não ficando nada na prateleira do topo?
Apresente o resultado em percentagem arredondado às décimas.
______________________________________________________________________
Teste de Matemática A – 12.º Ano – Página 4
2.
e x ( x  1) se x  0

Considere a função f de domínio IR definida por f ( x)  
ln x
se x  0
x 
x

Usando processos exclusivamente analíticos:
2.1 Estude a função f quanto à continuidade em
x  0 e, de acordo com o resultado obtido,
diga o que pode concluir quanto à derivabilidade da função f em
x  0.
2.2 Estude a função f quanto à existência de assímptotas do seu gráfico.
2.3 Considere os seguintes pontos:

O ponto A cuja abcissa é o zero de f ;

O ponto B, do primeiro quadrante, cuja ordenada é um mínimo relativo da função
f;

O ponto O, origem do referencial.
Recorrendo às capacidades gráficas da calculadora determine a área do triângulo
[AOB].
Explique o seu raciocínio numa pequena composição.
Apresente um esboço do(s) gráfico(s)
em que
baseou a sua resposta, indicando as
coordenadas dos pontos relevantes.
3.
Considere a função real de variável real definida por
g ( x)  2 x  e1 x .
Usando processos exclusivamente analíticos:
3.1 Estude g quanto à monotonia e existência de extremos relativos.
3.2 Mostre que a equação da recta tangente ao gráfico de g que é paralela à bissectriz dos
quadrantes pares tem de equação reduzida
 e6 
y   x  ln   .
 27 
3.3 Mostre que o gráfico de g intersecta a recta de equação y   x  4 num ponto de abcissa
pertencente ao intervalo
4.
0,2 .
De uma função, real de variável real, g, sabe-se que:




3 é um zero
lim g ( x)  2
x 1
A recta de equação
x  1é assímptota do gráfico de g.
lim g ( x)  x  2  0
x

Não existe g´(2) mas g é contínua em

g´(1)  0
x  2
Esboce uma possível representação gráfica para a função g e, de acordo, com o seu
esboço, indique o número de soluções da equação g ( x )  1 .
FIM
______________________________________________________________________
Teste de Matemática A – 12.º Ano – Página 5
COTAÇÕES
Grupo I ……………………………..(5 x 10 pontos) ……………… 50 pontos
Grupo II…………………………………………………………………150 pontos
1. …………………………………………………………………..30 pontos
1.1. ……………………………………………….15 pontos
1.2 …………………………………………….….15 pontos
2. …………………………………………………………………….50 pontos
2.1. ……………………………………………….15 pontos
2.2 ……………………………………………… 20 pontos
2.3 ……………………………………………… 15 pontos
3. …………………………………………………………………….55 pontos
3.1. ………………………………………………..20 pontos
3.2 ………………………………………………..20 pontos
3.3 ………………………………………………..15 pontos
4. …………………………………………………………………….15 pontos
Total …………………………………………………………………… 200 pontos
______________________________________________________________________
Teste de Matemática A – 12.º Ano – Página 6