ficha

COLÉGIO PAULO VI
Ficha de Avaliação de Matemática
5 de Fevereiro de 2004
12º ano
Comece por escrever na folha de teste : versão B
Para cada uma das questões do grupo I seleccione a resposta correcta de entre as
alternativas que lhe são apresentadas e escreva na folha de teste a letra que
corresponde à sua opção.
Atenção! Se apresentar mais de uma resposta, ou resposta ambígua, a questão será
anulada.
Grupo I
1. Qual das seguintes expressões é, para qualquer número real positivo a ,
igual a
e3ln a ?
(A) 3 + a
(B) 3a
3
(C) a
(D) 3a
2. Considere a função f definida por f ( x ) = ln(3 x )
( ln designa logaritmo de base e)
Qual dos seguintes pontos pertence ao gráfico da função f ?
(A) (e,1 + ln 3)
(B) (e, ln 3)
(C) (e, e ln 3)
(D) (e, e + ln 3)
3. Seja h a função de expressão analítica h( x) = log(1 − 2 x ) .
O domínio de h é:
(A) R −
(B) R0−
(C) R +
(D) R0+
4. Numa tômbola de beneficência fizeram-se 1000 rifas e colocaram-se 20
prémios a concurso. Qual a probabilidade de, comprando 3 rifas, serem duas
premiadas?
(A)
3
166167000
(B)
931
830835
(C)
3
50
(D)
1
25
5. Quantos números de quatro algarismos diferentes existem entre 1000 e
4000?
(A) 2325
Anabela Matoso
(B) 3600
(C) 3014
Página 1
(D) 1792
30-01-2006
versão B
6. Sabendo que, na figura, cada quadrado tem metade do lado do anterior e
supondo que desta forma podemos construir um números infinito de
quadrados, então a soma de todos os perímetros é:
10
(A) 10
(B) 20
(C) 40
(D) 80
7. Considera as seguintes sucessões:
2
2n
n
⎛ n + 1⎞
⎛ 1⎞
⎛ 1⎞
u n = ⎜1 + ⎟ ; v n = ⎜
⎟ e wn = ⎜1 + ⎟ .
⎝ n ⎠
⎝ 2⎠
⎝ n⎠
Sendo u = lim u n , v = lim v n e w = lim wn podemos afirmar que:
(A) u = 1 ;
v = e2
(C) u = +∞
; v = e2
Anabela Matoso
e w = +∞
(B) u = 1 ;
v = +∞ e w = 0
e w=e
(D) u = 1 ;
v = e2
Página 2
e w=e
30-01-2006
Grupo II
Na resolução deste grupo deve apresentar todos os esquemas e cálculos que
traduzam o seu raciocínio e todas as justificações julgadas necessárias.
Sempre que não se indicar a aproximação pretendida deve ser indicado o valor
exacto.
1. A pressão atmosférica de cada local da Terra depende da altitude a que
este se encontra.
Admita que a pressão atmosférica (medida em quilopascal) é dada, em
função da altitude h (em quilómetros), por
P( h ) = 101 × e −0,12 h
1.1 A montanha mais alta de Portugal é o Pico, na ilha do Pico – Açores.
A altitude do cume do Pico é 2350 metros.
Qual é o valor da pressão atmosférica nesse local? Apresente o
resultado em quilopascal, arredondado às unidades.
1.2 Determine x tal que, para qualquer h , P (h + x ) =
1
P (h ) . Apresente o
2
resultado arredondado às décimas.
Interprete o resultado no contexto do problema.
2. O nível de som provocado por uma onda sonora de intensidade x é dado
por:
⎛ x ⎞
D ( x ) = 10 log10 ⎜ −10 ⎟ , em que D ( x ) são decibéis e x são hertz ( x > 0) .
⎝ 10 ⎠
2.1 Mostre que D ( x ) = 100 + 10 log10 x , para qualquer x > 0 .
2.2 Qual o nível de som provocado por uma onda sonora de intensidade
10 −3 hertz?
2.3 Determine a intensidade de uma onda sonora que provoca um nível
de som de 80 decibéis.
3. Considere a função real de variável real definida por:
g ( x ) = 1 − ln( e − x )
3.1 Determine o domínio de g .
3.2 Averigua se a função tem zeros.
3.3 Determine, sob a forma de intervalos de números reais, o
conjunto solução da condição g ( x ) ≥ 1 − ln( 3e) .
3.4 Caracterize a função inversa de g .
Anabela Matoso
Página 3
30-01-2006
4. Calcule, caso existam cada um dos seguintes limites:
4.1 lim+
2x − 3
x −1
4.2 lim
2x − 3
x2 −1
x → −1
x → −1
x2 + x3 − 3
4.3 lim
x → +∞
2x3 + x
4.4 lim
x →+∞
(x
2
+ 3x − x
)
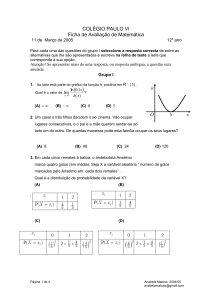
5. Na figura está parte da
representação gráfica da função h .
Indique, caso existam, os seguintes limites:
5.1 lim− h ( x )
x →1
5.2 lim h ( x )
x→1
5.3
5.4
5.5
5.6
lim h ( x )
x → −∞
lim h ( x )
x → +∞
1
h( x )
−2
lim
x →−∞ h ( x )
lim
x → −2 +
( Apenas se pretende a indicação do valor do limite, caso exista, ou que
escreva não existe, se esse for o caso.)
FIM
Anabela Matoso
Página 4
30-01-2006