Funcoes Racionais 1 - Escola Secundária de Alves Redol

Escola Secundária de Alves Redol de Vila Franca de Xira
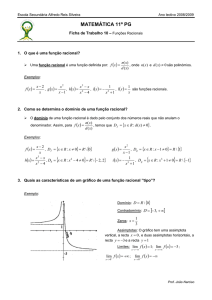
Disciplina de Matemática A – 11º Ano – Tema: Funções Racionais
1. Consideremos as seguintes afirmações:
I – A função
é decrescente.
II – A função
é uma função ímpar.
III – O gráfico da função
IV – A função
é simétrico relativamente ao eixo das abcissas.
tem duas assímptotas.
Qual ou quais são verdadeiras?
2. A equação da assímptota horizontal da função
(A)
(B)
3. A respeito da função
assim definida: ( )
4. Considere a função ( )
5. Seja ( )
é:
(C)
I – Assímptota horizontal do gráfico:
( )
II –
III – Assímptota vertical do gráfico:
( )
IV Qual ou quais são verdadeiras?
(A) Só a I, a II e a IV.
(B) Só a I e a III.
de equação:
(A)
definida por ( )
(D)
considere as seguintes afirmações.
(C) Só a II.
(D) As quatro.
A assímptota ou assímptotas verticais do gráfico da função são as rectas
(C)
(B)
Sabendo que ( )
(D)
tem-se:
(A)
(B)
(C)
(D)
( )
6. Sabe-se que
Com esta informação, o que se pode concluir?
(A) A recta de equação
é uma (B) A recta de equação
assímptota.
assímptota.
(C) A recta de equação
assímptota.
é uma (D) A recta de equação
assímptota.
é uma
é uma
Escola Secundária de Alves Redol de Vila Franca de Xira
Disciplina de Matemática A – 11º Ano – Tema: Funções Racionais
( )
7. Sabe-se que
8. Para um certo valor de
Qual dos seguintes pode ser o gráfico da função
e para um certo valor de
a expressão ( )
define a função
cujo gráfico
está parcialmente representado na figura.
Qual das afirmações seguintes é verdadeira?
(A)
(B)
(C)
(D)
9. O gráfico da função f, representada na figura , tem por assímptotas as rectas x  1 e y  2 . Qual das
expressões analíticas pode definir f x  ?
(A) f x   2 
(C) f x  
2x
x 1
2
x 1
(B) f x  
 2x
x 1
(D) f x  
x
x 1
Prof. Vânia Santos
Escola Secundária de Alves Redol de Vila Franca de Xira
Disciplina de Matemática A – 11º Ano – Tema: Funções Racionais
10. Sabendo que o gráfico de uma função f admite as rectas x  3 e y  2 como únicas assímptotas, então o gráfico
da função definida por g x   2  f x  3 admite como assímptotas:
(A) x  3 e y  2
(B) x  6 e y  4
11. Considere a função definida por g ( x) 
(A)
(B)
{
(C) x  6 e y  0
(D) x  0 e y  4
x4
. Podemos afirmar que o domínio da função é:
x2 1
}
(C)
{ }
(D)
{
}
12. A figura representa o gráfico de uma função real de variável real f.
12.1. Indique qual a afirmação correcta:
(A) lim f (x)  3 e lim f (x)  
(B) lim f (x)  3 e lim f (x)  
(C) lim f (x)  1 e lim f ( x)  3
(D) lim f (x)  3 e lim f (x)  
x 
x 
x 1
x 1
x 
x 
x 1
x 1
12.2. Considere a função h definida por h(x)  f (x -2)  1 . As assimptotas do gráfico de h são as rectas de
equação:
(A) x=-1 e y=3
(C) x=-3 e y=4
(B) x=1 e y=4
(D) x=0 e y=5
Prof. Vânia Santos
Prof. Vânia Santos