)( )( α απ α cotg cotg cotg −= − =− α απ 2π π π π π

59
Capítulo II: Funções Reais de Variável Real___________________________
Função co-tangente
(0,1)
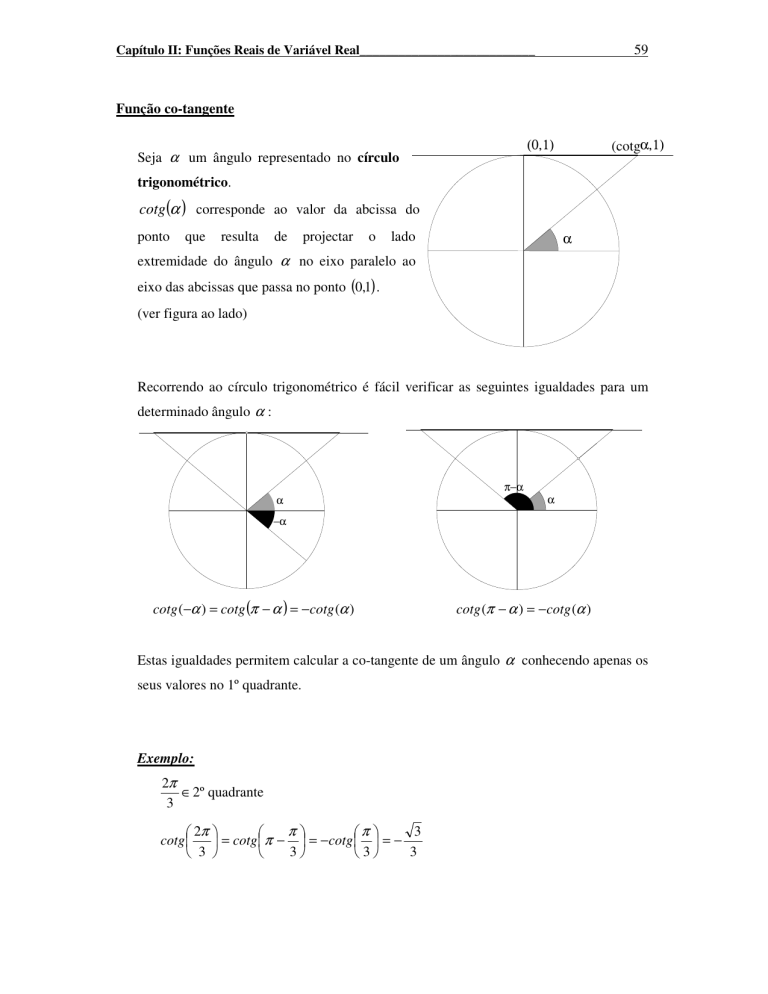
Seja α um ângulo representado no círculo
(cotgα,1)
trigonométrico.
cotg (α ) corresponde ao valor da abcissa do
ponto
que
resulta
de
projectar
o
lado
α
extremidade do ângulo α no eixo paralelo ao
eixo das abcissas que passa no ponto (0,1) .
(ver figura ao lado)
Recorrendo ao círculo trigonométrico é fácil verificar as seguintes igualdades para um
determinado ângulo α :
α
π−α
α
−α
cotg (−α ) = cotg (π − α ) = −cotg (α )
cotg (π − α ) = −cotg (α )
Estas igualdades permitem calcular a co-tangente de um ângulo α conhecendo apenas os
seus valores no 1º quadrante.
Exemplo:
2π
∈ 2º quadrante
3
cotg
2π
π
π
3
= cotg π −
= −cotg
=−
3
3
3
3
Capítulo II: Funções Reais de Variável Real___________________________
60
Como função real de variável real, temos
f : IR \ {kπ , k ∈ Ζ} →
IR
x
cotg ( x)
À função f dá-se o nome de função co-tangente.
(obs: x é a medida de um ângulo em radianos)
O seu gráfico é
Características desta função:
•
Domínio: IR \ {kπ , k ∈ Ζ};
•
Contradomínio: IR;
•
Injectividade: não injectiva;
•
Zeros: x =
•
Paridade: ∀x cotg (− x) = −cotg ( x)
(co-tangente é uma função ímpar);
•
Periodicidade: ∀x cotg ( x + π ) = cotg ( x)
( π é o período positivo mínimo);
•
Limitada: não limitada;
•
Máximos: não tem;
•
Mínimos: não tem.
π
2
+ kπ , k ∈ Z ;
Capítulo II: Funções Reais de Variável Real___________________________
61
Função arco co-tangente
Consideremos a função
f : IR \ {kπ , k ∈ Ζ} →
IR
x
cotg ( x)
Esta função não é injectiva.
Por exemplo, há infinitos pontos do domínio que têm por imagem zero
( cotg ( x ) = 0 ⇔
x=
π
2
+ kπ , k ∈ Z ). Pelo que f não admite inversa.
Contudo, podemos considerar uma restrição do domínio onde a função co-tangente seja
injectiva (chamada restrição principal):
g:
]0, π [
x
→
IR
cotg ( x)
cujo gráfico é:
Assim definida, g é uma função injectiva e portanto faz sentido falar na sua inversa,
g −1 .
Então g −1 tem por domínio IR , imagem ]0, π [ e a cada x ∈ IR faz corresponder o
ângulo (ou arco) cuja co-tangente é x , que se representa por arccotg ( x ) .
62
Capítulo II: Funções Reais de Variável Real___________________________
]0, π [
g −1 : IR →
arccotg ( x)
x
cujo gráfico é
y
π
π/2
x
Características desta função:
•
Domínio: IR ;
•
Contradomínio: ]0, π [ ;
•
Injectividade: injectiva;
•
Zeros não tem;
•
Paridade: não é par nem é ímpar;
•
Monotonia: estritamente decrescente;
•
Limitada: ∀x
•
Máximos: não tem;
•
Mínimos: não tem;
0 < arccotg ( x) < π ;
Obs.:
•
O arccotg ( x) é o valor real y tal que cotg ( y ) = x , onde x ∈ IR , ou seja:
arccotg ( x) = y ⇔ cotg ( y ) = x
•
cotg (arccotg ( x )) = x
onde x ∈ IR ;
•
arccotg (cotg ( x )) = x
onde 0 < x < π .
63
Capítulo II: Funções Reais de Variável Real___________________________
Exemplos:
•
cotg arcccotg
•
arcccotg cotg
•
arcccotg cotg
1
7
1
7
=
π
=
6
7π
6
π
6
= arccotg cotg π +
π
6
= arccotg cotg
π
6
=
π
pois
6
7π
∉ ]0, π [ .
6
Exercício:
1
2
Considere a função definida por f ( x) = arccotg (x + 3) −
π
4
.
Determine o domínio e contradomínio de f. Caracterize a inversa, caso exista.
Resolução:
D f = IR . Determinemos o contradomínio de f :
0 < arccotg ( x + 3) < π
Logo Im( f ) = −
⇔ 0<
π π
1
π
arccotg ( x + 3) <
2
2
⇔ −
π
4
< f (x ) <
.
,
4 4
f é uma função injectiva porque é composta de funções injectivas.
Determinemos a expressão analítica da inversa:
f ( x) = y
⇔
⇔
⇔
1
π
arccotg (x + 3) − = y
2
4
π
arccotg (x + 3) = 2 y +
2
π
x + 3 = cotg 2 y +
⇔
2
x = cotg 2 y +
Portanto
f
−1
:
−
π π
,
4 4
x
→
IR
cotg 2 x +
π
2
−3
π
2
−3
π
2
−
π
4
=
π
4
Capítulo II: Funções Reais de Variável Real___________________________
Função secante
A função secante define-se como
f : IR \
π
2
+ kπ , k ∈ Z
→
IR
sec( x) =
x
1
cos( x)
O seu gráfico é:
Características desta função:
•
Domínio: {x ∈ IR : cos( x) ≠ 0} = IR \
•
Contradomínio: IR \ [− 1,1] ;
π
2
+ kπ , k ∈ Ζ ;
Se x ∈ Dsec , temos − 1 ≤ cos( x ) < 0
∨ 0 < cos( x) ≤ 1
logo,
1
1
≥
− 1 cos( x)
∨
1
1
≥
cos( x) 1
ou seja,
sec( x) ≤ −1 ∨ sec( x) ≥ 1
∴ sec(x) ∈ ]− ∞,−1] ∪ [1, ∞[
64
Capítulo II: Funções Reais de Variável Real___________________________
•
Injectividade: não injectiva;
•
Zeros: não tem;
•
Paridade: ∀x
•
Periodicidade ∀x sec( x + 2π ) =
sec(− x ) =
1
1
=
= sec( x)
cos( − x ) cos( x )
65
(secante é uma função par);
1
1
=
= sec( x )
cos( x + 2π ) cos( x )
( π é o período mínimo positivo)
•
Limitada: não limitada;
•
Máximo: em x = π + 2kπ , k ∈ Z ;
•
Mínimo: em x = 2kπ , k ∈ Z ;
Obs.:
Os máximos e mínimos referidos nas características da função secante são
relativos. No entanto, a função secante não tem extremos absolutos.
Exercício:
Considere a função definida por f ( x ) =
1
cos x +
π
+ 2.
6
Determine o domínio e o contradomínio. (Sugestão: esboce o gráfico de f usando as
transformações descritas nas páginas 26-30)
Caracterize a inversa da função f na restrição x ∈ − π , 5π \ 2π .
6 6
3
Capítulo II: Funções Reais de Variável Real___________________________
Função co-secante
A função co-secante define-se como
f : IR \ {kπ , k ∈ Z} →
IR
cos ec( x) =
x
1
sen( x)
O seu gráfico é:
Características desta função:
•
Domínio: {x ∈ IR : sen( x) ≠ 0} = IR \ {kπ , k ∈ Ζ};
•
Contradomínio: ]− ∞,−1] ∪ [1,+∞[
•
Injectividade: não injectiva;
•
Zeros: não tem;
•
Paridade: ∀x
co sec(− x ) =
1
1
=
= −co sec( x )
sen( − x ) − sen( x )
(co-secante é uma função ímpar);
•
Periodicidade: ∀x
co sec( x + 2π ) =
1
1
=
= co sec( x)
sen( x + 2π ) sen( x)
( π é o período mínimo positivo)
•
Limitada: não limitada;
•
Máximos: em x = −
π
2
+ 2kπ , k ∈ Z ;
66
Capítulo II: Funções Reais de Variável Real___________________________
•
Mínimos: em x =
π
2
67
+ 2kπ , k ∈ Z ;
Obs.:
Os máximos e mínimos referidos nas características da função co-secante são
relativos. No entanto, a função secante não tem extremos absolutos.
Exercício:
Considere a função definida por f ( x ) = cos ec x −
π
3
. Determine o domínio e o
contradomínio.
Caracterize a inversa da função f na restrição x ∈ − π , 5π \ π .
6 6
3