A tangente no ciclo trigonométrico
Matemática 2
Aulas 10 e 11
Prof. Figo
Inicialmente definimos a função tangente como sendo o quociente entre os
catetos oposto e adjacente em relação ao ângulo interno (agudo) de um
triângulo retângulo. No âmbito do ciclo trigonométrico usaremos o mesmo
conceito, todavia sua estrutura permite extender o conceito da tangente
para ângulos maiores do que 90°.
sen 𝜃
tg 𝜃 =
cos 𝜃
A função tangente
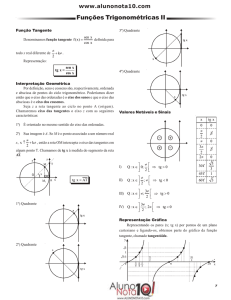
Considere o ciclo trigonométrico abaixo, o qual apresenta uma
reta tangente no ponto que consideramos (desde o início) a
origem das medidas dos arcos, isto é, o ponto 𝐴(1; 0)
Algebricamente a tangente de um ângulo 𝛼 é definida como
sendo o comprimento do segmento 𝐴𝐵, o qual poderá ser zero,
positivo ou negativo. Evidentemente, o sinal da tangente
depende da orientação que tomamos para o seu cálculo. Como a
mesma é medida na vertical, teremos que os valores medidos
acima do zero serão considerados positivos. Os valores medidos
abaixo do zero serão tomados como negativos.
Tangente dos ângulos notáveis e seus
múltiplos
Variação do sinal da função tangente
A função cotangente
A cotangente de um ângulo é definida como sendo o
inverso de sua tangente, ou seja, se 𝜃 é um arco do ciclo
trigonométrico, temos que
1
cotg 𝜃 =
tg 𝜃
se n 𝜃
Como tg 𝜃 = cos 𝜃 , segue que cotg 𝜃 =
cotg 𝜃 =
cos 𝜃
sen 𝜃
1
se n 𝜃
cos 𝜃
, ou seja:
Para quais ângulos 𝜃 a cotangente não está definida?
Observando a relação cotg 𝜃 =
cos 𝜃
sen 𝜃
, concluímos que, se sen 𝜃 = 0, sua
cotangente não existe. Ilustremos com alguns exemplos:
𝜃 = 0 , 𝜃 = 𝜋 , 𝜃 = 2𝜋 𝜃 = 3𝜋, etc.
De modo geral, se 𝜃 = 𝑘𝜋, 𝑘 ∈ ℤ, temos que ∄ cotg 𝜃
Interpretação geométrica da cotangente
Outras relações trigonométricas
Definimos como a secante de um ângulo 𝜃 o inverso de
seu cosseno, isto é:
sec 𝜃 =
1
cos 𝜃
, onde cos 𝜃 ≠ 0.
Para o seno não ficar “sozinho” nesse conceito, definimos a
cossecante de um ângulo 𝜃 como sendo o inverso de seu
seno, isto é:
1
cossec 𝜃 = se n 𝜃 , onde sen 𝜃 ≠ 0.