trigonometria-i

TRIGONOMETRIA-I
1- Razões Trigonométricas
Seno =
cateto oposto
hipotenusa
cateto adjacente
hipotenusa
cateto oposto
Tangente =
cateto adjacente
Cosseno =
b
a
c
cos B =
a
sen B =
tg B =
b
c
2- Arcos Notáveis
30º
Seno
45º
1
2
2
Cosseno
3
2
3
2
1
2
2
Tangente
60º
2
2
1
3
3
3
3- Relação entre as unidades
Grau
Grado
Radiano
90º
100 gr
/2
180º
200 gr

270º
300 gr
3/2
360º
400 gr
2
4- Comprimento de um arco de circunferência
=
s
r
 = ângulo
s = comprimento do arco
r = raio
5- Circunferência trigonométrica
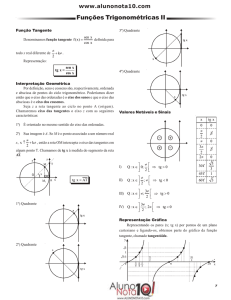
6- Arcos trigonométricos
- São arcos de uma circunferência trigonométrica com mesma origem e mesma extremidade.
Os arcos trigonométricos podem ser:
sen C =
cos C =
tg C =
 Positivos, quando marcados no sentido anti-horário.
 Negativos, quando marcados no sentido horário.
 Maiores que 360º ou 2 rad, quando têm mais de uma volta.
7- Arcos côngruos
Dois arcos são côngruos quando têm a mesma extremidade e diferem apenas pelo número de voltas inteiras.
º + k . 360º
 + 2k
FUNÇÕES CIRCULARES
I- Estuda da Função Seno
1- Definição
- Dado um arco AM, de medida x radianos, definimos como seno x a ordenada do ponto M e representamos sen x =
OM 2
y = sen x
2- Gráfico
 D=R
 Im = [-1, +1], isto é 1  sen x  1
2
 p=
 p = 2
k
 Sen x = – sen (– x) é uma função ímpar
II- Estudo da Função Cosseno
1- Definição
- Dado um arco AM, de medida x radianos, definimos como cosseno x a abscissa do ponto M e representamos cos x
= OM 1
y = cos x
2- Gráfico
 D=R
 Im = [-1, +1], isto é 1  cos x  1
2
 p=
 p = 2
k
 cos x = cos (– x) é uma função par
III- Estudo da Função Tangente :
1- Definição
- Dado um arco AM, de medida x radianos, com x 

+ k, definimos como tangente de x a medida algébrica do
2
segmento AT e representamos tg x = AT .
y = tg x
tg x =
sen x
cos x
2- gráfico

+ k, k  Z}
2

D = {x  R / x 

Im = ]- , +[

p=

tg x = - tg (- x) é uma função ímpar

p=
k
IV- Estudo da Função Cotangente
1- Definição
- Dado um arco AM, de medida x radianos, com x 

+ k, definimos como cotangente de x a medida algébrica
2
do segmento BT e representamos tg x = BT .
y = cotg x
cotg x =
cos x
sen x
2- Gráfico
 D = {x  R / x  k, k  Z}
 Im = ]- , +[
 p=

p=
k
 cotg x = - cotg (- x) é uma função ímpar
V- Estudo das Funções Secante e Cossecante
1- Definições
- Consideremos um número real x que tem imagem num ponto P do ciclo, tal que a reta tangente ao ciclo em P
intercepta o eixo dos cossenos em S e o eixo dos senos em S’.
Chamamos secante de à medida algébrica de OS cossecante de x à de OS' . Indicamos:
sec x = OS
e
cossec x = OS'
1
cos x
1
cossec x =
sen x
sec x =
2- Gráficos
2.1- Função secante: y = sec x

+ k, k  Z}
2

D = {x  R / x 

Im = {y  R/ y  - 1 ou y  1}

p=
2
 p = 2
k
2.2- Função cossecante: y = cossec x
 D = {x  R / x  k, k  Z}
 Im = { y  R/ y  - 1 ou y  1}
2
 p=
 p = 2
k