Escola de Educação Básica Professora Maria Solange Lopes de

Ministério da Educação
Secretaria de Educação Profissional e Tecnológica
Instituto Federal Catarinense - Campus Sombrio
Curso de Licenciatura em Matemática
PLANO DE AULA
Dados de identificação
Escola: Escola de Educação Básica Professora Maria Solange Lopes de Borba
Município: São João do Sul, SC.
Disciplina: Matemática
Série/Ano: 3º
Turma: 301
Professor: Suzana Scandolara Selau
Níveis: Ensino Médio
Período: Vespertino
Tempo prevista: 10horas/aulas.
1. Temas: Números Complexos.
1.1.Subtemas: Números Complexos: Historicização; Retomando: conjuntos numéricos;
Conjunto dos números complexos: forma algébrica; Conjugado de um número
complexo; Operações com números complexos; Representação geométrica de um
número complexo; Módulo de um número complexo; Argumento de um número
complexo; A forma trigonométrica de um número complexo; Operações na forma
trigonométrica de um número complexo Teorema de De Moivre; Exercícios.
1.2. Justificativa:
A importância dos números complexos está marcada pelas suas múltiplas aplicações em
diversas áreas (Matemática, Física, Engenharia, Tecnologia,...). Números Complexos
introduzem-se para dar sentido à raiz quadrada de números negativos. Abre-se assim a porta a
um curioso e surpreendente mundo em que todas as operações (exceto a divisão por zero) são
possíveis.
Desta forma, se faz necessário aprender a expressão dos números complexos, a sua
representação gráfica, operações e forma trigonométrica/geométrica para facilitar sua
compreensão.
2. Objetivos:
 Identificar um número complexo;
 Distinguir parte real e imaginária de um número complexo;
 Operar com números complexos;
 Representar números complexos na sua forma trigonométrica.
3. Conteúdos envolvidos (conteúdos pré-requisitos para o desenvolvimento da aula).
 As operações básicas;
 Conjuntos numéricos;
 Plano cartesiano;
4. Estratégias:
4.1. Recursos: quadro, caneta para quadro, multimídia, maquete, EVA.
4.2. Técnicas: Aula expositiva e dialogada, atividades em sala de aula.
5. Procedimentos:
5.1. Problematização
Na maquete da cidade Triangonópolis apresentada na figura 01 a seguir, estão
destacados os pontos de A até N1, como fazer a representação algébrica destes, no plano de
Argand-Gauss, sendo que o eixo x representa o eixo real e o eixo y representa o eixo
imaginário. Como fazer a representação na forma trigonométrica? Que elementos são
necessários para tal representação?
Figura 01: Maquete da cidade Triangonópolis
Fonte: Elaborado pela autora
5.2. Historicização:
O conceito de número complexo se desenvolveu gradativamente, como ocorreu com os
demais tipos de números. Algumas equações do 2° grau, como x² + 1 = 0 não haviam solução
até o século XVI, pois para os matemáticos da época a raiz negativa não existia. Porém, não
foi este o motivo pelo qual os números complexos surgiram. Ao passar dos anos, alguns
matemáticos viram o mesmo problema para equações do 3º grau, onde percebeu-se que os
números reais não eram suficientes para resolver este tipo de equação.
Curiosidade: os números complexos surgiram na época do Renascimento, onde a
Europa estava se recuperando da peste negra e tinha uma forte influência do Humanismo. A
matemática grega não era compreendida, pois poucos sabiam ler grego e era um assunto
complexo. Assim, os europeus acabaram seguindo para outros ramos e continuaram a difundir
a Matemática.
Para resolver este problema, alguns matemáticos europeus, principalmente italianos
desenvolveram pesquisas, e houve algumas disputas. Antes das lutas, os números complexos
começaram a serem desenvolvidos por Scipione Dal Ferro. Ferro desenvolveu uma teria para
a solução das equações do tipo x³ + px + q = 0, mas acabou não publicando sua teoria.
Porque os matemáticos não divulgavam suas teorias? Nesta época os matemáticos
tinham costume de desafiar outros matemáticos, para se mostrar algumas vezes mais
inteligentes. Outra hipótese seria o medo de outro matemático encontrar algum erro na
fórmula, e assim surgiram alguns problemas sobre a notoriedade de algumas teorias. Antonio
Maria Fior conheceu a teoria de Ferro e ampliou para as equações do tipo x³ + px² + q = 0.
Fior acabou desafiando o jovem Niccolò Fontana, conhecido como Tartaglia a resolver
equações de grau 3. Para a surpresa de Fior, Tartaglia conseguiu resolver. Com muita
dedicação e esforço, Tartaglia procurou um método para a resolução destas equações e acabou
encontrando. Por este motivo, ele acabou vencendo todas as disputas com Fior.
Neste momento, chega aos ouvidos de Girolamo Cardano que Tartaglia sabia resolver
tal tipo de equação. Cardano implorou a “fórmula” para resolver estas equações. Tartaglia
recusou e acabou sendo acusado de mesquinho e egoísta. Com a insistência de Cardano e
jurando que não divulgaria o resultado, Tartaglia revelou a solução. Porém, Cardano não
cumpriu com sua palavra, e em 1545 fez a publicação num livro. Ele somente fez uma
menção de Tartaglia na sua obra e até hoje a fórmula é conhecida como “Fórmula de
Cardano”. Esta descoberta foi tão inusitada que ficou conhecida como o início da matemática
moderna.
Após esta “luta” surge um problema inquietante que Cardano trouxe conhecido na
época como números “sofisticados”, ou seja, as raízes quadradas de números
negativos. Cardano concluiu que estas raízes seriam um número “tão sutil quando inútil”. Ao
passar dos anos seria provado que estes números não eram inúteis como Cardano achava.
Mas, como resolver o problema dos números “sofisticados”? O que fazer com estes números?
Fica evidente que os números reais não eram suficientes para resolver este tipo de equação.
Assim, seguiram a mesma ideia que os pitagóricos seguiram quando descobriram o número
raiz quadrada de 2. Neste momento da história, se introduz a ideia de aceitar o imaginário, e
não somente o real.
Rafael Bombelli surge para trabalhar com este problema e mostrou que ao conhecer
uma raiz de uma equação cúbica, conseguimos encontrar as outras duas. Por exemplo, se x =
4. Sabemos que a soma das outras duas raízes deve ser 4, logo a parte real da equação é 2.
Bombelli teve a ideia de somar um número imaginário a esta parte real, e na outra raiz somar
o inverso relativo à adição deste número imaginário. Mais tarde, essa teoria vai ficar
conhecida como raiz conjugada.
René Descartes escreveu no seu livro Géométrie a seguinte frase: “Nem sempre as
raízes verdadeiras (positivas) ou falsas (negativas) de uma equação são reais. Às vezes elas
são imaginárias”. Com esta citação ficou definido que o número raiz quadrada de -1 seria
chamado de número imaginário e que poderia ser manipulado de acordo com as regras da
álgebra.
Abraham de Moivre foi um grande matemático e ficou conhecido pela fórmula de
Moivre, que relaciona os números complexos com a trigonometria. Provavelmente Moivre
descobriu esta relação em 1707.
Tudo na matemática possui uma simbologia, seja o sinal de divisão, seja uma integral,
então como ficariam definidos estes números imaginários? Foi Leonhard Euler que criou
vários símbolos, assim à raiz quadrada de -1 seria simbolizada por i, em 1777. Segundo Euler,
os números complexos também podem possuir uma parte real. Logo, o número complexo é do
tipo: z = a + bi, onde a e b são números reais e i² = -1, mas esta ideia só foi aceita quando
Gauss introduziu esta ideia.
Em 1797, Caspar Wessel trabalhou geometricamente os números complexos, fazendo
uma correspondência objetiva entre estes e os pontos do plano, mas somente foi publicado em
1806, por Jean Argand. Hoje, Argand recebe o mérito por esta representação. Em 1798 o
matemático Carl Friedrich Gauss demonstrou em sua tese de doutorado que toda equação
algébrica de grau n (n > 0) e coeficientes complexos, tem pelo menos uma raiz complexa.
Esse é o chamado Teorema Fundamental da Álgebra. Tal teorema resolveu a questão das
soluções de equações algébricas.
Em 1831, Gauss retomou a ideia Argand e pensou nos números a + b(raiz -1), como
coordenadas de um ponto em um plano cartesiano, tendo assim (a, b). Deu-se também uma
interpretação geométrica para a adição e multiplicação dos símbolos. Esta representação
geométrica, fez com que os matemáticos se sentissem muito mais à vontade quanto aos
números imaginários, pois estes agora podiam ser visualizados no sentido de que cada ponto
no plano corresponde a um número complexo e vice versa. E para finalizar, em 1832, Gauss
introduz a expressão número complexo.
5.3. Operacionalização da aula:
Retomando: Conjuntos numéricos
Iniciar a aula resolvendo algumas equações e classificando os resultados em seus
respectivos conjuntos.
1. Resolva as seguintes equações abaixo, classificando os resultados nos conjuntos
numéricos.
a) x2 – 25 = 0
b) 2x + 5 = 1
c) 2x + 1 = 4
d) x2 - 2= 0
e) x2 + 4 = 0
O conjunto dos números complexos
O surgimento dos números complexos levou a uma ampliação dos conjuntos numéricos
tendo sido criado, então, o conjunto dos números complexos.
₵ = 𝐙|𝐙 = 𝐚 + 𝐛𝐢, 𝐜𝐨𝐦 𝐚, 𝐛 ∈ ℝ 𝐞 𝐢𝟐 = −𝟏
Todo número complexo z pode ser escrito da maneira única na forma: z = a + bi em
que a, b ∈ ℝ, e i é a unidade imaginária.
Essa é a chamada forma algébrica do número complexo z. Observemos que um número
complexo escrito nessa forma tem duas partes:
Z = a + bi
Parte
real
Parte
imaginária
i é a unidade imaginária, tal que i2 = -1.
Exemplos:
a) z = 3 -2i é um número complexo com Re(z) = 3 e Im(z) = -2
b) z = 3 = 3 + 0i é um número complexo com Re(z) = 3 e Im(z) = 0
Nesse caso, z é também m número real, pois a parte imaginária de z é nula.
c) z = 4i = 0 + 4i é um número complexo com Re(z) = 0 e Im(z) = 4
Nesse caso, z é chamado imaginário puro, pois a parte real de z é nula.
Igualdade de número complexo
Dados dois números complexos z = a + bi e w = c + di, com a, b, c, d ∈ ℝ, definimos a
igualdade z = w quando Re(z) = Re(w) e Im(z) = Im(w), ou seja:
z = w ⇔ a + bi = c + di ⇔ a = c e b = d
Exemplo:
Os números complexos z = 8 + bi e w = a − 2i, com a, b ∈ ℝ, são iguais se, e somente se:

Re(z) = Re(w) ⇒ 8 = a

Im(z) = Im(w) ⇒ b = − 2
Operações com números complexos
Adição e subtração de números complexos:
Dados dois números complexos z = a + bi e w = c + di, com a, b, c, d ∈ ℝ, podemos
definir as operações de adição e subtração entre z e w da seguinte forma:
Adição: z + w = (a + bi) + (c + di) = a + bi + c + di = (a + c) + (b + d)i
Subtração: z - w = (a + bi) - (c + di) = a + bi - c - di = (a - c) + (b - d)i
Exemplos:
Sejam os números complexos z1 = 1 + 3i, z2 = i e z3 = -7. Vamos calcular:
a) z1 + z2 + z3 = (1 + 3i) + (0 + i) + (-7 + 0i) = 1 + 3i + 0 + i -7 + 0i
= (1 + 0 -7) + (3 + 1 + 0)i = -6 + 4i
b) z2 – (z1 + z3) = i – (1 + 3i -7) = i – (1 -7 + 3i) = i – (-6 + 3i) = i + 6 – 3i = 6 – 2i
Multiplicação de números complexos:
Dados dois números complexos z = a + bi e w = c + bi, com a, b, c, d ∈ ℝ, podemos
efetuar a multiplicação entre z e w aplicando a propriedade distributiva:
z . w = (a + bi)(c + di) = ac + adi +bci + bdi2
Exemplo:
Dados os números complexos z1 = 1 + i, z2 = 4 – 2i e z3 = 5, vamos calcular:
a) z1 . z2 = (1 + i).(4 – 2i) = 4 – 2i + 4i - 2i2 = 4 + 2i – 2.(-1) = 4 + 2i + 2 = 6 + 2i
b) (z2)2 = (4 – 2i)2 = (4 – 2i).(4 – 2i) = 16 – 8i – 8i + 4i2 = 16 – 16i + 4.(-1)
= 16 – 16i – 4 = 12 – 16i
c) 2. (z1.z2.z3) = 2.[(1 + i)(4 – 2i)(5)] = 2.[(1 + i)(20 – 10i)] = 2.[20 – 10i + 20i – 10i2]
= 2. [20 + 10i +10] = 2. [30 + 10i] = 60 + 20i
O conjugado de um número complexo:
Dado um número complexo z = a + bi, com a, b ∈ ℝ, chamamos de conjugado de z,
cuja notação é z, o número complexo z = a – bi.
Para obter z, basta trocar o sinal da parte imaginária de z.
Exemplo:
Os conjugados dos números complexos z1 = 1 + i, z2 = -3 – 5i, z3 = 3 e z4 = -i são:
z1 = 1- i, z2 = -3 + 5i, z3 = 3 e z4 = i
Divisão de número complexo:
Dados dois números complexos z e w, com w, com w ≠ 0, podemos efetuar a divisão
entre z e w por meio de um processo semelhante à racionalização de denominadores. Para
z
obter o quociente w , multiplicamos numerador e denominador pelo conjugado do
denominador (w).
Assim:
𝐳
𝐰
=
𝐳.𝐰
𝐰. 𝐰
Exemplo:
1 −2+i
Calcular os quocientes: ,
i

1
i
=
1.(−i)
i.(−i)
=
−i
−i 2
3−2i
=
e
−i
−(−1)
(3−2i)2
−2+i
=
−i
1
.
= −i
−2+i

3−2i
=
(3−2i)2

22
5
3−2i .(3+2i)
=
−2+i
−
−2+i .(3+2i)
+
19
5
9−12i+4i 2
−2+i
=
=
−6−4𝑖+3𝑖+2𝑖 2
9+6𝑖−6𝑖−4𝑖 2
5−12i
−2+i
=
=
−8−𝑖
13
5−12i . −2−i
=−
=
−2+i . −2−i
8
13
−
1
13
i
−10−5i+24i+12i 2
4+2i−2i−i 2
=
−22+19i
5
=
i
As potências de i
i0 = 1
i4 = i2 . i2 = −1 . −1 = 1
i1 =i
i5 = i2 . i2 . i = i
i2 =-1
i6 = i2 . i2 . i2 = −1
i3 = i2 . i = −1. i = −i
i7 = i2 . i2 . i2 . i = −i
As potências de i se repetem em grupos de quatro valores, seguindo o padrão das
potências i0 , i1 , i2 e i3 . Então, para calcular a potência in , com n ∈ ℕ, efetuamos a divisão de
n por 4 e consideramos o resto dessa divisão como o novo expoente de i.
Exemplos:
Simplificar:
3i 44 +12i 33
−3i 50
→
3.1+12.i
−3.(−1)
=
3+12i
3
3
12i
3
3
= +
= 1 + 4i
i44 = i0 = 1
i33 = i1 = i
i50 = i2 = −1
Representação geométrica de um número complexo
Da mesma forma que a cada número real pode-se associar um único ponto da reta real, a
cada elemento a + bi (com a, b ∈ ℝ) do conjunto dos números complexos corresponde um
único ponto P(a, b) do plano cartesiano e vice-versa. A parte real de z é representada no eixo
das abscissas, que é chamado de eixo real, e a parte imaginária, no eixo das ordenadas, que é
o eixo imaginário.
O plano cartesiano assim definido passa a ser chamado de plano de Argand-Gauss ou
plano complexo. O ponto P(a, b) é a imagem de z nesse plano ou o afixo do número
complexo z = a + bi (com a, b ∈ ℝ).
Exemplo:
Vamos representar no plano complexo as imagens dos números complexos: z1 = 3 – i, z2 = 4i
e z3 = -1.
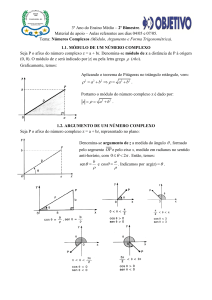
Módulo de um número complexo
O módulo de z = a + bi, indicado por |z| ou 𝛒, é o módulo do vetor 𝑂𝑃 que o representa
(comprimento do vetor), ou seja, é a distância da origem O(0,0) ao ponto P(a,b).
a−0
Assim, no triângulo OAP, temos: |z| = dO,P =
|z| = 𝛒 =
2
+ (b − 0)² =
a² + b²
𝐚² + 𝐛²
Argumento de um número complexo
A direção do vetor 𝑂𝑃 é dada pelo ângulo θ (com 0 ≤ θ < 2𝜋), formado pelo vetor e
pelo semieixo real positivo, considerado no sentido anti-horário. Para um complexo não nulo
z (z = a + bi, com a, b ∈ ℝ), o ângulo θ é chamado de argumento de z, indicado por arg(z).
Também temos que:
𝐛
𝐚
θ é o ângulo tal que sen θ = 𝛒 e cos θ = 𝛒, com 𝛒 = 𝐳 𝐞 𝟎 ≤ 𝛉 < 𝟐𝛑
Exemplo:
Representar geometricamente o número complexo z = 2 + 2i e obter o módulo e o argumento
de z.
O módulo de z é dado por: ρ = dO,P 2² + 2² = 8 = 2 2
Para obter o argumento de z, vamos considerar o triângulo retângulo OAP.
sen θ =
cos θ =
AP
OP
OA
OP
=
Im (z)
=
Re (z)
ρ
ρ
=
=
2
2 2
2
2 2
=
1
=
1
Como 0 ≤ θ < 2𝜋, temos θ =
2
2
π
4
.
2
.
2
2
2
=
=
ou 45°.
2
2
2
2
A forma trigonométrica de um número complexo
Vamos ver agora como expressar o número complexo z = a + bi, não nulo e com a, b
∈ ℝ, por meio de suas coordenadas polares, obtendo a chamada forma trigonométrica ou
forma polar de z.
Já sabemos que:
ρ=
b
a² + b²
a
sen θ = ρ → b = ρ. senθ
cos θ = ρ → a = ρ. cosθ
Substituindo esses valores na forma algébrica de z, temos:
z = a + bi = ρ . cos θ + ρ . sen θ . i = ρ . cos θ + ρ . i. sen θ
z = 𝛒(𝐜𝐨𝐬 𝛉 + 𝐢 . 𝐬𝐞𝐧𝛉)
Exemplo:
Escrever z = -1 + 1 na forma trigonométrica e representa-lo geometricamente.
ρ=
a² + b² →
sen θ =
θ=
b
ρ
=
1
2
ρ=
(−1)² + 1² = 2
2
=
cos θ =
2
a
ρ
=
−1
2
=−
2
2
3𝜋
4
Logo: z = ρ(cos θ + i . senθ)
z = 2 . (cos
3𝜋
4
+ i . sen
3𝜋
4
)
O número complexo z pode ser representado por um vetor de módulo 2 e direção θ =
ou 135°.
3𝜋
4
Operação na forma trigonométrica
Multiplicação e divisão: considere os números complexos z1 e z2 de módulo 𝜌1 e 𝜌2 e
argumento 𝜃1 e θ2 , respectivamente não nulos, na forma trigonométrica:
z1 = 𝜌1 (cos 𝜃1 + i . sen𝜃1 ) e

z2 = 𝜌2 (cos 𝜃2 + i . sen𝜃2 )
Vamos obter o produto z1z2:
z1z2 = [ρ1 (cos θ1 + i . senθ1 )] . [ρ2 (cos θ2 + i . senθ2 )]
= ρ1 ρ2 (cos θ1 + i . senθ1 ) . (cos θ2 + i . senθ2 )
= ρ1 ρ2 (cos θ1 . cos θ2 + i . cos θ1 . senθ2 + i. sen θ1 . cosθ2 + i². sen θ1 . senθ2 )
= ρ1 ρ2 [(cos θ1 . cos θ2 − sen θ1 . senθ2 ) + i. ( cos θ1 . senθ2 + sen θ1 . cosθ2 )]
Assim: z1z2 = 𝛒𝟏 𝛒𝟐 [𝐜𝐨𝐬(𝛉𝟏 + 𝛉𝟐 ) + 𝐢 . 𝐬𝐞𝐧(𝛉𝟏 + 𝛉𝟐 )]

z1
z2
=
=
=
Vamos obter o quociente
ρ 1 (cos θ 1 +i .sen θ 1 )
ρ 2 (cos θ 2 +i .sen θ 2 )
=
z1
z2
multiplicando-o por
z2
z2
:
ρ 1 (cos θ 1 +i .sen θ 1 )(cos θ 2 −i .sen θ 2 )
ρ 2 (cos θ 2 +sen θ 2 )(cos θ 2 −i .sen θ 2 )
ρ 1 cos θ 1 . cos θ 2 −i .cos θ 1 . sen θ 2 + i .sen θ 1 .cos θ 2 −i 2 . sen θ 1 . sen θ 2
.
ρ2
cos ² θ 2 +sen ² θ 2
ρ 1 (cos θ 1 . cos θ 2 +sen θ 2 )+i .( sen θ 1 . cos θ 2 −. sen θ 2 . cos θ 1 )
.
ρ2
1
𝐳
𝛒
Assim: 𝐳𝟏 = 𝛒 𝟏 [𝐜𝐨𝐬 𝛉𝟏 − 𝛉𝟐 + 𝐢 . 𝐬𝐞𝐧(𝛉𝟏 − 𝛉𝟐 )]
𝟐
𝟐
Exemplo:
π
π
π
π
Dados os números complexos z1 = 3 . cos 2 + i . sen 2 e z2 = 4 . cos 4 + i . sen 4 , calcular:
a)
z1
z2
→
=
ρ1
ρ2
3
4
[cos θ1 − θ2 + i . sen(θ1 − θ2 )] =
𝜋
3
4
[cos
𝜋
𝜋
𝜋
𝜋
− 4 + i . sen( 2 − 4 )]
2
𝜋
(cos 4 + i . sen 4 )
𝜋
𝜋
𝜋
𝜋
𝜋
𝜋
b) z1z1 → 3² . (cos 2 + i . sen 2 ) . (cos 2 + i . sen 2 ) = 9 . [(cos 2 )² − (i . sen 2 )²]
𝜋
𝜋
𝜋
𝜋
= 9 . (cos² 2 − i² . sen² 2 ) = 9 (cos² 2 +. sen² 2 ) = 9 . 1 = 9
Potenciação: 1ª Formula de De Moivre
Considere o número complexo z, não nulo, na forma trigonométrica. Vamos obter
𝑧 𝑛 = [𝜌(𝑐𝑜𝑠 𝜃 + 𝑖 . 𝑠𝑒𝑛𝜃)]n , com n ∈ ℕ e n > 1, recorrendo à multiplicação de complexos na
forma trigonométrica vista anteriormente.
Zn = z.z. …. z.z = 𝜌(𝑐𝑜𝑠 𝜃 + 𝑖 . 𝑠𝑒𝑛𝜃) . 𝜌(𝑐𝑜𝑠 𝜃 + 𝑖 . 𝑠𝑒𝑛𝜃) . … . 𝜌(𝑐𝑜𝑠 𝜃 + 𝑖 . 𝑠𝑒𝑛𝜃) =
= 𝜌. 𝜌. … . 𝜌. 𝜌. [𝑐𝑜𝑠 𝜃 + 𝜃 + ⋯ + 𝜃 + 𝜃 + 𝑖. 𝑠𝑒𝑛(𝜃 + 𝜃 + ⋯ + 𝜃 + 𝜃]
Ou seja: 𝐳 𝐧 = 𝛒𝐧 . (𝐜𝐨𝐬 𝐧𝛉 + 𝐢. 𝐬𝐞𝐧 𝐧𝛉)
Exemplo:
π
π
Dado z = 2. (cos 3 + i. sen 3 ), vamos calcular z7.
π
π
7π
3
3
3
z 7 = 27 . [cos(7. ) + i. sen(7. )] = 128. (cos
+ i. sen
5.4. Conclusão da aula (atividades e sugestão de atividade).
Lista de Exercícios:
1. Calcule as seguintes somas:
a) (2 + 5i) + (3 + 4i)
b) i + (2 - 5i)
2. Calcule as diferenças:
a) (2 + 5i) - (3 + 4i)
b) (1 + i) - (1 - i)
3. Calcule os seguintes produtos:
a) (2 + 3i) (3 - 2i)
b) (1 + 3i) (1 + i)
4. Escreva os conjugados dos seguintes números complexos:
a) 3 + 4i
b) 1 - i
c) –3 + i
d) –2 –5i
6. Efetue as seguintes divisões de números complexos:
7π
3
)
a) (-10 + 15i) / (2 – i)
b) (1 + 3i) / (1 + i)
6. Avaliação:
A avaliação dar-se-á observando a participação e o interesse do discente em sala de aula
e na resolução do exercício proposto, considerando as respostas dadas aos questionamentos
sugeridos permitindo se houve entendimento sobre os conteúdos, conforme documento em
apêndice.
6.1. Instrumentos de avaliação
O processo avaliativo será operacionalizado durante o decorrer das aulas e ao concluir
os conteúdos será aplicada uma avaliação
7. Bibliografia
DANTE, Luiz Roberto. Matemática: Contexto & Aplicações. 2. ed. - Ática. São Paulo,
2013.
LEONARDO, Fabio Martins de. Conexões com a Matemática. Organização editora
moderna 2. ed. São Paulo: Moderna 2013.
PAIVA, Manoel. Matemática: Paiva. 2. ed.- São Paulo: Moderna, 2013.
APÊNDICE
Escola de Educação Básica Professora Maria Solange Lopes de Borba
Professora: Suzana Scandolara Selau
DISCIPLINA: Matemática
Data: 03/11/2014
Aluno (a):............................................................................................Série: 3º ano
PROVA
1) Classifique as afirmações abaixo como verdadeiras ou falsas. Justifique sua resposta para
as falsas.
( ) O número − 5 não é complexo ,pois não pode ser escrito na forma algébrica z = a + bi.
( ) Todo número complexo é real, mas nem todo número real é complexo.
( ) Com o aparecimento dos números complexos, tornou-se possível resolver equações do 2°
grau nas quais o discriminante (∆) é negativo.
( ) A parte imaginária de um número complexo pode ser um número irracional.
( ) A parte real de um número complexo não pode ser um número racional.
2) Identifique e escreva a parte real e a parte imaginária de z em cada caso.
a) z = 3 − i. 5
b) 𝑧 =
d) z = 9i
1+2i
e) z = 4
3
c) z = - i
3) Some a(s) alternativas que você considera correta(s):
01. A multiplicação de z. z do número complexo z = - 3 – 2i é igual a 13.
02. A parte real de z é representada no eixo das ordenadas, que é chamado de eixo real, e a
parte imaginária, no eixo das abscissas, que é o eixo imaginário.
b
a
04. θ é o ângulo tal que sen θ = ρ e cos θ = ρ com ρ = z e 0 ≤ θ ≤ π.
08. Efetuando o seguinte equação 2i8 + (1 + 4i)2 é igual a -13 + 8i.
Soma:
4) Escreva z = 2i na forma trigonométrica e representá-lo geometricamente.