Simulação do Campo Elétrico e Equipotenciais

CAPÍTULO
4
Simulação do Campo Elétrico e Equipotenciais
Prof. Cláudio Graça, Dep. Fı́sica UFSM
4.1
Introdução
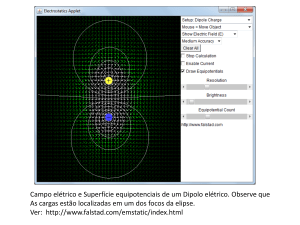
O campo elétrico, pode ser representado, graficamente, de duas maneiras, ou através das
linhas de campo elétrico, ou através das superfı́cies equipotenciais. Neste experimento vamos simular o campo elétrico em pontos do mapa de campo, utilizando um aplicativo livre distribuı́do pela
Sociedade Brasileira de Fı́sica no site:
http : //pion.sbfisica.org.br/pdc/index.php/por/multimidia/simulacoes/eletromagnetismo/
simulador de campo eletrico.
O campo será simulado para condutores como os apresentados no roteiro da aula anterior,
simulando as superfı́cies metálicas com cargas elétricas pontuais. O resultado serão figuras como as
abaixo, nas quais a simulação permite obter o campo elétrico e as linhas equipotenciais.
Figura 4.1: Traços das superfı́cies equipotenciais para diferentes distribuições de carga; (a) carga
pontual; (b) dipolo; (c) monopolo de duas cargas positivas.
4.1.1
Objetivos
• Simular matemáticamente o campo elétrico e suas linhas equipotenciais;
• medir o potencial elétrico sobre linhas ou superfı́cies equipotenciais, utilizando o aplicativo;
• observar com as simuações e comparar com os resultados obtidos com as previsões teóricas.
17
C.O. GRAÇA
4.1.2
Experimentos de Fı́sica: Eletricidade e Magnetismo
Experimentos
Faça a simulação das distribuições de carga elétrica abaixo, utilizando cargas pontuais fornecidas pelo simulador na escala desejada:
1. Carga pontual positiva.
2. Carga pontual negativa.
3. Duas cargas positivas distanciadas entre si por uma distância de 6 unidades do papel.
4. Um dipolo (uma carga positiva e uma negativa com a mesma disposição do item anterior.
5. Um quadrupolo, constituı́do de duas cargas negativas colocadas na origem 2q e duas distanciadas de 5 unidades em sentidos opostos.
6. Quatro cargas positivas colocadas nos vértices de um quadrado de lado 5 unidades.
7. Um capacitor de placas planas (duas linhas de carga paralelas uma positiva e outra negativa)
paralelas.
8. Um capacitor esférico, representado por dois cı́rculos de cargas opostas, concêntricos.
9. Um eletroscópio de folhas, simulado por cargas pontuais.
10. Um corpo condutor com uma ponta, com o mesmo aspecto da Figura 3.10 do livro.
4.1.3
Fundamentos das Medidas
Medida de Potencial As medidas de potencial serão realizadas com o aplicativo e seu cursor, o
sistema de referência será de papel milı́metrado com escala adequada...
Relação entre Campo Elétrico e as Superfı́cies Equipotenciais
A Figura abaixo nos mostra a relação entre as linhas de campo e as equipotenciais. A força
Figura 4.2: Relação entre as linhas equipotenciais e os vetores campo elétrico
c Cláudio Graça
°
18
C.O. GRAÇA
Experimentos de Fı́sica: Eletricidade e Magnetismo
sobre os elétrons do meio ohmico é dada por:
~
F~ = q F~ = −eE,
cuja direção será oposta à do campo elétrico. Quando uma carga q, qualquer, sofrer um deslocamento
~ sofrerá uma variação de energia potencial eletrostática:
∆~s no campo elétrico E
~ · ∆~s.
q∆V = −F~ · ∆~s = −q E
Portanto a relação entre o potencial elétrico e o campo elétrico poderá ser obtida, através da relação:
~ · ∆~s,
∆V = −E
ou de forma escalar,
∆V = −E∆scosθ.
No caso do deslocamento na direção definida pelo campo elétrico, a relação será:
E=−
∆V
,
∆s
também definida pelo gradiente do potencial:
~ = −gradV = −∇V.
E
4.2
Relatório
1. Descreva os experimentos em detalhe e sua construção no simulador.
2. Apresente as medidas do potencial de forma gráfica, construindo as linhas equipotenciais utilizando o gráfico do simulador
3. Determine o campo elétrico a partir das medidas de potencial entre duas superfı́cies equipotenciais, localizando o vetor campo na figura em três diferentes pontos.
4. Apresente as linhas equipotenciais, torno da ponta no experimento do corpo de ponta e discuta
as suas caracterı́sticas, no sentido de entender o efeito de pontas.
5. Descreva as caracterı́sticas do campo em cada uma das distribuições de carga elétrica.
Bibliografia Fundamentos de Fı́sica, v. 3, Halliday & Resnick; Fı́sica, v. 3, Paul Tipler.
c Cláudio Graça
°
19