campo elétrico e contornos equipotenciais - Feg

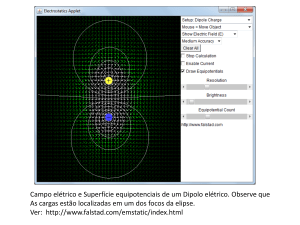
CAMPO ELÉTRICO E CONTORNOS EQUIPOTENCIAIS
UNESP - Faculdade de Engenharia - Campus de Guaratinguetá
1
0.1. Introdução
Nesta prática vamos obter o traçado de contorno equipotenciais na vizinhança de eletrodos em
uma cuba eletrolı́tica e determinar o campo elétrico em alguns pontos desta região.
0.2. Fundamentos
0.2.1. Superfı́cies e contornos equipotenciais.
Em um corpo condutor eletricamente carregado e em equilı́brio eletrostático o potencial
elétrico é igual em todos os pontos, tanto no interior quanto na sua superfı́cie. Na região externa
o módulo do potencial varia, diminuindo a medida que nos afastamos do corpo. A superfı́cie do
corpo constitui a primeira superfı́cie equipotencial
e sua geometria, é claro, é a do próprio corpo. A
medida que nos afastamos sua forma se altera até
atingir uma geometria esférica em pontos muito
distantes. Neste limite o corpo de dimensões fini- Fig. 1 - Superfı́cies equipotenciais e contornos de
equipotenciais de um disco eletricamente carregado.
tas passa a ser considerado uma carga pontual.
Aqui nos interessa a região próxima aos corpos carregados, como a mostrada na Fig.1. A figura
ilustra as superfı́cies equipotenciais de um disco carregado e os contornos equipotenciais formados
pela intersecção destas superfı́cies com um plano. Ilustração semelhante é mostrada na Fig.2 para
um anel ou um cilindro vazado finito e carregado. Já na Fig.3 temos o gráfico do potencial de dois
anéis carregados com cargas de sinais opostos e mesma magnitude. A figura mostra o contornos
equipotenciais e sua projeção no plano. Contornos semelhantes podem ser obtidos em uma cuba
eletrolı́tica, onde em uma solução eletrolı́tica colocamos dois eletrodos na forma de anéis e , com
um circuito de alimentação, fazermos uma corrente fluir entre os eletrodos através da solução.
⃗ e o potencial elétrico ϕ estão relacionados pela
0.2.2. Campo elétrico. O campo elétrico E
equação:
(0.1)
⃗
E(x,
y, z) = −∇ϕ(x, y, z)
Experimentalmente, com um voltı́metro, mede-se a diferença de potencial (ddp) V (x, y, z). Na
medição conectamos o terminal COM (ou o polo −) do instrumento em um ponto (x0 , y0 , z0 ) do
1
Roteiro para laboratório de Eletricidade, Magnetismo e Ótica elaborado por Milton E. Kayama, docente do
Departamento de Fı́sica e Quı́mica. abr-2010
1
2
circuito onde o potencial é ϕ(x0 , y0 , z0 ) = ϕ0 . O segundo terminal é conectado ao ponto (x, y, z) do
mesmo circuito onde o potencial é ϕ(x, y, z). Portanto a ddp V medida é:
(0.2)
V (x, y, z) = ϕ(x, y, z) − ϕ0
Substituindo 0.2 em 0.1 e como ∇ϕ0 = 0 teremos:
(0.3)
⃗
E(x,
y, z) = −∇V (x, y, z)
No caso unidimensional onde V depende apenas da coordenada espacial x teremos:
(0.4)
d
∆V
⃗
E(x)
= − V (x) ≈ −
dx
∆x
onde ∆x = x2 − x1 e ∆V = V (x2 ) − V (x1 ), supondo ∆x suficientemente pequeno.
15
( volt )
10
0 V
+1 V
5
- 1 V
0
UN
P
ES
- M
AM
AY
.K
.E
A
-5
-10
-15
-5
+1 V
0
x
0 V
(
m
c
0
)
-5
10
-10
10
5
- 1 V
5
cm
y (
)
Fig. 2 - Equipotenciais em um anel carregado. Fig. 3 - Potencial elétrico em um arranjo de
dois anéis carregados.
A derivada pode ser também calculada usando o método das diferenças finita. Para isso vamos
supor um conjunto de N valores de V medidos ao longo do eixo x e arranjados na forma:
Segundo este método, supondo intervalos espaciais xj+1 − xj pequenos, o campo elétrico Ej no
ponto xj é dado por:
(0.5)
Ej = −
Vj+1 − Vj−1
2∆x
onde
(0.6)
∆x = xj+1 − xj = xj − xj−1
0.3. PRÁTICA
3
Esta fórmula se aplica em pontos intermediários. Para o primeiro e último ponto usamos respectivamente:
E1 = −
(0.7)
EN = −
(0.8)
V2 − V1
∆x
VN − VN −1
∆x
que dependem apenas do ponto vizinho imediato.
Fig. 4 - Cuba eletrolı́tica.
Fig. 5 - Circuito elétrico da experiência
da cuba eletrolı́tica.
0.3. Prática
Para determinaremos contornos equipotenciais e o campo elétrico vamos usar uma cuba eletrolı́tica.
Na cuba (Fig.4) teremos uma solução aquosa de um sal (solução condutora) onde colocamos os
eletrodos metálicos. Conectando os eletrodos a uma fonte de alimentação externa e teremos uma
corrente elétrica fluindo pela solução. Nesta condição os contornos equipotencias na solução são
idênticos a desses eletrodos em vácuo, carregados com a mesma carga mas de sinais opostos.
Para a montagem da experiência, siga as etapas:
1 - em duas folhas de papel milimetrado, trace duas retas ortogonais (eixo x e eixo y). Cruzeos próximo ao meio da folha e defina eixo x como o eixo maior;
2 - use uma das folhas para definir um sistema de coordenadas na cuba. Para isso coloque a
cuba sobre uma dessas folhas com seus lados paralelos aos eixos. A outra folha será usada
para marcar os pontos de contornos equipotenciais, como explicado mais adiante;
3 - coloque os eletrodos no interior da cuba posicionando seu centro sobre eixo x e simétricos
em relação ao eixo y;
4 - despeje o eletrólito ( solução aquosa de sulfato de cobre ) na cuba até uma altura aproximada de 5mm.
Atenção: a solução de sulfato de cobre é tóxica.
Não ingerir. Ao entrar em contato com a pele lave
imediatamente o local com água corrente.
5 - ligue os eletrodos ao circuito de elimentação mostrado no esquema da Fig.5. Neste esquema
Rs é a resistência elétrica do do arranjo eletrodo-eletrólito-eletrodo.
4
6 - coloque no zero os botões de controle da fonte girando-os para a esquerda. Depois ligue
a fonte e coloque no valor ditado pelo professor. Procure deixar o circuito sem corrente
caso não esteja fazendo as medições.
0.3.1. Contornos Equipotenciais. Para determinarmos os contornos equipotenciais vamos
usar um microamperı́metro que fornece valores positivos e negativos da corrente. Este instrumento
indicará uma corrente nula quando seus dois terminais estiverem sobre uma mesma equipotencial.
Para a medição, supondo a cuba ligada como instruido no item anterior, proceda da seguinte forma:
1 - fixe o suporte de terminal na borda da cuba deixando a extremidade do condutor no
interior da solução;
2 - conecte este terminal a um dos terminais do microamperı́metro. Esta é a ponta fixa;
3 - no outro terminal do microamperı́metro conecte um fio que tenha um ponta de prova fina
e longa. Esta será a ponta móvel
Atenção: nunca submergir a ponta móvel na solução em um ponto distante
daquele onde se encontra a ponta fixa. A ddp entre os dois pontos pode ser elevada
e a alta corrente decorrente irá danificar o microamperı́metro.
4 - coloque a ponta móvel na solução, encostada à ponta fixa. Mova-a e localize os pontos
onde a corrente é nula. Anote o ponto na segunda folha milimetrada. Continue movendo
e localizando outros pontos da equipotencial até poder vizualizar todo seu contorno;
5 - mude a posição da ponta fixa na solução e repita o procedimento para traçar o contorno
equipotencial que passa por este novo ponto.
6 - posicione a ponta fixa em diversos locais da cuba de modo que no final seja possivel
visualizar diversas equipotenciais.
0.3.2. Campo elétrico. Vamos determinar o campo elétrico entre os eletrodos, ao longo da
reta que une os centros dos eletrodos. Para isso vamos realizar medições de V com um voltı́metro
que forneçe valores positivos e negativos da ddp. Primeiro, ligue a cuba conforme instruções dadas
anteriormente e proceda da seguinte forma:
1 - conecte, com um fio, o terminal COM (ou o polo −) do voltı́metro em um ponto qualquer
do circuito;
2 - no outro terminal do voltı́metro conecte um fio que tenha uma ponta de prova fina e longa.
Será a ponta móvel;
3 - com a ponta móvel no interior da solução realize as medições de V ao longo da reta que
une o centro dos eletrodos. Use intervalos regulares de 5 mm.
0.4. Relatório
Usando os pontos identificados como sendo de uma mesma equipotencial, determinados com
o microamperı́metro, interpole manualmente os pontos e obtenha o esboço dos contornos equipotenciais. Usando estes contornos faça o esboço de algumas linhas de campo elétrico. Com as
ddp’s medidas com o voltı́metro, determine o campo elétrico ao longo da reta que une o centro dos
eletrodos.