F10 - JoaoNarciso.com

Escola Secundária Alfredo Reis Silveira
Ano lectivo 2008/2009
MATEMÁTICA 11º PG
Ficha de Trabalho 10 – Funções Racionais
1. O que é uma função racional?
 Uma função racional é uma função definida por: f x  
n( x )
, onde n(x) e d ( x)  0 são polinómios.
d ( x)
Exemplos:
f x  
1
x2
1
x3  x
x2
, g x  
, h x   2
, ix    3
, l x  
são funções racionais.
x
x
x 1
x 1
x 4
2. Como se determina o domínio de uma função racional?
 O domínio de uma função racional é dado pelo conjunto dos números reais que não anulam o
denominador. Assim, para f x  
n( x )
, temos que D f  x  R : d ( x)  0.
d ( x)
Exemplos:
x2
, D f  x  R : x  0  R \ 0
x
x3  x
, Dh  x  R : x 2  4  0  R \  2, 2
h x   2
x 4
f x  

x2
1
, Dg  x  R : x  1  0  R \ 
x 1
1
3
ix    3
, Dg  x  R : x  1  0  R \  1
x 1
g x  



3. Quais as características de um gráfico de uma função racional ”tipo”?
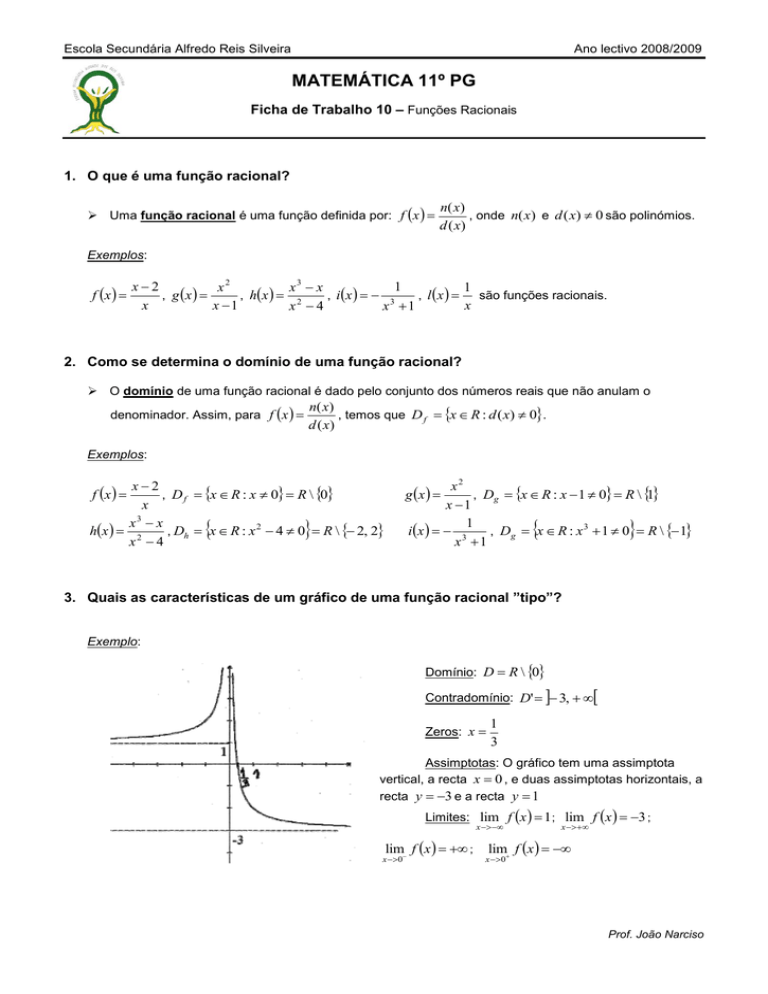
Exemplo:
Domínio: D  R \ 0
Contradomínio: D'   3,  
Zeros: x 
1
3
Assimptotas: O gráfico tem uma assimptota
vertical, a recta x  0 , e duas assimptotas horizontais, a
recta y  3 e a recta y  1
Limites: lim f x   1 ; lim f x   3 ;
x 
lim f x    ;
x  0 
x 
lim f x   
x  0 
Prof. João Narciso
4. O que é uma assimptota de um gráfico?
 Assimptota vertical: A recta de equação x  a é uma assimptota vertical do gráfico se e só se
lim f x    (ou  )
x a 
ou
lim f x    (ou  ) .
x a 
 Assimptota horizontal: A recta de equação y  b é uma assimptota horizontal do gráfico se e só se
lim f x   b
x 
ou
lim f x   b .
x 
5. Como se determinam as assimptotas de um gráfico?
 Assimptota vertical:
Seja f x  
n( x )
uma função racional. Se a é um número tal que d (a)  0 e n(a)  0 , então a recta
d ( x)
x  a é assimptota vertical do gráfico.
Exemplo:
x2
, D f  x  R : x  0  R \ 0 . Ora temos que 0 é zero do denominador e não é zero do
x
denominador, logo a recta x  0 é uma assimptota vertical do gráfico.
f x  
 Assimptota horizontal:
Seja f x  
an x n  an1 x n1  ...  a1 x  a0
uma função racional.
bm x m  bm1 x m1  ...  b1 x  b0
o
Se n  m , a recta de equação y  0 é assimptota horizontal do gráfico de f .
o
Se n  m , a recta de equação y 
o
Se n  m , o gráfico da função f não tem assimptotas horizontais.
an
é assimptota horizontal do gráfico de f .
bm
Nota: Numa função racional existem, no máximo, duas assimptotas horizontais.
Exemplos:



x2
1
, como o grau do numerador é igual ao grau do denominador então a recta y 
é
2x
2
assimptota horizontal de f .
f x  
x2
, como o grau do numerador é maior do que o grau do denominadordor então a recta
x2  4
y  0 é assimptota horizontal de f .
f x  
f x  
x3
, como o grau do numerador é menor do que o grau do denominador então f não tem
x2 1
assimptotas horizontais.
Prof. João Narciso