Capítulo 10 Excitação Senoidal e Fasores - DECOM

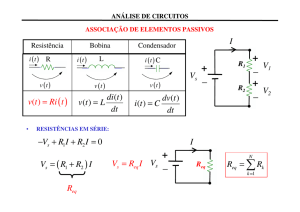
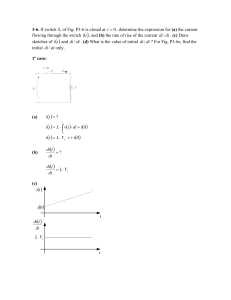
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Capítulo 10
Excitação Senoidal e Fasores
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
10.1 Propriedades das Senóides:
Onda senoidal:
Vm
()
( )
v t = Vm sen ω t
π/ω
Amplitude = Vm
-Vm
Frequência angular = ω [rad/s]
Senóide é uma função periódica:
(
) ()
v t +T = v t
Período: T = 2π/ω
Frequência: f = 1/T = ω/2π
Expressão geral: v t = Vm sen ω t + φ
()
onde φ é o ângulo de fase.
(
)
2π/ω
t
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Curva de uma senóide defasada de φ radianos:
()
(
v t = Vm sen ω t + φ
)
()
( )
v t = Vm sen ω t
φ/ω
π/ω
2π/ω
Note que:
!
π$
cos #ω t − & = sen ω t
2%
"
( )
!
π$
sen #ω t + & = cos ω t
2%
"
( )
t
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Determinação de quanto uma senóide antecede ou segue outra de
mesma frequência.
(
)
v1 = 4cos ω t + 30°
(
)
v2 = −2sen ω t +18°
(
)
v2 = 2sen ω t +18° +180°
(
)
v2 = 2cos ω t +18° +180° − 90°
(
)
v2 = 2cos ω t +108°
Portanto, v1 antecede v2 de 30º - 108º = -78º, ou v1 está defasada em relação a v2
de 78º.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Soma de uma senóide com uma cossenóide de mesma frequência:
!
$
A
B
Acos ω t + Bsen ω t = A + B #
cos ω t +
sen ω t &
#" A2 + B 2
%&
A2 + B 2
( )
( )
2
2
( )
()
cos θ
B
( )
()
sen θ
A2 + B 2
θ
A
Acos ω t + Bsen ω t = A2 + B 2 !"cos ω t cos θ + sen ω t sen θ #$
( )
( )
( ) ()
( ) ()
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Acos ω t + Bsen ω t = A2 + B 2 !"cos ω t cos θ + sen ω t sen θ #$
( )
( )
( ) ()
(
( ) ()
cos ω t − θ
Então,
Acos ω t + Bsen ω t = A2 + B 2 "#cos ω t − θ $%
( )
( )
(
" B%
θ = tan $ '
# A&
−1
Obs.:
)
cos(a)cos(b) + sen(a)sen(b) = cos(a - b)
cos(a)cos(b) - sen(a)sen(b) = cos(a + b)
)
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo:
( )
2
−5 +122 "#cos 3t − θ $%
( ) ( )
−5cos 3t +12sen 3t =
(
)
" 12 %
θ = tan $ ' = 112,6°
# −5 &
−1
( )
( )
(
)
−5cos 3t +12sen 3t = 13cos 3t −112,6°
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
10.2 Exemplo de um Circuito RL
Encontrar if .
R
vg = Vm cos(ωt)
+
-
i
L
L
di
+ Ri = Vm cos ω t
dt
( )
Por tentativa, temos: i f = Acos ω t + Bsen ω t
( )
L
( )
d!
Acos ω t + Bsen ω t #$ + R !" Acos ω t + Bsen ω t #$ = Vm cos ω t
"
dt
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
−Lω Asen ω t + Lω B cos ω t + RAcos ω t + RBsen ω t = Vm cos ω t
Então:
Lω B + RA = Vm
−Lω A + RB = 0
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Assim,
A=
B=
Portanto,
if =
mas
RVm
2
2 2
R +ω L
RVm
R 2 + ω 2 L2
ω LVm
R 2 + ω 2 L2
( )
cos ω t +
ω LVm
2
2 2
R +ω L
( )
sen ω t
Acos ω t + Bsen ω t = A2 + B 2 "#cos ω t − θ $%
( )
( )
(
" B%
θ = tan $ '
# A&
−1
Portanto,
if =
(
"
%+
−1 ω L
cos *ω t − tan $
'2
2 2
R
#
&,
)
R +ω L
Vm
)
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Então, podemos escrever a corrente forçada como:
i f = I m cos !"ω t + φ #$
onde
Im =
Vm
R 2 + ω 2 L2
"ω L %
φ = − tan $
'
R
#
&
−1
Resposta natural:
" R %
in = A1 exp $ − t '
# L &
A corrente se estabiliza em seu valor de regime permanente c.a. dado pela
corrente forçada.
Método muito trabalhoso para a obtenção das equações de corrente!
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
10.3 Método Alternativo utilizando Números Complexos
Para a análise de circuitos com excitação senoidal.
Propriedades dos números complexos:
Representação na forma retangular de um número complexo:
A = a + jb
onde j = −1 , a = parte real de A e b = parte imaginária de A.
Representação na forma polar:
A = A e jα = A ∠α
Im
A = a + jb
b
onde
A = a 2 + b2
"b%
α = tan −1 $ '
#a&
A
α
a
Re
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: A = 4 + j 3
A = 42 + 32 = 5
( )
α = tan −1 3 = 36,9°
4
A = 5∠36,9°
Exemplo: A = -5 -j 12
Im
A=
2
(−5) + (−12)
2
( )
= 13
α = 180º+ tan −1 −12 = 247,4°
−5
-5
α
Re
A
A = 13∠247,4°
A = −5 − j12
-12
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Outras relações úteis:
j = 1∠90°
j 2 = −1 = 1∠180°
Fórmula de Euler:
Vm cos ω t + jVm sen ω t = Vme jω t
( )
( )
Re Vme jω t = Vm cos ω t
{
}
( )
Im Vme jω t = Vm sen ω t
{
}
( )
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Retomando o exemplo do circuito RL:
R
vg = Vm cos(ωt)
+
-
R
i
L
v1 = Vm ejωt
+
-
i1
L
Seja v1 = Vmejωt a excitação complexa do circuito, então
vg = Vm cos(ωt) = Re{v1}
Componente forçada da corrente i1 na forma complexa deve resolver a equação:
L
di1
+ Ri1 = v1
dt
onde v1 = Vme jω t
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Para resolver a equação vamos tentar:
i1 = Ae jω t
Então,
L
Logo,
di1
+ Ri1 = Vme jω t
dt
jω LAe jω t + RAe jω t = Vme jω t
( jω L + R) Ae jωt = Vme jωt
Vm
A=
R + jω L
=
Vm
2
2 2
R +ω L
e
"ω L %
− j tan −1$
'
# R &
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Então:
i1 = Ae jω t
i1 =
"ω L % +
(
− j tan −1$
'
Vm
*
# R & - jω t
=
e
e
* 2
2 2
*) R + ω L
-,
Vm
2
2 2
e
(
" ω L %+
j*ω t−tan −1$
'# R &,
)
R +ω L
mas if = Re{i1}, assim
(
" ω L %+ 2
.
j*ω t−tan −1$
'0
Vm
# R &, 0
)
i f = Re /
e
3=
2
2
2
0 R +ω L
0
1
4
(
"
%+
−1 ω L
cos *ω t − tan $
'2
2 2
R
#
&,
)
R +ω L
Vm
Portanto, se i1 é a resposta complexa para a função excitação complexa v1,
então if = Re{i1} é a resposta para a excitação vg = Re{v1}.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Note que:
! di
$
1
Re " L + Ri1 % = Re Vme jω t
# dt
&
{
}
pode ser escrita como:
L
d
Re {i1} + R Re {i1} = Vm cos ω t
dt
(
) (
)
( )
e, portanto, de
L
di
+ Ri = Vm cos ω t
dt
( )
temos:
i = i f = Re {i1}
Portanto, é mais fácil usar a função excitação complexa v1 para encontrar a
resposta complexa i1.
A função excitação real é Re{v1} ⇒ a resposta real é Re{i1}.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
10.4 Excitações Complexas
Sem perda da generalidade, vamos considerar a entrada como sendo uma fonte
de tensão e a saída como sendo uma corrente através de um elemento.
Em geral, a excitação é da forma:
(
v g = Vm cos ω t + θ
)
Enquanto que a resposta forçada é da forma:
(
i = i f = I m cos ω t + φ
)
Portanto, sabendo-se os valores de ω, θ e Vm, podemos calcular Im e φ.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
(
v g = Vm cos ω t + θ
)
+
-
Circuito
(
i = I m cos ω t + φ
Para resolver i no circuito, vamos considerar a excitação complexa:
j ω t+θ
v1 = Vme ( )
v1 = Vme (
j ω t+θ
)
+
-
Pois sabemos que i = Re {i1}
Circuito
i1
)
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
A equação representativa do circuito pode ser resolvida para a resposta forçada,
visto que
v1 = Vme jθ e jω t
a solução tentativa é:
i1 = Ae jω t
(
Comparando i = I m cos ω t + φ
)
com i = Re {i1}, temos
I m cos ω t + φ = Re Ae jω t
Assim,
(
{
)
}
A = I me jφ
e
jφ
i1 = I me e
jω t
Re{ }
(
i = I m cos ω t + φ
)
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Cálculo da resposta forçada if de
d 2i
+2
2
di
+ 8i = 12 2 cos 2t +15°
dt
(
dt
Troca para a excitação complexa:
)
j 2t+15°)
v1 = 12 2e (
Resposta complexa i1 deve satisfazer:
d 2i1
+2
di1
j 2t+15°)
+ 8i1 = 12 2e (
dt
dt 2
Então, i1 pode ter a seguinte forma:
i1 = Ae j2t
Substituindo, obtemos
d2
dt 2
(
)
Ae j2t + 2
j 2t+15°)
d
Ae j2t + 8 Ae j2t = 12 2e (
dt
(
) (
)
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Assim,
(−4 + j4 + 8) Ae j2t = 12
2e j15°e j2t
Logo,
12 2e j15° 12 2∠15°
A=
=
= 3∠ − 30°
4 + j4
4 2∠45°
Portanto,
j 2t−30°)
i1 = Ae j2t = 3∠ − 30° e j2t = 3e (
(
)
E a resposta real é:
j 2t−30°)
i = Re {i1} = Re 3e (
{
} = 3cos (2t − 30°)
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exercício: Calcular a resposta forçada v:
10 Ω
a)
i
vg = 10e
j8t
[V]
+
-
1/20 F
5 Ω
v − vg
10
+i +
1 dv
=0
20 dt
5i = v
v − vg
v 1 dv
+ +
=0
10
5 20 dt
dv
+ 6v = 2v g
dt
dv
+ 6v = 20e j8t
dt
+
v
-
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Resposta forçada:
v = Ae j8t
dv
+ 6v = 20e j8t
dt
j8Ae j8t + 6Ae j8t = 20e j8t
(6 + j8) Ae j8t = 20e j8t
A=
20
20∠0°
=
= 2∠ − 53,1°
6 + j8 10∠53,1°
j 8t−53,1°)
v = 2e − j53,1°e j8t = 2e (
b) Se vg = 10 cos(8t) [V], então:
j 8t−53,1°)
v = Re 2e (
{
} = 2cos (8t − 53,1°)
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
10.5 Fasores
Fasores permitem colocar os resultados obtidos anteriormente em uma forma
mais compacta.
Tensão senoidal:
(
v = Vm cos ω t + θ
)
Forma fasorial
V = Vme jθ = Vm∠θ
Razão para a definição de fasor (fórmula de Euler):
Vm cos ω t + θ = Re Vme jθ e j ω t
(
)
{
Assim,
v = Re Ve j ω t
{
}
}
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
(
)
Exemplo: Dado v = 10cos 4t + 30°
!V#
" $
Representação fasorial:
V = 10∠30° "#V$%
Visto que ω = 4 rad/s, v é prontamente obtida de V.
Representação fasorial para corrente:
(
)
i = I m cos ω t + φ
I = I me jφ = I m∠φ
Exemplo: Dado ω = 6 rad/s, e I = 2∠15º, então temos:
(
)
i = 2cos 6t +15°
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Representação fasorial para tensão e corrente é feita a partir da representação
temporal na forma de cosseno.
(
)
Exemplo: Dada a função: v = 8sen 3t + 30°
!V#
" $
Podemos mudá-la para:
(
= 8cos (3t − 60°)
)
v = 8cos 3t + 30° − 90°
Assim, a representação fasorial é:
V = 8∠ − 60° #$V%&
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo:
vg = Vm cos(ωt)
R
+
-
L
i
L
di
+ Ri = Vm cos ω t
dt
( )
v1 = Vme jω t = Ve jω t
pois θ = 0 e portanto, V = Vm ∠0º. Substituindo este valor e fazendo i = i1 na
equação representativa, temos:
L
onde i = Re{i1}
di1
+ Ri1 = Ve jω t
dt
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Tentando a solução: i1 = Ie jω t
obtemos:
jω LIe jω t + RIe jω t = Ve jω t
jω LI + RI = V
Assim,
Vm∠0º
V
I=
=
R + jω L
#ω L &
R 2 + ω 2 L2 ∠tan −1 %
(
$ R '
Substituindo na expressão de i1, obtemos
i1 =
=
#ω L &
∠ − tan %
(
2
2 2
R
$
'
R +ω L
.0 (
"
%+2
−1 ω L 0
exp / j *ω t − tan $
'-3
2
2 2
R
01 )
#
&,04
R +ω L
Vm
Tomando a parte real desta expressão temos:
i=
Vm
(
"
%+
−1 ω L
cos *ω t − tan $
'2
2 2
R
#
&,
)
R +ω L
Vm
−1
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Note que podemos ir da equação característica do circuito:
L
di
+ Ri = Vm cos ω t
dt
( )
direto para a equação fasorial:
jω LI + RI = V
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
10.6 Relações Tensão-Corrente para Fasores
Tensão-Corrente para resistores:
v = Ri
onde
(
)
(
)
v = Vm cos ω t + θ
i = I m cos ω t + φ
Tensão e corrente complexas:
v1 = Vme j (ω t +θ )
i1 = I me j (ω t +φ )
Substituindo na lei de Ohm e eliminando o fator e jωt:
j ω t+θ )
j ω t+φ )
Vme (
= RI me (
Vme jθ = RI me jφ
V = RI
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Da equação:
Vme jθ = RI me jφ
podemos verificar que
Vm = RI m
θ =φ
Portanto, a tensão e a corrente senoidais para um resistor possuem o mesmo
ângulo de fase, isto é, estão em fase.
v,i
v
i
t
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: R = 5 Ω, v = 10 cos(100t + 30º) [V]
I
i
+
v
+
R = 5 Ω
V = RI
-
-
V = 10∠30° "#V$%
I=
V 10∠30°
=
= 2∠30° "#A$%
R
5
No domínio do tempo:
(
)
i = 2cos 100t + 30°
! A#
" $
R = 5 Ω
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Tensão-Corrente para indutores:
i
I
+
+
v = Ldi/dt
L
-
V = jωLI
-
v=L
di
dt
j ω t+θ )
Tensão e corrente complexas: v1 = Vme (
j ω t+φ )
i1 = I me (
j ω t+θ
j ω t+φ ) $
j (ω t+φ )
d!
Vme ( ) = L # I me (
=
j
ω
LI
e
&%
m
dt "
Vme jθ = jω LI me jφ
V = jω LI
j ωL
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
(
Se a corrente no indutor é dada pela a equação i = I m cos ω t + φ
)
Então, como j = 1∠90º, temos:
(
V = jω LI = jω L I m∠φ
(
)
)
= ω L I m∠φ + 90°
(
)
Portanto, no domínio do tempo temos: v = ω LI m cos ω t + φ + 90°
Comparando com i = I m cos(ωt + φ ) , verificamos que a corrente pelo indutor está
atrasada da tensão de 90º.
v,i
v
i
t
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Tensão-Corrente para capacitores:
I= jωCV
i = Cdv/dt
+
+
v
C
-
V
1/jωC
-
i = C dv
dt
j ω t+θ )
Tensão e corrente complexas: v1 = Vme (
j ω t+φ )
i1 = I me (
j ω t+φ )
j ω t+θ ) $
j (ω t+θ )
d!
I me (
= C #Vme (
=
j
ω
CV
e
&%
m
dt "
I me jφ = jωCVme jθ
I = jωCV
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
(
)
Se a tensão no capacitor é dada pela a equação v = Vm cos ω t + θ
Então, como j = 1∠90º, temos:
(
I = jωCV = jωC Vm∠θ
(
)
)
= ωCVm∠ θ + 90°
Portanto, no domínio do tempo temos:
(
(
)
i = ω CVm cos ω t + θ + 90°
)
Comparando com v = Vm cos ω t + θ , verificamos que a corrente pelo capacitor
está adiantada da tensão de 90º.
v,i
v
i
t
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
(
)
Exemplo: Capacitor C = 1 µF e tensão igual a v = 10cos 100t + 30°
i = Cdv/dt
+
v
C = 1 µF
-
)(
)(
I = j ω C V = j100 ⋅ 10−6 ⋅ 10∠30°
(
= 1∠120°
)
$ A&
% '
$mA&
%
'
Corrente no domínio do tempo:
(
)
i = cos 100t +120°
!mA#
"
$
!V#
" $
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
10.7 Impedância e Admitância
Circuito geral com grandezas fasoriais:
I
+
Circuito
Fasorial
V
_
V = Vm∠θ
I = I m∠φ
Impedância Z do circuito:
Z=
Z = Z ∠θ z =
Vm
∠ θ −φ
Im
(
)
V
I
[Ω]
Vm
Z=
Im
θz = θ − φ
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Impedância Z segue as mesmas regras dos resistores em circuitos.
A impedância é um número complexo mas não é um fasor.
Impedância na forma retangular:
Z = R + jX
onde
R = Re{Z} = componente resistiva (resistência)
X = Im{Z} = componente reativa (reatância)
Em geral, Z = Z(jω) é uma função complexa de jω mas R = R(ω) e X = X(ω) são
funções reais de ω.
Note que
Z = R2 + X 2
" %
−1 X
θ z = tan $ '
#R&
|Z|
X
θz
R
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: V = 10∠56,9º e I = 2∠20º
I
+
Circuito
Fasorial
V
_
Z=
V 10∠56,9°
=
= 5∠36,9°
I
2∠20°
#Ω%
$ &
Forma retangular:
Z = 5!"cos 36,9° + j sen 36,9° #$
(
)
= 4 + j3
!Ω#
" $
(
)
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Impedância Z de resistores, indutores e capacitores:
ZR = R
Z L = jω L
ZC =
1
1
1
=−j
=
∠ − 90°
jω C
ωC ωC
No caso do resistor, a impedância é puramente resistiva, sendo a reatância
zero.
No caso do indutor e do capacitor, a impedância é reatância pura, sem
componente resistiva.
Reatância indutiva:
X L =ωL
Reatância capacitiva: X C = − 1
ωC
Z L = jX L
ZC = jX C
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
A reatância indutiva é positiva e a reatância capacitiva é negativa.
No caso geral, Z = R + jX podemos ter as seguintes situações:
•  X = 0 ⇒ circuito resistivo.
•  X > 0 ⇒ circuito indutivo.
•  X < 0 ⇒ circuito capacitivo.
A recíproca da impedância é chamada de admitância:
Y=
1
Z
Y = G + jB
onde G = Re{Y} é a condutância e B = Im{Y} é a susceptância.
Y = G + jB =
1
1
=
Z R + jX
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Relação entre as componentes de Y e Z:
# R − jX &
%×
(
R
−
jX
$
'
1
G + jB =
R + jX
G + jB =
Assim,
G=
R − jX
R2 + X 2
=
R
R2 + X 2
R
R2 + X 2
B=−
X
R2 + X 2
Importante: R e G (X e B) não são recíprocos!!!
G=
1
R
B=
1
X
−j
X
R2 + X 2
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Z = 4 + j 3
Então,
Y=
1
4 − j3 4
3
= 2 2= −j
4 + j3 4 + 3
25
25
Portanto,
G=
4
25
B=−
3
25
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
10.8 Leis de Kirchhoff e Associações de Impedâncias
As leis de Kirchhoff são válidas para fasores, assim como para as tensões e
correntes correspondentes no domínio do tempo.
A lei de Kirchhoff de tensões aplicada em um laço típico resulta na equação:
j ω t+θ
j ω t+θ
j ω t+θ N )
V1e ( 1 ) +V2e ( 2 ) +!+VN e (
=0
Dividindo por e jω t, temos:
V1e
jθ1
+V2e
jθ 2
+!+VN e
jθ N
=0
ou seja,
V1 + V2 +!+ VN = 0
onde
Vn = Vn∠θ n ,
n = 1, 2,!, N
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
A lei de Kirchhoff de correntes aplicada em um nó típico resulta na equação:
j ω t+φ
j ω t+φ
j ω t+φ
I1e ( 1 ) + I 2e ( 2 ) +!+ I N e ( N ) = 0
Dividindo por e jω t, temos I1e
jφ1
+ I 2e
jφ2
+!+ I N e
jφ N
= 0 , ou seja,
I1 + I 2 +!+ I N = 0
onde
I n = I n∠φn ,
n = 1, 2,!, N
Se as excitações são senoidais com frequência comum em um circuito,
podemos encontrar as tensões e correntes fasoriais para todos os elementos e
utilizar as leis de Kirchhoff para a análise.
A análise em regime permanente c.a. é idêntica à análise para circuitos
resistivos, com a impedância no lugar da resistência.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo:
I
+
V
Z1
Z2
ZN
+ V1 -
+ V2 -
+ VN -
V1 = Z1I
V2 = Z 2I
VN = Z N I
-
Zeq
Lei de Kirchhoff de tensões:
V = V1 + V2 +!+ VN
(
)
V = Z1 + Z 2 +!+ Z N I
V = Z eq I
Z eq = Z1 + Z 2 +!+ Z N
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
De maneira análoga, temos para N admitâncias em paralelo:
I
+
V
I1
I2
IN
Y1
Y2
YN
I1 = VY1
I 2 = VY2
I N = VYN
-
Yeq
Lei de Kirchhoff de correntes:
I = I1 + I 2 +!+ I N
(
)
I = Y1 + Y2 +!+ YN V
I = Yeq V
Yeq = Y1 + Y2 +!+ YN
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
No caso particular de apenas dois elementos em paralelo, temos:
Z eq =
ZZ
1
1
=
= 1 2
Yeq Y1 + Y2 Z1 + Z 2
Obs.: Regras de divisão de tensão e de corrente também são válidas para
circuitos fasoriais, com a impedância e as quantidades no domínio da
frequência.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Circuito RL.
R
vg = Vm cos(ωt)
+
-
R
i
L
Vm ∠0º
+
-
Lei de Kirchhoff de tensões no circuito fasorial:
RI + Z LI = Vm∠0°
( R + jω L) I = Vm∠0°
I=
Vm∠0°
=
R + jω L
Vm
#ω L &
∠ − tan −1 %
(
2
2 2
R
$
'
R +ω L
I
j ωL
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
No domínio do tempo:
I=
i=
Vm
#ω L &
∠ − tan %
(
2
2 2
R
$
'
R +ω L
−1
(
"
%+
−1 ω L
cos *ω t − tan $
'2
2 2
R
#
&,
)
R +ω L
Vm
Método alternativo de solução:
Impedância vista pelos terminais da fonte é:
I
Z = R + jω L
V
e a corrente:
I=
como obtida anteriormente.
V Vm∠0°
=
Z R + jω L
R
+
-
j ωL
Z
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
10.9 Circuitos Fasoriais
Equação representativa de um circuito fasorial é uma equação fasorial.
Resolvendo esta equação obtemos uma resposta na forma de fasor, que é
convertida para uma resposta no domínio do tempo.
Exemplo: Cálculo de i no circuito.
i1
i
1Ω
3Ω
vg = 5 cos(3t)
+
-
1/9 F
1H
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
I1
I
1Ω
3Ω
5∠0º
+
-
-j3 Ω
j3 Ω
Impedância vista dos terminais da fonte:
3+ j3) (− j3)
(
Z = 1+
= 4 − j3
3+ j3− j3
Portanto, temos:
I1 =
5∠0°
5∠0°
=
= 1∠36,9°
4 − j3 5∠ − 36,9°
Por divisão de corrente, temos:
3+ j3
I=
I1 = 1+ j ⋅ 1∠36,9° =
3+ j3− j3
(
)(
)
(
(
)(
)
2∠45° ⋅ 1∠36,9° = 2∠81,9°
)
Corrente no domínio do tempo: i = 2 cos 3t + 81,9°
! A#
" $
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Cálculo de i no circuito com fonte de tensão dependente.
1/8 F
a
i
3cos(4t) [A]
+
4Ω
v1
+
-
(1/2)v1
+
-
(1/2)V1
-
-j2 Ω
a
I
+
3∠0º [A]
V1
4Ω
-
Lei de Kirchhoff de correntes em a:
1
V1 − V1
2 = 3∠0°
I+
− j2
1
V1
2
I+
= 3∠0°
− j2
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Pela lei de Ohm, temos V1 = 4I, logo
1
4I
I + 2 = 3∠0°
− j2
− j2I + 2I = − j6
I=
Portanto, temos:
− j6
6∠ − 90°
3
=
=
∠ − 45°
2 − j2 2 2∠ − 45°
2
i=
3
2
(
)
cos 4t − 45°
" A$
# %
Obs.: O método fasorial de obter i, calculando primeiramente I = V/Z e
trocando I por i, não funciona se Z(jω) = 0. Pois, neste caso, o circuito é
excitado na frequência natural jω.