Aula 20

ENG04030
ANÁLISE DE CIRCUITOS I
Aulas 20 – Circuitos de 1ª
1ª ordem: aná
análise no
domí
domínio do tempo
Capacitores e indutores em regime permanente CC;
circuitos divisores de corrente e de tensão em
capacitores e indutores
Sérgio Haffner
A tensão nos terminais de um indutor de 2H é 6cos5t
6cos5t.
Determine a corrente neste indutor (convenç
(convenção passiva)
sabendo que i(−π/2)= 1A.
1A.
Calcule a má
máxima energia armazenada
no indutor da figura e a quantidade
de energia dissipada no
resistor durante o tempo
em que a energia
está
está sendo
armazenada
no indutor.
SHaffner2010 – [email protected]
Exercícios
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
1
Exercícios – resultado 1/2
A tensão nos terminais de um indutor de 2H é 6cos5t
6cos5t.
Determine a corrente neste indutor (convenç
(convenção passiva)
sabendo que i(−π/2)= 1A.
1A.
SHaffner2010 – [email protected]
Resultado via Microcap:
Microcap: aula20a.cir
aula20a.cir
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
Exercícios – resultado 2/2
Calcule a má
máxima energia armazenada no indutor da
figura e a quantidade de energia dissipada no
resistor durante o tempo em que a energia está
está
sendo armazenada no indutor.
SHaffner2010 – [email protected]
Resultado via Microcap:
Microcap: aula20b.cir
aula20b.cir
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
2
SHaffner2010 – [email protected]
Exercício
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
Exercício – resultado 1/2
SHaffner2010 – [email protected]
Resultado via Microcap:
Microcap: aula20c.cir
aula20c.cir
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
3
Exercício – resultado 2/2
SHaffner2010 – [email protected]
Resultado via Microcap:
Microcap: aula20c.cir
aula20c.cir
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
(c) 126µJ
SHaffner2010 – [email protected]
Exercício
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
4
Exercício – resultado 1/2
SHaffner2010 – [email protected]
Resultado via Microcap:
Microcap: aula20d.cir
aula20d.cir
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
Exercício – resultado 2/2
SHaffner2010 – [email protected]
Resultado via Microcap:
Microcap: aula20d.cir
aula20d.cir
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
5
Capacitores e indutores em regime
permanente CC
Caso todas as fontes do circuito sejam contí
contínuas (com
valor constante) temtem-se:
= lim iC ( t )
t →∞
vC ( ∞ ) = lim
t →∞
 dv ( t ) 
= lim C
= 0
t →∞ 
dt 
1 t
i (τ ) dτ + vC ( t0 ) = constante
C ∫t0
comportacomporta-se como um circuito aberto
tensão e carga são constantes (não são necessariamente nulos)
Indutor
vL ( ∞ ) = lim vL ( t )
t →∞
iL ( ∞ )
= lim
t →∞
 di ( t ) 
= lim  L
= 0
t →∞ 
dt 
1 t ( )
v τ dτ + iL ( t0 ) = constante
L ∫t0
comportacomporta-se como um curtocircuito
corrente e fluxo são constantes (não são necessariamente nulos)
SHaffner2010 – [email protected]
Capacitor i ( ∞ )
C
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
Exercício
Supondo que o circuito se encontra em regime permanente CC e que
V=120 V,
V, determinar:
SHaffner2010 – [email protected]
o circuito equivalente para o regime permanente CC
o valor de regime das tensões e correntes nos indutores e capacitores
capacitores
a potência fornecida pela fonte em regime permanente
a energia total armazenada no circuito
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
6
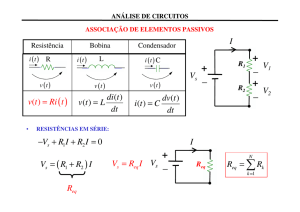
Divisor de corrente em capacitores
Para a associaç
associação paralela de capacitores,
capacitores, temtem-se:
=
dv ( t )
dt
=
is ( t )
C1 + C2 + K + CN
logo, a corrente em um capacitor qualquer é dada por:
i1 ( t ) = C1
dv ( t )
dt
= is ( t )
C1
C1 + C2 + K + CN
SHaffner2010 – [email protected]
dv ( t )
dv ( t )
dv ( t )
+ C2
+ K + CN
dt
dt
dt
(
)
dv t
= ( C1 + C2 + K + C N )
dt
is ( t ) = C1
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
Divisor de tensão em capacitores
Para a associaç
associação sé
série de capacitores,
capacitores, temtem-se:
1 t ( )
1
i τ dτ + v1 ( t0 ) +
C1 ∫t0
C2
∫
t
t0
i (τ ) dτ + v2 ( t0 ) + K +
1
CN
∫
t
t0
i (τ ) dτ + vN ( t0 ) =
1
1  t ( )
 1
=  +
+K +
 ∫t0 i τ dτ + v1 ( t0 ) + v2 ( t0 ) + K + vN ( t0 )
C
C
C
N 
 1
2
vs ( t ) − v1 ( t0 ) + v2 ( t0 ) + K + vN ( t0 ) 
t
∫ i (τ ) dτ =
1
1
1
+
+K +
C1 C2
CN
t0
logo, a tensão em um capacitor qualquer é dada por:
1 t
v1 ( t ) =
i (τ ) dτ + v1 ( t0 ) =
C1 ∫t0
{v ( t ) − v ( t ) + v ( t ) + K + v
s
1
0
2
0
N
( t0 )}
1
C1
1
1
1
+
+K +
C1 C2
CN
+ v1 ( t0 )
SHaffner2010 – [email protected]
vs ( t ) =
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
7
Divisor de tensão em indutores
Para a associaç
associação sé
série de indutores,
indutores, temtem-se:
=
di ( t )
dt
=
SHaffner2010 – [email protected]
di ( t )
di ( t )
di ( t )
+ L2
+ K + LN
dt
dt
dt
(
)
di t
= ( L1 + L2 + K + LN )
dt
vs ( t ) = L1
vs ( t )
L1 + L2 + K + LN
logo, a tensão em um indutor qualquer é dada por:
v1 ( t ) = L1
di ( t )
dt
= vs ( t )
L1
L1 + L2 + K + LN
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
Divisor de corrente em indutores
Para a associaç
associação paralela de indutores,
indutores, temtem-se:
is ( t ) =
1 t ( )
1
v τ dτ + i1 ( t0 ) +
L1 ∫t0
L2
∫
t
t0
v (τ ) dτ + i2 ( t0 ) + K +
1
LN
∫
t
t0
v (τ ) dτ + iN ( t0 ) =
∫
t
t0
v (τ ) dτ
=
is ( t ) − i1 ( t0 ) + i2 ( t0 ) + K + iN ( t0 ) 
1 1
1
+ +K +
L1 L2
LN
logo, a corrente em um indutor qualquer é dada por:
i1 ( t ) =
1 t
v (τ ) dτ + i1 ( t0 ) =
L1 ∫t0
{i ( t ) − i ( t ) + i ( t ) + K + i
s
1
0
2
0
N
( t0 ) }
1
L1
1 1
1
+ +K +
L1 L2
LN
+ i1 ( t0 )
SHaffner2010 – [email protected]
1  t ( )
1 1
=  + +K +
v τ dτ + i1 ( t0 ) + i2 ( t0 ) + K + iN ( t0 )
LN  ∫t0
 L1 L2
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
8
Exercício
Sabendo que as cargas armazenadas nos capacitores
antes da abertura da chave são todas iguais a 60µ
60µC,
determinar:
t=0
100 V
+
−
+
2 µF
4 µF
v2 ( t )
6 µF
−
− v3 ( t ) +
SHaffner2010 – [email protected]
a tensão em v2(t) instantes apó
após o fechamento da chave
a carga armazenada em cada capacitor instantes apó
após o
fechamento da chave
+ v1 ( t ) −
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
Exercício (suposto paradoxo)
a tensão nos capacitores apó
após o fechamento da chave
a carga armazenada em cada capacitor antes e apó
após o
fechamento da chave
a energia armazenada nos capacitores antes e apó
após o fechamento
da chave
+
v1 ( t )
+
t =0
C1
C2
−
v2 ( t )
−
SHaffner2010 – [email protected]
No circuito a seguir, considere que C1=C2=C e que antes
de fechar a chave o capacitor C2 está
está descarregado e a
tensão em C1 é de V. Determinar:
ENG04030 - ANÁ
ANÁLISE DE CIRCUITOS I
9