Aula 12

Circuitos de 1ª ordem
Parte 2
Resposta a um degrau de circuitos
RL
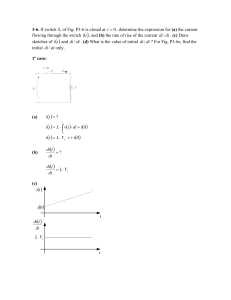
Circuito RL com aplicação de um degrau de tensão
• VS = Ri + L di/dt
Resposta ao degrau
• Por separação de variáveis temos:
(di/dt) = (-Ri + Vs)/L = (-R/L)(i-Vs/R)
di/(i-Vs/R)= (-R/L) dt
Integrando:
i (t )
t
∫ dx x − (V
I0
s / R)
= − R / L ∫ dy
0
Solução da equação diferencial
ln
i(t ) − V s / R
I 0 − V s / R
i(t ) − V s / R
I 0 − V s / R
Solução
i(t ) =
=
=
e
( − R / L )t
( − R / L ) t
:
V s
R
+ ( I
0
V s
−
)e
R
( − R / L ) t
• Quando energia inicial no indutor é zero temos:
Vs Vs −( R / L ) t
i (t ) = − e
R R
• Uma cte de tempo depois da chave ter sido fechada, a corrente terá
alcançado aproximadamente 63% de seu valor final, ou
i(τ) =Vs/R – (Vs/R) e-1=0,6321 Vs/R
• Se a corrente continuasse a aumentar à sua taxa inicial, alcançaria
seu valor final em t=τ, isto é, como
di/dt=(-Vs/R)(-1/τ)e-t/τ = (Vs/L)e-t/τ,
• A taxa de variação inicial de i(t) é Vs/L
• Se a corrente continuasse a aumentar a essa taxa, a expressão de
corrente seria
i=(Vs/L) t
Gráfico de i(t) – circuito RL série
A expressão de tensão
• A tensão no indutor é Ldi/dt, logo:
v=(Vs-I0R)e-(R/L)t
Quando I0=0, temos:
v=Vse-(R/L)t
Exemplo 1
• Tendo o circuito abaixo, encontre o gráfico de i(t) e v(t).
• A corrente inicial( chave em a) no indutor pelo circuito acima é -8 A.
• Quando a chave estiver em b, a corrente final será 24/2=12 A.
• A cte é 200 10-3/2 = 10ms. Logo:
• i(t) =12 +(-8-12)e-t/0,1= 12-20e-10t A, t≥0
• A tensão no indutor:
v=(24 + 8x2)e-10t = 40e-10t V, t≥0+
A tensão inicial é 40 V
Resposta ao degrau de um circuito
RC
CdVc/dt + vc/R = Is
• Comparando com a resposta do indutor temos:
vc = IsR + ( V0 – IsR)e-t/RC, t≥0
A expressão de corrente
i= C dv/dt
i=(Is – V0/R)e-t/RC, t≥0+
Exemplo 2
•
Calcule i0(t) e v0(t) quando a chave passa para a posição 2. A
chave esteve na posição 1 por longo tempo.
• O valor de v0 inicial ( chave posição 1) é 40(60/80) ou 30V.
• Para usarmos as equações de tensão e corrente vistas
anteriormente temos que encontrar o equivalente de Norton.
• V0C = Vth =(-75)160 103/(40+160)103=-60V
• Rth=8000+40000//160000 = 40kΩ
• O circuito de Norton é:
• RC=10ms
Já sabemos que:v0=IR+(V0-IR)e-t/RC
v0=-60 + [30 –(-60)]e-100t
v0= -60+90e-100t , t≥0
i0=(-1,5 -0,75)e-100tmA, t≥0+
Solução geral para respostas a um
degrau e natural
• Analisando as respostas vistas até a agora podemos
visualizar que a resposta geral para qualquer
configuração é na forma abaixo:
Variável desconhecida=valor final da variável
+[valor inicial – valor final]e-(t-tchaveamento)/cte tempo
Resposta completa= resposta transitória + resposta permanente
Etapas de cálculo das respostas
• Identificar a variável de interesse
• Determinar o valor inicial da variável
• Calcular o valor final da variável
• Calcular a cte de tempo
Exemplo 3
• Faça o gráfico de vc e i do circuito abaixo
A tensão inicial do capacitor é a tensão do
resistor de 60 ohms, ou seja,
-40x[60/(60+20)], ou -30 V
Após a chave ser colocada para b por um
longo tempo a tensão no capacitor é 90V.
• A cte de tempo é 400 103 x 0,5 10-6=0,2 s
vc(t)=90 +(-30-90)e-5t
vc(t)=90-120e-5t, t≥0
A corrente é dada por:
i(t) = ifinal + ( iinicial – ifinal) e-5t
ifinal =0
iinicial=[90 –(-30)]/400 103=300µA
• i(t) = 300e-5tµA, t≥0+
Respostas a outras entradas
Entrada
Resposta
Me-bt
Ne-bt
Msen(ωt+θ)
Asenωt + Bcosωt
Resposta a uma entrada impulsiva
Para se obter a resposta a um impulso,
basta derivar a resposta ao degrau.