t - DECOM

EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Capítulo 8
Circuitos Simplificados RC e RL
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
8.1 Circuitos RC sem Fontes
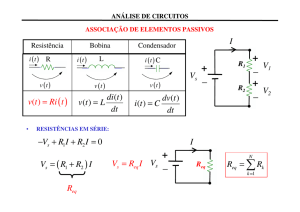
Associação em série de um resistor e um capacitor:
i(t)
+
v(t)
−
C
R
Capacitor carregado com tensão V0 em t = 0.
Energia em t = 0:
1
w(0 ) = CV02
2
Aplicando Lei de Kirchhoff de correntes quando t ≥ 0, temos:
C
dv v
+ =0
dt R
dv
1
+
v=0
dt RC
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Solução da equação diferencial de 1ª ordem:
dv
1
+
v=0
dt RC
dv
1
=−
dt
v
RC
dv
1
=
−
dt
∫v
RC ∫
ln v = −
t
+K
RC
Para que a solução seja válida para t ≥ 0, a constante K deve ser escolhida tal
que a condição inicial de v(0) = V0 seja satisfeita, Portanto, em t = 0, temos:
ln v(0 ) = ln V0 = K
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Substituindo o valor de K na solução, temos:
ln v = −
t
t
+K =−
+ ln V0
RC
RC
ln v − ln V0 = −
ln
t
RC
v
t
=−
V0
RC
 t 
v(t ) = V0 exp −

RC


Esta é a tensão sobre R, portanto, a corrente é:
i(t ) =
v(t ) V0
 t 
= exp −

R
R
RC


EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
v(t)
V0
t
Observe que a tensão é inicialmente V0 e que decai exponencialmente,
tendendo a 0, para t crescente.
Velocidade de decaimento da tensão é determinada pelo produto RC.
Como a resposta é caracterizada pelos elementos do circuito e não pela
atuação de uma fonte externa de tensão e corrente, a resposta é denominada
de resposta natural do circuito.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Potência instantânea absorvida pelo resistor R:
v 2 (t ) V02
 2t 
exp −
pR (t ) =
=

R
R
 RC 
[W ]
Energia absorvida pelo resistor para t → ∞ é:
∞
wR (∞ ) = ∫ pR (t )dt
0
2
∞ V0
 2t 
exp −
=∫
dt
0 R
 RC 
 2t 
= − 1 CV02 exp −

2
∞
 RC  0
= 1 CV02
2
energia armazenada no circuito
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Se o tempo inicial é t0, isto é, v(t0) = V0, então
 t − t0 
v(t ) = V0 exp −

RC


para t ≥ t0
8.2 Constante de Tempo
Caracterização da velocidade de decaimento de um circuito com elementos
armazenadores.
i(t)
 t 
v = V0 exp −

 RC 
+
v(t)
−
C
R
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Gráfico v(t) × t:
 t 
v = V0 exp − 
 nk 
v(t)
V0
RC = k
RC = 2k
RC = 3k
0,368V0
1
2
3
t/k
Corrente no circuito decresce como a tensão:
V
 t 
i(t ) = 0 exp −

R
 RC 
O tempo necessário para que a resposta natural decaia de um fator de 1/e é
definido como a constante de tempo τ do circuito.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
 (t + τ )  V0
 t 
 t

 (t + RC ) 
V0 exp −
− 1 = V0 exp −
 = e exp −
 = V0 exp −

RC
RC
RC
RC








 (t + τ ) 
 (t + RC ) 
V0 exp −

 = V0 exp −
RC 
 RC 

Constante de tempo: τ = RC
Unidade de τ : (Ω⋅F) = (V/A)⋅(C/V) =( C/A) = s
Tensão:
 t
v(t ) = V0 exp − 
 τ
A resposta ao final de 1 constante de tempo é reduzida para e−1 = 0,368 do
valor inicial. Ao final de 2 constantes de tempo, ela é igual a e−2 = 0,135 do seu
valor inicial e depois de 5 constantes, ela é igual a e−5 = 0,0067.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Propriedade das funções exponenciais:
v(t)
v
V0
v1
0,368V0
τ
t
Tangente à curva em t = 0 intercepta o eixo de t em t = τ.
v1 = mt + V0
dv d 
V
 t 
 t
= V0 exp −  = − 0 exp − 
dt dt 
τ
 τ 
 τ
m=
dv
V
=− 0
dt t =0
τ
V
v1 = − 0 t + V0
τ
A reta intercepta o eixo do tempo em v1 = 0, o que requer que t = τ.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
A constante de tempo é o tempo necessário para que a resposta natural se
torne zero se ela decrescer com uma velocidade constante igual à razão inicial
de decréscimo.
A constante de tempo permite predizer a forma geral da resposta:
 t
v(t ) = V0 exp − 
 τ
mas para a solução completa deve-se encontrar a tensão inicial v(0+) = V0.
Para um capacitor: v(0−) = v(0+) = V0.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
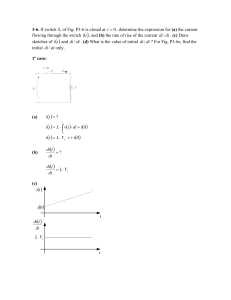
Exemplo: Tensão no capacitor v(t). Circuito em regime permanente cc
imediatamente antes da abertura da chave.
4Ω
3Ω
2Ω
15 Ω
8Ω
t=0
+
+
v(t)
v1(t)
−
−
1F
100 V
Em t = 0−, chave fechada ⇒ capacitor é um circuito aberto.
4Ω
2Ω
15 Ω
8Ω
3Ω
+
v1(t)
−
v(0-)
t = 0-
+
−
Req
100 V
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Req = 8 +
( )
v 0− =
3(2 + 4 )
= 10 [Ω ]
3 + (2 + 4 )
10
× 100 = 40 [V ]
10 + 15
Portanto, v(0-) = v(0+) = V0 = 40 [V].
Para t > 0, temos:
Constante de tempo: τ = ReqC = 10 [s ]
+
Req = 10 Ω
v(t)
−
1F
 t
 t 
v(t ) = V0 exp −  = 40 exp −  [V ]
 τ
 10 
v1(t ) =
2
 t 
v(t ) = 8 exp −  [V ]
2+8
 10 
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
8.3 Circuitos RL sem Fontes
Associação em série de um resistor e um indutor:
i(t)
+
v(t)
−
L
R
Indutor está conduzindo uma corrente I0 em t = 0.
Energia em t = 0:
1
w(0 ) = L ⋅ I 02
2
Aplicando Lei de Kirchhoff de tensões quando t ≥ 0, temos:
L
di
+ Ri = 0
dt
di R
+ i=0
dt L
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Solução 1: Solução da equação diferencial de 1ª ordem por separação de
variáveis:
di R
+ i=0
dt L
di
R
= − dt
i
L
di
R
=
−
dt
∫i
L∫
R
ln i = − t + K
L
Para que a solução seja válida para t ≥ 0, a constante K deve ser escolhida tal
que a condição inicial de i(0) = I0 seja satisfeita, Portanto, em t = 0, temos:
ln i(0 ) = ln I 0 = K
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Substituindo o valor de K na solução, temos:
R
R
ln i = − t + K = − t + ln I 0
L
L
R
ln i − ln I 0 = − t
L
ln
i
R
=− t
I0
L
 R 
i(t ) = I 0 exp − t 
 L 
Esta é a corrente sobre R, portanto, a tensão é:
 R 
v(t ) = Ri(t ) = RI 0 exp − t 
 L 
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Solução 2: Assumir uma forma geral de solução baseada na inspeção da
equação a ser resolvida:
di R
+ i=0
dt L
Vamos incluir várias constantes desconhecidas e determinar seus valores tal
que a solução assumida satisfaça a equação diferencial e as condições iniciais
do circuito.
A corrente i não muda a sua forma sendo derivada, isto é, di/dt é um múltiplo de
i, assim, a única função que satisfaz esta condição é uma exponencial em t:
i(t ) = A exp(st )
d
[A exp(st )] + R [ A exp(st )] = 0
dt
L
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
R

 s +  A exp(st ) = 0
L

Assim, a solução i(t ) = A exp(st ) só é válida se A exp(st ) = 0 ou se s +
1º caso: faz i(t) = 0 para todo t, entretanto, i(0) = I0.
2º caso: s = −
R
, logo
L
 R 
i(t ) = A exp − t 
 L 
Fazendo i(0) = I0, pode-se obter A: i(0 ) = I 0 = A
A solução então fica:
 R 
i(t ) = I 0 exp − t 
 L 
R
=0
L
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
A constante de tempo é então:
τ=
L
R
[H/Ω] = [(V ⋅ s/A )/ (V/A )] = [s]
i(t)
I0
0,368I0
τ
t
Aumentando L aumenta-se τ, entretanto aumentando R diminui-se τ.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Potência instantânea entregue ao resistor:
 2R 
p(t ) = Ri 2 (t ) = RI 02 exp −
t
 L 
Energia absorvida pelo resistor para t → ∞ é:
∞
0
w(∞ ) = ∫ p(t )dt
∞
 2R 
= ∫ RI 02 exp −
t dt
0
 L 
 2R 
= − 1 LI 02 exp −
t
2

= 1 LI 02
2
∞
L 0
energia armazenada no circuito
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Cálculo da tensão v no indutor, aplicando-se a lei de Kirchhoff de correntes,
obtemos:
v 1 t
+
vdt + i (0 ) = 0
R L ∫0
i(t)
Derivando em t:
+
1 dv 1
+ v=0
R dt L
v(t)
dv R
+ v=0
dt L
Pode ser resolvida usando um dos métodos anteriores.
−
L
R
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Corrente i(t) e tensão v(t) no circuito RL. Circuito em regime
permanente cc imediatamente antes da abertura da chave.
t=0
i(t)
10 H
150 Ω
100 V
75 Ω
50 Ω
+
−
v(t)
Em t = 0−, chave fechada ⇒ indutor é um curto-circuito.
t = 0−
i(0-)
100 V
150 Ω
75 Ω
50 Ω
( )
i 0− =
100
= 2 [A ]
50
+
v(0−)
−
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Para t > 0, temos:
t>0
10 H
i(t)
100 V
150 Ω
75 Ω
50 Ω
+
−
v(t)
( ) ( )
i 0+ = i 0− = 2 [A ]
i(t)
+
10 H
v(t)
Req1
50 Ω
−
Req1 =
75 ⋅150
= 50 [Ω]
75 + 150
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Req = 50 + 50 = 100 [Ω]
i(t)
10 H
50 Ω
50 Ω
Constante de tempo:
τ=
L
10
=
= 0,1 [s ]
Req 100
Como I0 = i(0+) = 2 A, temos
i(t ) = 2 exp(− 10t ) [A ]
A tensão v(t) é dada por:
v(t ) = 10
di(t )
+ 50i
dt
= −100 exp(− 10t ) [V ]
+
−
v(t)
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Circuito com fonte de tensão dependente.
i(t)
L
R
L
+
−
ki(t)
di  R + k 
+
i = 0
dt  L 
di
+ Ri + ki = 0
dt
Resolvendo, obtemos:
 R+k 
i(t ) = I 0 exp −
t
L 

Constante de tempo:
τ=
L
R+k
A fonte dependente se comporta como um resistor de k Ω.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
8.4 Resposta a uma Função Excitação Constante
Circuitos que além de uma energia inicial armazenada, são excitados por fontes
independentes e constantes de tensão ou de corrente (funções de excitação).
Resposta deste circuitos consiste de duas partes, onde uma delas é sempre
uma constante.
t=0
ic
iR
I0
Capacitor: v(0−) = V0
+
R
C
−
v
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Para t > 0, a chave é fechada:
t = 0+
ic
iR
+
I0
R
C
−
v
Capacitor: v(0+) = v(0−) = V0
E a equação nodal no nó superior fica:
C
dv v
+ = I0
dt R
dv
1
I
+
v= 0
dt RC
C
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
dv
1
I
+
v= 0
dt RC
C
Resolvendo pelo método de separação de variáveis:
dv
v − RI 0
=−
dt
RC

dt 
 ×

 v − RI 0 
1
1
dv = −
dt
v − RI 0
RC
∫
1
1
dv = −
dt
v − RI 0
RC
ln(v − RI 0 ) = −
∫
t
+K
RC
 t

v − RI 0 = exp −
+ K
 RC

 t 
v = A exp −
 + RI 0
RC


Determinada pelas
condições iniciais do
circuito
A = exp( K )
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
A solução geral
 t 
v = A exp −
 + RI 0
RC


possui duas partes:
•
uma função exponencial idêntica a da resposta natural de
circuitos RC sem fontes (resposta natural vn).
•
uma função constante, dada por RI0, devida integralmente
à função de excitação (resposta forçada vf).
Com o passar do tempo a resposta natural desaparece e a solução fica
simplesmente RI0.
resposta natural vn ⇒ resposta homogênea vh
resposta forçada vf ⇒ resposta particular vp
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Constante A:
Valor de A deve ser escolhido de forma a satisfazer a condição de tensão inicial.
( ) ( )
Em t = 0+: v 0+ = v 0− = V0
 t 
Portanto, em t = 0+, v = A exp −
 + RI 0
 RC 
V0 = A + RI 0
requer que
A = V0 − RI 0
substituindo na solução temos
 t 
v = (V0 − RI 0 ) exp −
 + RI 0
RC


EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Resposta natural vn para V0 – RI0 > 0 e a resposta forçada vf:
vf
RI0
V0 – RI0
vn
t
Resposta completa v:
V0
v= vf + vn
RI0
t
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Corrente no capacitor para t > 0:
t = 0+
ic = C
dv
V − RI 0
 t 
=− 0
exp −

dt
R
 RC 
ic
iR
+
I0
R
C
Corrente no resistor para t > 0:
−
v
V − RI 0
 t 
iR = I 0 − ic = I 0 + 0
exp −

R
RC


Tensão no resistor muda abruptamente de RI0 em t = 0− para V0 em t = 0+.
Tensão no capacitor é contínua.
Resposta transitória:
porção da resposta completa que tende a
zero com o aumento do tempo.
Resposta em regime permanente: porção da resposta completa que permanece
após a resposta transitória ter se anulado.
EA-513 – Circuitos Elétricos I
No exemplo:
DECOM-FEEC-UNICAMP
resposta transitória = resposta natural
resposta em regime permanente = resposta forçada
Valores cc que constituem a condição e o estado permanente cc: v = RI0, ic = 0
e iR = I0
ic
iR
+
I0
R
C
−
v
Não se deve concluir, entretanto, que as respostas natural e forçada serão
sempre iguais às respostas transitória e em regime permanente,
respectivamente.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
8.5 Caso Geral
dy
+ Py = Q
dt
Expressão geral:
y = variável e P e Q = constantes
Solução pelo método do fator de integração, que consiste em multiplicar a
equação por um fator que torna seu lado esquerdo uma derivada perfeita e
então integrar ambos os lados.
Derivada de um produto:
( )
d
dy
ye Pt = e Pt + Pye Pt
dt
dt
 dy

=  + Py e Pt
 dt

fazendo
dy
+ Py = Q
dt
(× ePt )
 dy
 Pt
Pt
 + Py e = Qe
 dt

( )
d
ye Pt = Qe Pt
dt
integrar ambos os lados
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
( )
d
Pt
Pt
ye
dt
=
Qe
dt
∫ dt
∫
∫
ye Pt = Qe Pt dt + A
e− Pt
y = e− Pt Qe Pt dt + Ae− Pt
∫
Q Pt
e
P
No caso de cc onde Q é uma constante, temos:
y = Ae− Pt +
onde
Q
P
yn = Ae− Pt
yf =
Q
P
Note que 1/P é a constante
y = yn + y f
de tempo da resposta natural
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Calcular i2 para t > 0, dado que i2(0) = 1 A:
8Ω
4Ω
10 V
+
−
4Ω
i1
8i1 − 4i2 = 10
i2
di
− 4i1 + 12i2 + 1 2 = 0
dt
di2
+ 10i2 = 5
dt
dy
+ Py = Q
dt
P = 10, Q = 5, logo i2 = Ae−10t +
1H
y = Ae− Pt +
1
1
para i2(0) = 1, temos 1 = Ae−10⋅0 +
2
2
1
1
portanto, A = 1/2. Assim, a solução é dada por: i2 = e −10t +
2
2
Q
P
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
− Pt
+
Também pode-se obter y = Ae
Q
= yn + y f para o caso de Q = constante,
P
através da observação de
dy
+ Py = Q
dt
y = e− Pt Qe Pt dt + Ae− Pt
∫
A resposta natural satisfaz
dy
+ Py = 0
dt
que resulta em s + P = 0
yn = Ae st
s = −P
yn = Ae− Pt
Resposta forçada:
yf = K
Q
dy
y
=
K
=
+ Py = Q resulta em 0 + PK = Q ou f
que substituindo em
P
dt
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
8.6 Procedimento Simplificado
Obtenção dos valores de correntes e tensões de circuitos, sem fontes
dependentes, pela formulação da solução através de inspeção do circuito.
Exemplo: i2(0) = 1 [A]
8Ω
4Ω
10 V
+
−
i1
4Ω
i2
1H
sabemos que: i2 = i2n + i2f
i2n = resposta natural = mesma forma que a resposta sem fontes.
i2f = resposta forçada = constante.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Resposta natural: i2n
Pode-se ver a rede sem função excitação (fonte de 10 V é curto-circuitada):
8Ω
4Ω
i2n
4Ω
i2n
10 Ω
1H
1H
i2n = A exp(− 10t )
Resposta forçada: i2f
Olhando o circuito quando i2n = 0, nesta hora o indutor é um curto, onde
8Ω
4Ω
10 V
Portanto,
+
−
4Ω
i2f
i2 = i2n + i2 f = A exp(− 10t ) +
i2 f =
1
2
1
2
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
A constante A é determinada a partir da condição inicial i2(0) = 1:
1 = Ae−10⋅0 +
1
2
portanto, A = 1/2. Assim, a solução é dada por:
1
1
i2 = exp(− 10t ) +
2
2
Obs.: O cálculo de A deve ser feito sempre aplicando a condição inicial à
resposta completa.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Cálculo de i para t > 0, dado que v(0) = 24 V
6Ω
i
1A
4Ω
0,02 F
+
−
v
i = in + if
in possui a mesma forma de vn, a resposta natural da tensão sobre o capacitor.
A resposta natural de cada corrente ou tensão no circuito tem a mesma forma
de vn, uma vez que nenhuma operação (adição, subtração, diferenciação ou
integração) altera a natureza da exponencial exp(-t/τ).
Constante de tempo no capacitor: τ = 0,2 s, portanto in = A exp(− 5t )
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Regime permanente ⇒ capacitor = circuito aberto
6Ω
resposta forçada, por inspeção:
i f = 1 [A ]
Portanto,
if
4Ω
1A
i(t ) = A exp(− 5t ) + 1
1-i(0+)
Para avaliar o valor de A, precisamos encontrar i(0+).
Para t = 0+, temos v(0) = v(0+) = 24 V
Somando as tensões ao redor da malha direita, temos:
( ) [ ( )]
− 4i 0+ + 6 1 − i 0+ + 24 = 0
( )
i 0+ = 3
i(0+) 6 Ω
1A
4Ω
v(0+)
+
−
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Substituindo esta corrente inicial na solução i(t ) = A exp(− 5t ) + 1 , temos:
3 = A +1
Portanto, A = 2 e
i = 1 + 2 exp(− 5t )
[A]
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Determinar i e v.
15 Ω
10 Ω
i
30 Ω
1H
v
t=0
+
0,15 F
−
20 Ω
6A
Circuito em regime permanente cc em t = 0− com a chave aberta.
Indutor = curto ⇒ iindutor = i15Ω = i
15 Ω
Capacitor = aberto ⇒ v = v20Ω
10 Ω
i
+
30 Ω
v
−
20 Ω
6A
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Por divisão de corrente,
15 Ω
10 Ω
i
i10Ω
+
30 Ω
i20Ω
v
−
Req = 10 +
i10Ω = 6 ⋅
20
= 3 [A ]
20 + 20
Portanto, i = 2 A e i20Ω = 3 A
15 ⋅ 30
= 20 Ω
15 + 30
i = 3⋅
30
= 2 [A ]
15 + 30
v = 20 × 3 = 60 V
20 Ω
6A
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Então, i(0−) = 2 A e v(0−) = 60 V
Quando a chave é fechada em t = 0, temos:
15 Ω
10 Ω
i
30 Ω
1H
t=0
v
+
−
0,15 F
20 Ω
Rede RL sem fontes:
Rede RC excitada com:
i(0+) = i(0-) = 2 A.
v(0+) = v(0−) = 60 V
i = 2 exp(− 15t )
[A]
v = 40 + 20 exp(− t )
[V]
6A
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
8.7 Função Degrau Unitário
Funções singulares: funções
de
excitação
que
mudam
seus
abruptamente.
Função degrau unitário:
0
u (t ) = 
1
t<0
t>0
u(t)
1
0
t
valores
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Fonte de degrau de tensão de V volts:
t=0
Vu(t)
+
−
+
V
Vu(t)
−
Fonte degrau de corrente de I ampères:
t=0
Iu(t)
I
Iu(t)
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Generalização da função degrau unitário para t = t0:
0
u (t − t0 ) = 
1
t < t0
t > t0
u(t – t0)
1
0
t0
t
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Pulso retangular
v1(t)
V
0
t0
xt)
V
t t
0
y(t)
t0
0
-V
t
0

v1(t ) = V

0
t
t<0
0 < t < t0
t > t0
v1(t ) = V [u (t ) − u (t − t0 )]
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Trem de pulsos retangulares
v2(t)
V
0
t0
v2 (t ) = V
T
∞
T + t0
2T
2T + t0
3T
3T + t0
∑ [u (t − nT ) − u(t − nT − t0 )]
n =0
t
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
8.8 Resposta ao Degrau
É a resposta de um circuito tendo somente uma entrada, que é a função degrau
unitário (tensão ou corrente).
Não existem energias iniciais presentes nos elementos do circuito.
Todas as tensões ou correntes no circuito são zero em t = 0−.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Resposta v ao degrau no circuito RC.
R
vg = u(t)
+
−
C
Aplicando Lei de Kirchhoff de correntes:
C
dv v − v g
+
=0
dt
R
dv v − u (t )
+
=0
dt
RC
dv
v
1
+
=
u (t )
dt RC RC
+
−
v
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Para t < 0, temos u(t) = 0, logo
 t 
v = A exp −

 RC 
dv
v
+
=0
dt RC
Aplicando a condição inicial v(0−) = 0, obtemos A = 0 e portanto v(t ) = 0
Para t > 0, temos u(t) = 1, logo
dv
v
1
+
=
u (t )
dt RC RC
dv
v
1
+
=
dt RC RC
v = vn + v f
 t 
vn = A exp −

RC


vf =1
 t 
v = A exp −
 +1
RC


EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Aplicando a condição inicial v(0+) = v(0−) = 0, obtemos A = −1 e portanto
para t > 0, temos:
 t 
v(t ) = 1 − exp −

 RC 
Para todo t, temos:
0

v(t ) = 
 t 
1
exp
−
−


RC



t<0
t >0

 t 
v(t ) = 1 − exp −
u (t )
 RC 

t=0
Circuito equivalente, com v(0−) = 0 para t < 0: 1 V
R
C
+
−
v
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Resposta v2 ao degrau no circuito RC + op-amp.
C
i
+
R
−
+
+
v1
v2
–
–
v
dv
Equação nodal: 1 + C 2 = 0
R
dt
dv2
1
=−
v1
dt
RC
v2(t) é proporcional à integral de v1(t) se v2(0+) = 0: v2 = −
v2 = −
( )
1 t
v1dt + v2 0+
∫
RC 0
1 t
v1dt
∫
0
RC
Circuito integrador.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Seja v1 = Vu(t), então v2(0+) = v2(0−) = 0, Portanto,
v2 (t ) = − V
t
u (t )dt
RC ∫0 +
Se t < 0, então u(t) = 0 e v2(t) = 0.
Para t > 0, então u(t) = 1 e v2 (t ) = − V t u (t )
função rampa
RC
v2
t
V
RC
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Cálculo da tensão v(t), dado que i(0−) = 0 e que a função de
excitação é ig (t ) = 10[u (t ) − u (t − 1)]
[A]
ig(t)
10
1
0
t
i
5H
ig(t)
3Ω
+
2Ω
v(t)
−
No instante t = 1 s, ig(t) torna-se zero e a resposta é simplesmente a resposta
sem fontes.
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Solução do problema envolve o cálculo da resposta do circuito ao degrau
para t < 1 [s] para, em seguida, calcular a resposta sem fontes para t > 1 [s].
ig(t)
10
Resposta ao degrau é da forma: v = vn + v f
 Req 
 5 
vn = A exp −
t  = A exp − t  = A exp(− t )
 5 
 L 
0
1
i
t
5H
3Ω
ig(t)
+
2Ω
v(t)
−
 3 ⋅ 10 
v f = 2
= 12

 2 + 3
(por divisão de corrente e lei de Ohm)
v = A exp(− t ) + 12
Como i(0+) = i(0−) = 0, então v(0+) = v(0−) = 0
0
v=
12[1 − exp(− t )]
A = −12
t<0
0 < t <1
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
ig(t)
Para t > 1, temos:
10
v = B exp(− t )
Em t = 1−, temos:
0
t
1
i
( )
v 1− = 12[1 − exp(− 1)]
5H
3Ω
como a corrente no indutor é contínua, v(1−) = v(1+).
( )
Solução para t > 1:
12[1 − exp(− 1)]
= 12[1 − exp(− 1)]exp(1)
exp(− 1)
v = 12[1 − exp(− 1)]exp[− (t − 1)]
2Ω
v(t)
−
v 1+ = B exp(− 1) = 12[1 − exp(− 1)]
B=
+
t >1
Solução para todo t :
v = 12[1 − exp(− t )][u(t ) − u(t −1)] +12[1 − exp(−1)]exp[− (t −1)]u(t −1)
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
ig(t)
10
0
v(t)
1
t
12[1 − exp(− t )]
12
12[1 − exp(−1)]exp[− (t − 1)]
7,59
0
1
2
3
t
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
8.9 Aplicação da Superposição
Aplicação da superposição para a obtenção de soluções de circuitos RC e RL.
Exemplo:
i
5H
ig(t)
3Ω
+
2Ω
v(t)
−
ig = 10u (t ) − 10u (t − 1)
i1 = 10u (t )
i2 = −10u (t − 1)
ig = i1 + i2
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
i
5H
i1
i2
3Ω
+
2Ω
v(t)
−
Pelo princípio de superposição, temos como saída: v = v1 + v2
Resposta devida ao degrau de corrente i1: v1 = 12 [1 − exp(− t )]u (t )
Resposta devida ao degrau de corrente i2: i2 é o negativo de i1 atrasado de 1 s,
isto é,
Solução geral:
v2 = −12 [1 − exp[− (t − 1)] ]u (t − 1)
v = 12[1 − exp(− t )]u(t ) − 12[1 − exp[− (t − 1)] ]u(t − 1)
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Exemplo: Circuito com duas fontes independentes, tensão inicial sobre o
capacitor v(0) = V0.
i
+
R1
V1
+
−
v −
C
R2
i
I1
Aplicando Lei de Kirchhoff de tensões na malha esquerda:
(R1 + R2 ) i + 1 ∫0t idt + V0 = V1 − R2 I1
C
(×K)
t
(R1 + R2 )(Ki ) + 1 ∫ (Ki )dt + KV0 = KV1 − R2 (KI1 )
C 0
Note que a resposta de corrente torna-se Ki quando as fontes e a tensão inicial
do capacitor são multiplicadas por K (propriedade da proporcionalidade)
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Empregando o princípio da sobreposição para a determinação de v:
Tensão sobre o capacitor devida somente à fonte de tensão:
v1
−
+
R1
V1
C
+
−
R2
Tensão inicial sobre o capacitor v1(0) = 0, então



t

v1 = V1 1 − exp −
 ( R1 + R2 )C 

EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Tensão sobre o capacitor devida somente à fonte de corrente:
+
R1
v2
−
C
R2
Tensão inicial sobre o capacitor v2(0) = 0, então



t

v2 = − R2 I1 1 − exp −
(
)
R
+
R
C

1
2 

I1
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Tensão sobre o capacitor sem a presença das fontes:
v3
−
+
R1
C
R2
Tensão inicial sobre o capacitor v3(0) = V0, então


t

v3 = V0 exp −
(
)
 R1 + R2 C 
EA-513 – Circuitos Elétricos I
Resposta completa:
DECOM-FEEC-UNICAMP
v = v1 + v2 + v3








t
t
t






v = V1 1 − exp −
−
R
I
1
−
exp
−
+
V
exp
−
2 1

 0




 ( R1 + R2 )C 
 ( R1 + R2 )C 
 ( R1 + R2 )C 




t

v = V1 − R2 I1 − (V1 − R2 I1 − V0 ) exp −
 ( R1 + R2 )C 
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Outra solução:
Por inspeção verifica-se que a solução consiste de uma resposta forçada vf e
uma resposta natural vn :
vf = vf1 + vf 2
Superposição para encontrar vf:
+
R1
V1
+
−
v1
−
aberto
+
R1
C
v2
−
aberto
C
R2
R2
v f 2 = − R2 I1
v f 1 = V1
v f = V1 − R2 I1
I1
EA-513 – Circuitos Elétricos I
DECOM-FEEC-UNICAMP
Resposta natural vn :
+
R1
v3
−
C
R2


t

vn = A exp −
 (R1 + R2 )C 
Resposta total:


t

v = V1 − R2 I1 + A exp −
 (R1 + R2 )C 
Como v(0) = V0, temos
V0 = V1 − R2 I1 + A
Então,
⇒
A = R2 I1 − V1 + V0


t

v = V1 − R2 I1 + (R2 I1 − V1 + V0 ) exp −
 (R1 + R2 )C 