Limite - PauloFernando

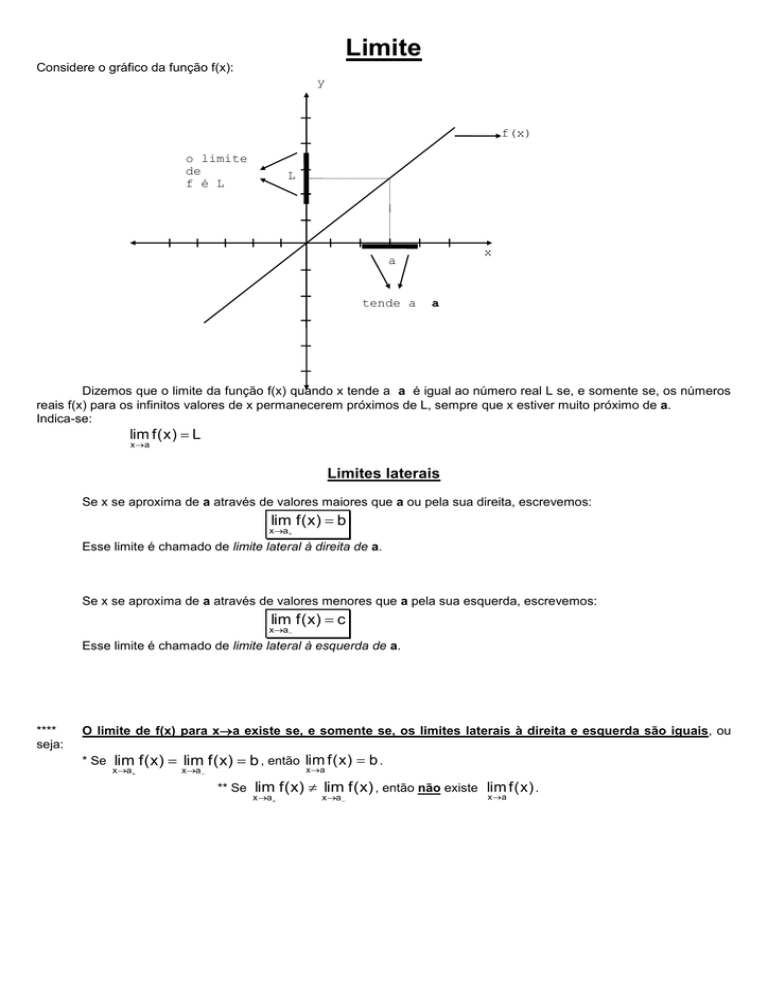
Limite
Considere o gráfico da função f(x):
y
f(x)
o limite
de
f é L
L
x
a
tende a
a
Dizemos que o limite da função f(x) quando x tende a a é igual ao número real L se, e somente se, os números
reais f(x) para os infinitos valores de x permanecerem próximos de L, sempre que x estiver muito próximo de a.
Indica-se:
lim f ( x )  L
x a
Limites laterais
Se x se aproxima de a através de valores maiores que a ou pela sua direita, escrevemos:
lim f ( x)  b
xa
Esse limite é chamado de limite lateral à direita de a.
Se x se aproxima de a através de valores menores que a pela sua esquerda, escrevemos:
lim f ( x)  c
xa
Esse limite é chamado de limite lateral à esquerda de a.
****
seja:
O limite de f(x) para xa existe se, e somente se, os limites laterais à direita e esquerda são iguais, ou
* Se
lim f ( x)  lim f ( x)  b , então lim f ( x )  b .
x a
x a
x a
** Se
lim f ( x)  lim f ( x) , então não existe lim f ( x ) .
xa
xa
xa
Exemplos:
1) Observe o gráfico da função f(x):
4
2
1
 lim f ( x )  4
x1

f ( x)  2
xlim
1
2) Sendo f(x) =
logo, não existe lim f ( x )
x1
x 2  4x, x  1
, então

6
x

1
,
x

1

lim f ( x )  lim ( x 2  4 x )  5
x 1
x 1
lim f ( x )  lim (6 x  1)  5
x 1
logo lim f ( x )  5
,
x 1
x 1
Teoremas sobre Limites
Limite de uma constante
O limite de uma constante é a própria constante, isto é:
lim k  k
x a
2 2

x  8 3
3
Exemplos: a) lim 3  3
b) lim
x4
Limite da soma ( ou da diferença )
O limite da soma (ou da diferença) de duas funções é igual à soma ( ou à diferença ) dos limites dessas funções,
isto é:
limf ( x )  g( x )  lim f ( x )  lim g( x )
x a
x a
Exemplos:
a)
lim( x 2  3)  lim x 2  lim 3  16  3  19
x 4
x 4
x 4
b) lim( x  5)  lim x  lim 5  2  5  3
x 2
x 2
x 2
x a
Limite do produto
O limite do produto de duas funções é igual ao produto dos limites dessas funções, isto é:
lim f ( x )  g( x )  lim f ( x )  lim g( x )
x a
Exemplo: lim 4x
x 2
2
x a
x a
 lim 4  lim x 2  4  4  16
x 2
x 2
Limite do quociente
O limite do quociente de duas funções é o quociente dos limites dessas funções (exceto quando o limite do
divisor for igual a zero), isto é:
f (x)
f ( x ) lim
 x a
x a g( x )
lim g( x )
lim
x a
( x  3) 5
x  3 lim
 x 2

x 2 x  2
lim( x  2) 4
Exemplo: lim
x 2
Limite de uma potência
O limite de uma potência enésima de uma função é igual à potência enésima do limite dessa função, isto é:


lim[f ( x )]n  lim f ( x )
x a
Exemplo:

x a
n

lim5x   lim 5x  10 2  100
2
x 2
2
x 2
Limite de uma raiz
O limite da raiz enésima de uma função é igual à raiz enésima do limite dessa função, isto é:
lim n f ( x )  n lim f ( x )
x a
Exemplo:
x a
lim 5 2x 4  5 lim 2x 4  5 32  2
x 2
x 2
Limites infinitos e limites para x tendendo ao infinito
Ampliaremos agora o conceito de limite, introduzindo o elemento infinito, que representamos por .
O símbolo  não representa um número, portanto, não se efetuam com ele as operações que realizamos com os
números reais.
Exemplo:
Seja o gráfico da função f(x) =
1
.
x
10
8
6
4
2
0
-5
-4
-3
-2
-1
0
1
2
3
4
5
-2
-4
-6
-8
-10
Quando x se aproxima de zero, pela direita, y cresce indefinidamente superando qualquer valor arbitrário que
fixemos, isto é, y tende a mais infinito e indicamos:
lim
x 0 
1
 
x
Quando x se aproxima de zero, pela esquerda, y decresce indefinidamente, isto é, y tende a menos infinito e
indicamos:
lim
x 0 
Observe que não existe lim
x 0
1
 
x
1
porque os limites laterais são diferentes.
x
A partir do mesmo gráfico, podemos concluir que:
* quando x cresce indefinidamente, o gráfico quase encosta no eixo x, isto é, y tende a zero:
1
0
x   x
lim
* quando x decresce indefinidamente, o gráfico quase encosta no eixo x, isto é, y tende a zero:
1
0
x   x
lim
Técnica para cálculo de limites
1º caso
A função existe, isto é, está definida no ponto considerado.
Técnica de resolução: Substituição direta do valor de x.
x4 34
1


x 3 x  1
 3 1
4
Exemplo: lim
2º caso
A função polinomial não tem denominador e x tende a + ou .
Técnica de resolução: Colocar em evidência a maior potência de x.
Exemplo:
3º caso
 
2 1
1
1
lim 3x 4  2x 3  x 2  x  1  lim  x 4  3   2  3  4
x 
x x
x
x
 
x 



4
  lim 3x  
x 

O numerador se aproxima de um número real não-nulo e o denominador tende a zero.
Técnica de resolução: Se o denominador tende a zero, a fração cresce ou decresce indefinidamente e o limite será + ou
.
Exemplos: a) lim
x 1
3x
 
x2 1
Para sabermos o sinal da resposta com x tendendo a 1 pela direita, podemos fazer x=1,1 e verificar qual é o sinal
da função.
f(x) =
3x
3  1,1

0
2
x  1 1,12  1
Se a função é positiva para x =1,1, o limite tende a +.
b) lim
x 1
3x
 
x2 1
Fazendo x = 0,9, temos:
f(x) =
3  0,9
0,92  1
 0 , logo, o limite tende a .
4º caso
O numerador tende a um número real e o denominador se aproxima de + ou .
Técnica de resolução: Neste caso o limite é sempre igual a zero.
Exemplos:
a) lim
x 
7
0
x
3
0
x   x 3  1
b) lim
5º caso
O numerador e o denominador tendem a + ou .
Técnica de resolução: Divida o numerado e o denominador pela maior potência de x e faça a substituição.
Exemplos:
a)
x 5 2x 2
x
3
 7  7  7
7
x  2x  x  3
x 
lim
 lim x 7 x 3 x
7
3
x 
x


x  4x  1
x
4x
1
 7  7
7
x
x
x
1
2
1
3
 5  6  7
2
x
x
x
x  0 0
 lim
x 
4
1
1
1 4  7
x
x
5
2
b)
1
1 4
x5  x
x  
lim
 lim
x   x 2  2x
x   1
2
 4
3
x
x
6º caso
O numerador e o denominador tendem a zero.
Técnica de resolução: Devemos fatorar o numerador e o denominador e simplificar a função ou multiplicar e dividir a
fração pelo conjugado do numerador ( denominador ).
Exemplos:
a)
x 2  2x
x( x  2)
 lim
 lim x  2
x 2 x  2
x 2 x  2
x 2
lim
b)
lim
x 0
1 x  1
 lim
x 0
x
 lim
x 0
1 x  1


x 1 x  1
 1 x  1 1 x  1 
x  1  x  1
 lim
x 0
1
 1 x  1

1
2
Limite exponencial fundamental
x
1

Seja a função f(x) = 1   , definida num domínio D.

x
Tabelando a função f, temos
X
1
2
3
5
10
100
1000
10000
.
.
.

y
2,000
2,250
2,369
2,489
2,594
2,705
2,717
2,718
.
.
.
e
Para os valores de x correspondem valores de y que vão se aproximando do número irracional e, chamado número de
Euler (Leonhard Euler 1707-1783).
x
x
1
1


lim 1    lim 1    e
x 
x  
x
x


Onde e = 2,71828182... ( usando oito casas decimais )
4x
1

1º Exemplo: Calcular lim 1   .
x 
x

 1
Resolução: lim 1  
x 
 x
4x
4
4
 1  x 
  1 x 
 lim 1      lim 1     e 4
x 
 x  
x x  
Resposta: e4
x
x  6
2º exemplo: Calcular lim 
 .
x 
 x 
x
x  6
lim 
 = lim 

x   x
x  x

x
Resolução:
Fazendo
x

6
 6
  lim 1  
x 
x
x

x
6 1
  x  6y
x y
Se x   y 
Substituindo, temos:
x

 6
lim 1    lim 1 
x 
y 
 x

1

y 
6y
 
  lim 1 
y
6
y
1 
   e6
y  

Resposta: e6
Limite trigonométrico fundamental
sen x
1
x 0
x
lim
Ou, podemos demonstrar que, de modo generalizado, temos:
lim
x 0
1º exemplo:
Calcular lim
x 0
sen kx k

mx
m
sen 8 x
.
3x
Logo, usando a expressão generalizada, temos:
sen 8 x 8
lim
= .
x 0
3
3x
Resposta:
8
3
2º exemplo:
Resposta:
sen 5 x
.
x0 sen 4 x
sen 5x
5
sen 5x
5x  5  1  5
lim
 lim
x 0 sen 4 x
x 0
sen 4x 4  1 4
4
4x
Determinar lim
5
4
Função contínua
Uma função f(x) definida em um intervalo J, com a  J, é dita contínua em x = a, se: lim f ( x )  f (a)
x a
1º exemplo: Verificar se a função f(x) =
Resolução:
Cálculo de f(3): f(3) =
x2  4
é contínua em x =3.
x2
32  4
=5
32
x2  4
( x  2)( x  2)
Cálculo de lim f(x): lim
 lim
 lim( x  2)  5
x 3 x  2
x 3
x 3
( x  2)
Logo, f(x) é contínua em x=3.
Observe que f(x) não é contínua em x=2, pois, não existe f(2).
2º exemplo: Verificar se a função f(x) =
x7
é contínua em x=1.
x 1
Resolução: Como não existe f(1), porque teríamos uma divisão por zero, a função é descontínua em x=1.
3º exemplo: Determinar m  R de modo que f(x) =
x 2  5x  4, se x  4
seja contínua em x = 4.

, se x = 4
3m
Resolução: Cálculo do limite de f(x):
lim f ( x)  lim( x 2  5x  4)  4 2  5  4  6  2
x 4
x 4
Para que a função seja contínua em x = 4, devemos ter:
lim f ( x )  f ( 4)  2  3m  m 
x 4
Resposta: m =
2
.
3
2
.
3