(a) Encontre o domínio e contradomínio de f. Domf = R\{2} - DMA-UEM

Centro de Ciências Exatas - Departamento de Matemática
1a.Avaliação de Aprendizagem - 22/03/2012 - Cálculo - 3203 - Turmas 31 e 32
R.A.:
NOME:
1. Considere a função f(x) =
2x−5
(x−2)
(a) Encontre o domínio e contradomínio de f. Domf = R\{2} e CDomf = R.
(b) Encontre a imagem de f (sugestão: resolva a equação y =
2x−5
(x−2) ).
Im f = R\{2}
(c) Analise o sinal de f(x), ou seja, os valores onde f(x) é maior do que zero, igual a
zero e menor do que zero. f é maior do que zero em [ 52 , +∞[, f é menor do que
zero em ]2, 52 [, f é igual a zero em 52 .
(d) Encontre as assíntotas horizontais e verticais de f (x). x = 2 é assíntota vertical e
y = 2 é assíntota horizontal.
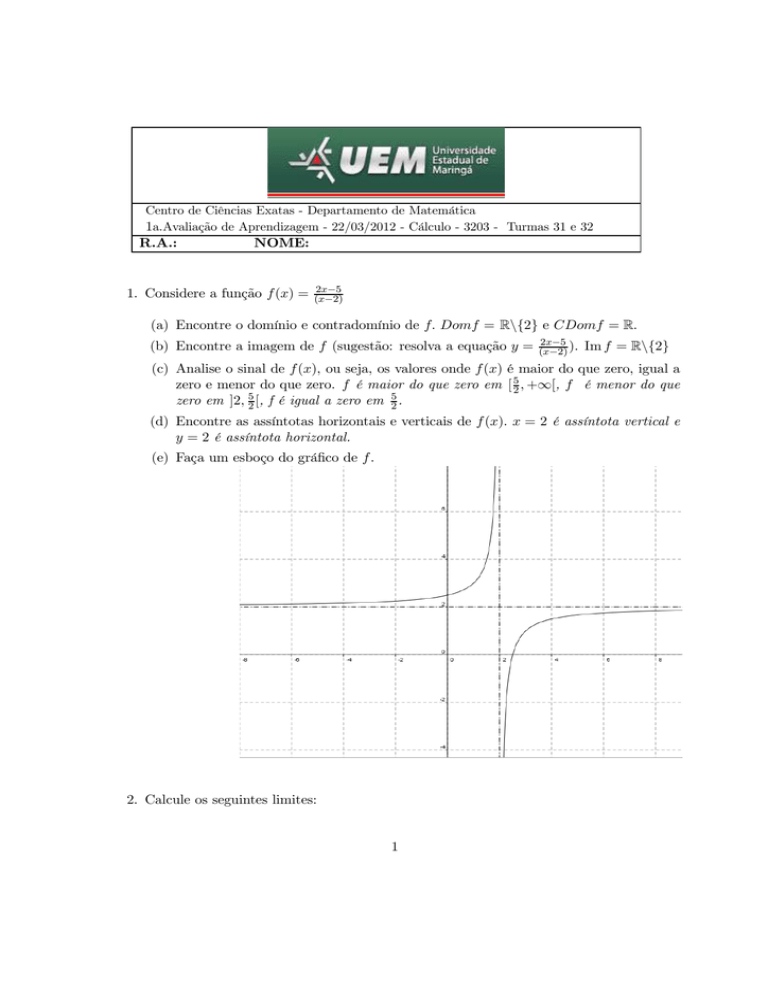
(e) Faça um esboço do gráfico de f.
2. Calcule os seguintes limites:
1
√
x+1−1
= 12
x
x→0
lim √x+1 = 1
x→+∞ x2 −5
(a) lim
(b)
sen(2x)
x→0 sen(3x)
(c) lim
=
2
3
3. Determinar o conjunto dos números reais para os quais é verdadeira a desigualdade
|2x − 3| ≤ |6 − x|, Justifique todos os passos utilizados.
A solução é [−3, 3].
4. Considere a função f cuja regra é dada por f(x) =
(x3 −2x2 +3x−6)
(x−2)
a
se x = 2
se x = 2.
(a) Determine o domínio, contradomínio e a imagem da funcão real .Domf = R, CDomf =
R e Im f = (R\{7}) ∪ {a}
(b) Analise a continuidade desta função e encontre o valor de a para que f seja contínua
em todo o seu domínio. f é contínua em todos os pontos exceto em x = 2, caso a
= 7. Se a = 7 temos que f é contínua em R.
(c) Construir um esboço do gráfico considerando o valor de a encontrado no item anterior.
2
Observações:
• A prova é individual.
• Todas as respostas deverão ser justificadas.
• Valor das questões: 2, 0 → 2, 5 → 2, 5 → 3, 0, na ordem crescente de porcentagem de
acerto.
BOA PROVA A TODOS!
3