CF12 - Reflexão e transmmissão numa interface entre dois meios

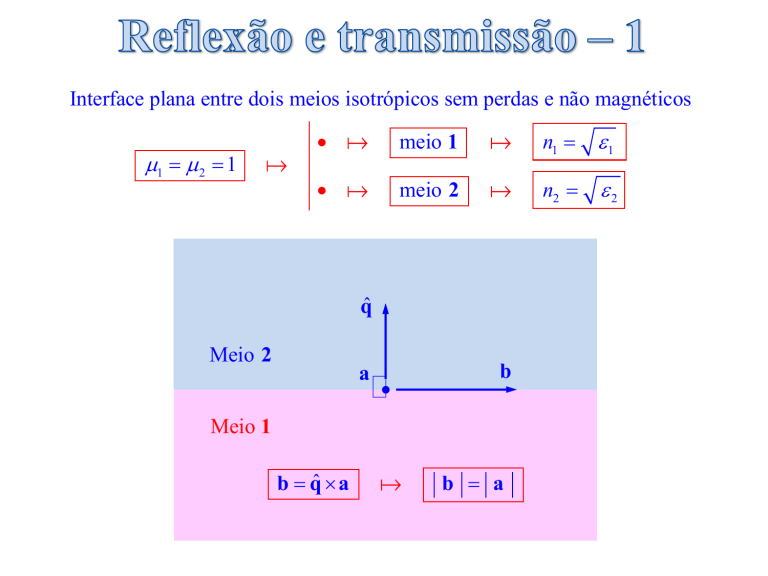
Interface plana entre dois meios isotrópicos sem perdas e não magnéticos
1  2  1

meio 1
n1 
1

meio 2
n2 
2
q̂
Meio 2
a

b
Meio 1
b  qˆ  a
b  a
Interface plana entre dois meios isotrópicos sem perdas e não magnéticos
1  2  1

meio 1
n1 
1

meio 2
n2 
2
Meio 2
kt
a  n1 k0 sin 1 
q̂
a  b
 q  n k cos  
1 0
1
 i
 qr   qi

2 2
2
 qt  n2 k0  a
ki
a
k n k
2
2 2
1 0
ki

k 2  n22 k02
b
kr
b  qˆ  a
Meio 1
k i  b  qi qˆ
k r  b  qr qˆ
k t  b  qt qˆ
 campo eléctrico reflectido
 campo eléctrico transmitido




 
E   B a  B  kˆ  a 
E   C a  C  kˆ  a 
i
E0   A a  A kˆ i  a
 campo eléctrico incidente
r
0

r
t
0

t
polarização perpendicular (ou TE ou ainda horizontal )
polarização paralela (ou TM ou ainda vertical )
 B    
B  0
  
0   A 
   A 
 C    0   A 
C   0   A 
 
  
matriz de
reflexão
matriz de
transmissão
 
Γ
 0
0
 
  0 
τ

0



Equações de Fresnel


 
 
n1 cos 1   n2 cos  2 
n1 cos 1   n2 cos  2 
n2 cos 1   n1 cos  2 
n2 cos 1   n1 cos  2 
Polarização
Ângulo de
paralela
Brewster
Reflexão
interna
n1  n2
1  2
CASO PARTICULAR


   1   
  1  
2 n1 cos 1 
n1 cos 1   n2 cos  2 
cos 1 
 cos    n
2
 0
Ângulo
crítico
Reflexão
n1  n2
interna
&
total
1   c
1
cos  2   n2 cos 1 
 n2 

n
 1
1   B  tan 1 
 n2 
1   c  sin  
 n1 
1
    1
2 n1 cos 1 
1   2 
2 

2

2
Equações de Fresnel  forma alternativa
1  2
CASO PARTICULAR
Lei de Snell
n1 sin 1   n2 sin  2 

Coeficientes
sin  2  1 
de reflexão
tan 1   2 

 

   1   

  1  
Coeficientes
de transmissão
 
sin  2  1 
tan 1   2 
2 sin  2  cos 1 
sin 1   2 
cos 1 
 cos  
2

2 sin  2  cos 1 
sin 1   2  cos 1   2 
Reflexão externa
n1  n2
Exemplo numérico
Polarização paralela  TM 
Polarização perpendicular  TE 
 1
  1


n2  1.5 n1
 B  56.31




1
B
Reflexão interna
n1  n2
Polarização paralela  TM 
Polarização perpendicular  TE 
  1
 1
 c  41.81




n1  1.5 n2
Exemplo numérico
c
c



1
 B  33.69
B
c
Generalização
CASO GERAL
1  2

meio 1
n1 
1 1
1 
1 1

1 n1

meio 2
n2 
 2 2
2 
2 2

 2 n2
1  2

 2 cos 1   1 cos  2 
 
 2 cos 1   1 cos  2 

 

   1   

  1  
1 cos 1    2 cos  2 
1 cos 1    2 cos  2 
2 2 cos 1 
1 cos  2    2 cos 1 
cos 1 
 cos  
2

2 2 cos 1 
1 cos 1    2 cos  2 
CASO GERAL
1  2






 «campo magnético» incidente
H 0  
1 
A kˆ i  a  A a 

0 1 
 «campo magnético» reflectido
H 0  
1 
B kˆ r  a  B a 

0 1 
 «campo magnético» transmitido
H 0  
i
r
t
CASO GERAL
Incidência normal
1
C kˆ t  a  C a 

0  2 
1  2
1   2  0
 2  1
 2  1

    

   1      1   
2 2
 2  1
CASO GERAL
 campo incidente
 campo reflectido
 campo transmitido
1  2



i
E0   A a  A kˆ i  a

H 0  

r
E0     A a   A kˆ r  a

H 0  

t
E0     A a   A kˆ t  a

H 0  
i


1 
A kˆ i  a  A a 

0 1 

r
t





1 
  A kˆ r  a   A a 

0 1 
1


  A kˆ t  a   A a 

0  2 
 campo eléctrico total no meio 1
E   E0  e

 campo eléctrico total no meio 2
E   E0  e
1
i
2
t
i  k i r 
i  k t r 
 E0  e
r
i  k r r 
 e i t

e i t
Exemplo
Campo eléctrico total no meio 1 (no domínio do tempo). Caso particular de incidência
normal 1   2  0, k r   k i  em que o meio 2 é um PEC  2  0,       1 .


r
i
i
Neste caso é E0    E0  . Para E0   R 3 , vem sucessivamente com   kˆ i  r  qˆ  r :
 

1
i
i qˆ r
 i qˆ r
E1  , t    E   E0   e    e    e  i  t




 E0    2 i sin  ki    cos  t   i sin  t  
i

 2 E0  sin  ki   sin  t  .
i
Obviamente que, no PEC  perfect electric conductor  em que   0, é sempre:
E1   0, t   0 .