Módulo e Argumento de um Número Complexo

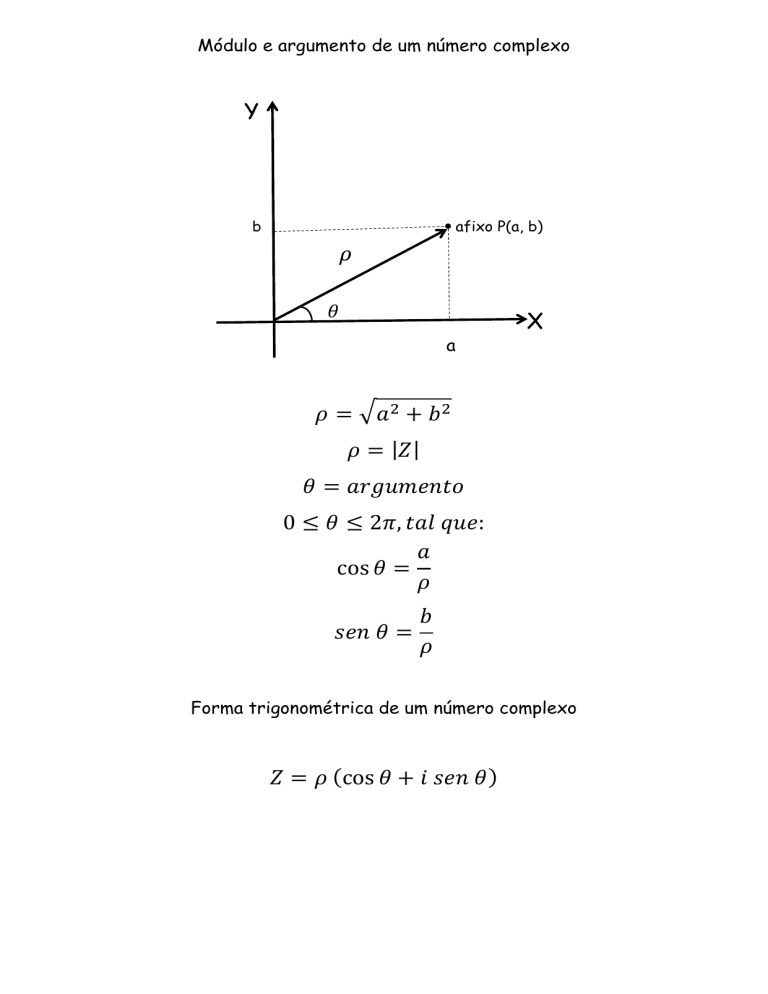
Módulo e argumento de um número complexo
b
afixo P(a, b)
𝜃
a
𝜌 = √𝑎 2 + 𝑏 2
𝜌 = |𝑍|
𝜃 = 𝑎𝑟𝑔𝑢𝑚𝑒𝑛𝑡𝑜
0 ≤ 𝜃 ≤ 2𝜋, 𝑡𝑎𝑙 𝑞𝑢𝑒:
𝑎
cos 𝜃 =
𝜌
𝑏
𝑠𝑒𝑛 𝜃 =
𝜌
Forma trigonométrica de um número complexo
𝑍 = 𝜌 (cos 𝜃 + 𝑖 𝑠𝑒𝑛 𝜃 )
EXERCÍCIOS:
1) Represente num mesmo gráfico os afixos dos seguintes números complexos:
Z1= 2 + 3i;
Z2= -3 + i;
Z3= -1 – 2i;
Z4= 3 – i;
Z5= 2i; Z6= 4
2) Os números complexos 2 + 3i, 4 – 3i, -4 + 3i e -2 - 3i, quando representados
graficamente, formam um
A) Retângulo
B) Paralelogramo
C) Quadrado
D) Losango
3) Considere o ponto P no plano de Argand-Gauss. O ponto P da figura é o afixo do
número complexo Z, resultado da operação
(A) (3+2i) − (5−2i)
(B) (3+2i) ∙ (5−2i)
(C) (3+2i) : (5−2i)
(D) (3+2i) + (5−2i)
4) Determine o módulo e represente graficamente os seguintes números complexos:
a) Z1= 3 – 4i b)Z2= -2 +2i
c)Z3= 8
d)Z4=-5i
e)Z5= (1 –i).(2 +3i)
5) Determine o argumento dos seguintes números complexos:
a) Z1= 2 + 2i
b) Z2= 1 - √3i
c)Z3= -8
d)Z4= 4i
e)Z5= 3i (1 - √3𝑖)
6) Escreva na forma trigonométrica os seguintes números complexos:
a) Z1= 1 + √3𝑖
b)Z2= −√2 + √2𝑖
c)Z3= -5i
d)Z4= 3
e)Z5= 2i (1 + i)
7) Escreva os seguintes números complexos na forma algébrica:
a) Z1= 6(cos 𝜋 + 𝑖 𝑠𝑒𝑛 𝜋)
b) Z2= 3√2(cos
𝜋
7𝜋
4
+ 𝑖 𝑠𝑒𝑛
𝜋
c) Z3=4(cos 3 + 𝑖 𝑠𝑒𝑛 3 )
d) Z4= 2√3(cos
5𝜋
3
+ 𝑖 𝑠𝑒𝑛
7𝜋
4
5𝜋
6
)
)
8) Considere a região do plano complexo indicada a seguir. Cada ponto da região é a
imagem de um complexo e foi objeto de uma transformação da figura pintada em
vermelho nas figuras a, b e c
Pode-se afirmar que a representação c) é resultado
(A) da soma com o número complexo 9+9i.
(B) do produto pelo número imaginário 2i.
(C) da soma ao número complexo 9i.
(D) do produto pelo número real 2.
9) O número complexo Z = (m2− 5m + 6) + (m2− 1) i, será um número imaginário puro para
(A) m = 0 ou m = 1
(B) m = 2 ou m = 3
(C) m = 5 ou m = − 6
(D) m = −1 ou m = 1
10) Dados números complexos: Z1= 8 + i e Z2= −7 − 2i; o resultado do cálculo de Z1 ∙ Z2 é
(A) –54 + 23i
(B) –54 – 23i
(C) 56 + 25i
(D) 56 – 25i