Lista de Exercícios

a)
Lista de Exercícios
2º ANO – Ensino Médio
1º BIMESTRE 2014
NOME:
TURMA:
2º
TURNO:
DATA:
Matutino
PROF:
/
/ 2014
NOTA:
Rennycky Cipriano
Lista de Exercícios
1A)
B)
C)
Resolva as seguintes equações em “i”:
x² - 2x + 5 = 0
x² - 6x + 10 = 0
– x² + 4x – 29 = 0
2a)
b)
c)
d)
e)
Encontre as potencias de i:
i 17
i 36
i 42
i 63
i30 + i31 ... + i60
3AB-
Efetue:
(2+i) + (4 – 2i) =
(7 – 3i) – (2 – 5i) =
4AB-
Sejam os números complexos z1= 7 – 5i, z2= - 3 + 4i e z3 = 2i. Determine:
Z1 – z2 + z3=
(z3 – z2) + (z2 – z1) =
5-
Efetue de (2 + 3i) . (4 – 5i) = e 𝒛 = 𝟐+𝟑𝒊
6complexos:
ABC7AB-
𝟒−𝟓𝒊
Determine no plano de Argand-Gauss o afixo de cada um dos seguintes números
Z1= 2 + 5i
Z1= - 3 – 2i
Z1= - 4 + 3i
Calcule o módulo de cada um dos seguintes complexos:
Z1= 2 + 3i
Z1= - 4 + 3i
b) 8-
Determine o argumento em cada um dos casos da questão 7.
9-
Os pontos (2, 5), (- 4, - 1) e (- 4, 5) são vértices de um triângulo, classifique-o.
10-
Encontre em cada caso a distância entre os pontos A(-2, 3) e B(- 6, 3)
11Calcule a área do triângulo cujos os pontos sobre o plano são A(2, -3) B(-3, 3) e C(1, 4)
encontre a medida de cada lado e classifique este triângulo quanto aos lados e ângulos.
12triângulo.
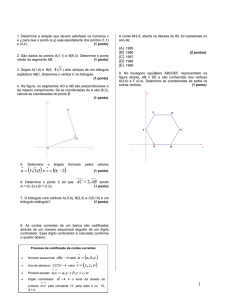
13-
̅̅̅̅
𝑨𝑪 é hipotenusa do triângulo da figura abaixo. Determine o valor de m e a área do
Encontre os valores dos pontos médios de A(- 5, 2) e B(3, 2).
14Os pontos P(2, 6) e Q(- 4, -1) são extremidades de um diâmetro da circunferência 𝝀.
Ache as coordenadas da circunferência do centro do raio de 𝝀.
15-
Esboce o gráfico e mostre que os pontos A(- 3, - 11), B(0, - 2) e C(5, 13) são colineares.
16- Verifique se os três pontos A(- 4, 0), B(- 1,- 2) e C(0, 6) são colineares.
17- (Fuvest –SP) Os vértices de um triângulo ABC, no plano cartesiano, sã: A(1, 0) B(0, 1) e
C(0, √𝟑). Então, o ângulo BÂC mede quanto?
18- Encontre a forma reduzida de cada reta:
A)
3x + 2y – 6 = 0
B)
X + y + 16 = 0
19- Obtenha a equação geral da reta r, que passa pelos pontos A(- 5, - 1) e B(2, 3).
20- Determine o coeficiente angular da reta r que passa pelos pontos (0, 2) e (5, 1). A seguir,
determine a equação reduzida de r.
21- Identifique se as retas r: 8x – 2y + 7 = 0 e s: y = 4x + 7 são paralelas ou secantes.
22 – Calcule a área do triângulo de vértices A(2, -4), B(- 3, 2) e (-1, -1).