A1___GEOMETRIA_ANALITICA___2009

1. Determine a relação que devem satisfazer os números x
e y para que o ponto (x,y) seja eqüidistante dos pontos (1,1)
e (3,4).
(1 ponto)
2. São dados os pontos A(1,1) e B(9,3). Determine o ponto
médio do segmento AB.
(1 ponto)
3. Sejam A(1,0) e B(5, 4 3 ) dois vértices de um triângulo
eqüilátero ABC. Determine o vértice C no triângulo.
(1 ponto)
4. Na figura, os segmentos AO e AB são perpendiculares e
de mesmo comprimento. Se as coordenadas de A são (6,3),
calcule as coordenadas do ponto B.
(1 ponto)
5.
Determine

o
ângulo
 e v  0; 2.
formado
u  3 3;3
pelos
A conta 643-5, aberta na década de 80, foi cadastrada no
ano de:
(A)
(B)
(C)
(D)
(E)
1985
1986
1987
1988
1989
(2 pontos)
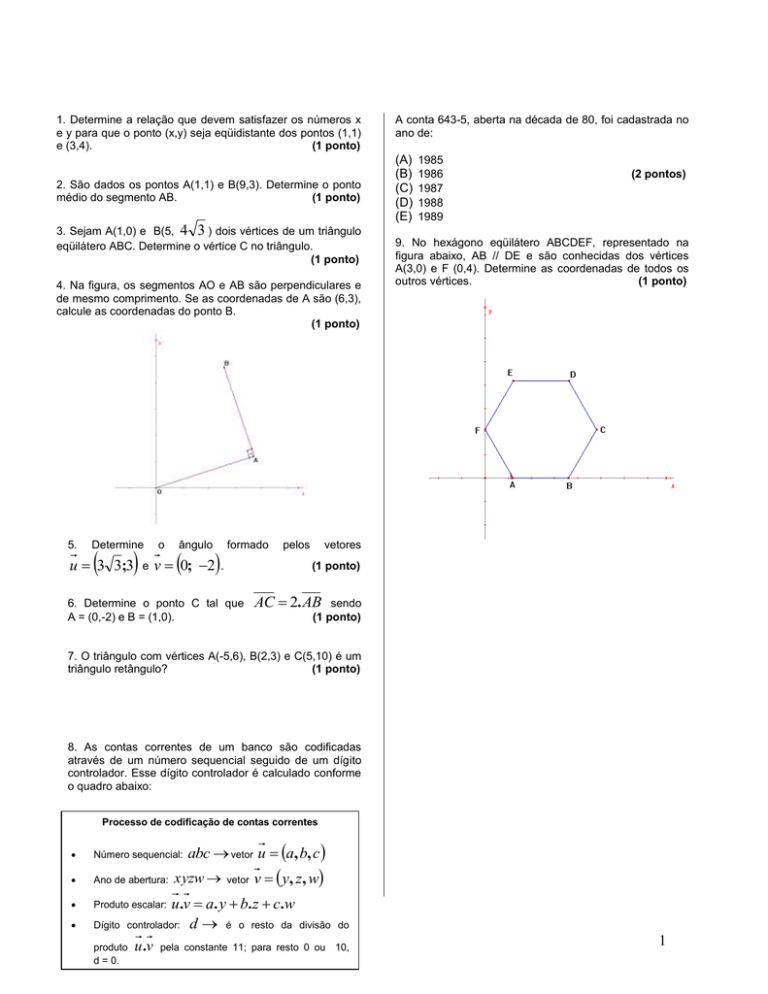
9. No hexágono eqüilátero ABCDEF, representado na
figura abaixo, AB // DE e são conhecidas dos vértices
A(3,0) e F (0,4). Determine as coordenadas de todos os
outros vértices.
(1 ponto)
vetores
(1 ponto)
6. Determine o ponto C tal que
A = (0,-2) e B = (1,0).
AC  2. AB
sendo
(1 ponto)
7. O triângulo com vértices A(-5,6), B(2,3) e C(5,10) é um
triângulo retângulo?
(1 ponto)
8. As contas correntes de um banco são codificadas
através de um número sequencial seguido de um dígito
controlador. Esse dígito controlador é calculado conforme
o quadro abaixo:
Processo de codificação de contas correntes

Número sequencial:

Ano de abertura:

Produto escalar:

abc  vetor u  a, b, c 
xyzw 
vetor
v   y, z, w
u.v  a. y  b. z  c.w
Dígito controlador: d  é o resto da divisão do
produto u.v pela constante 11; para resto 0 ou 10,
d = 0.
1