Matemática Mod 2.pmd

www.alunonota10.com
Funções Trigonométricas II
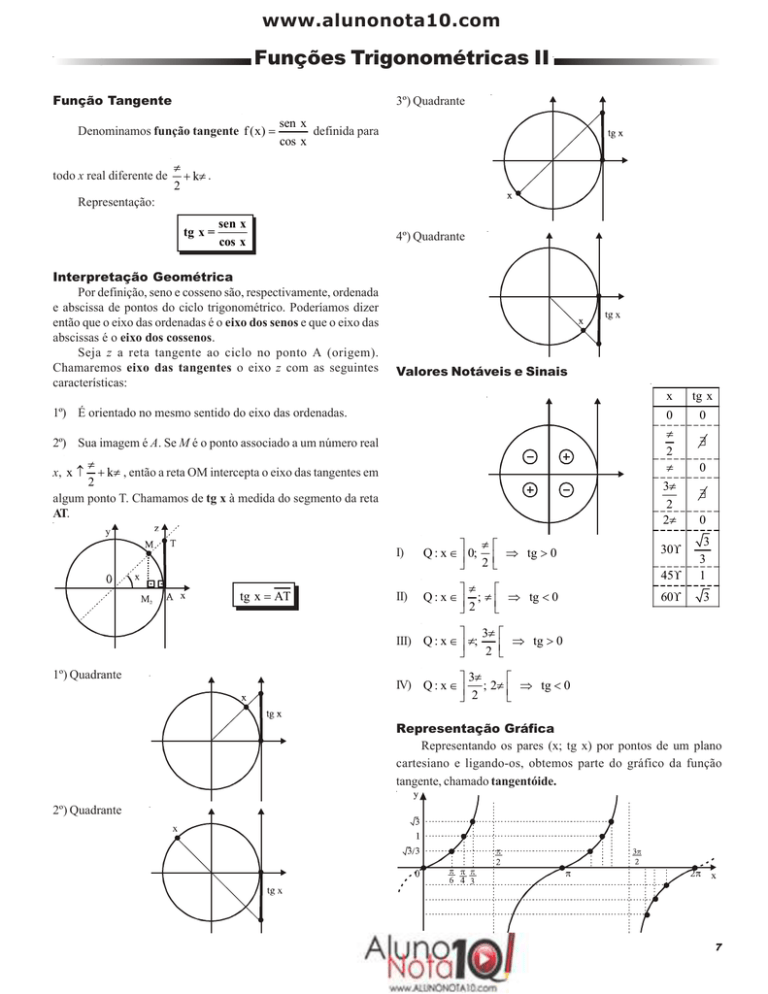
Função Tangente
3º) Quadrante
Denominamos função tangente f (x) =
todo x real diferente de
sen x
definida para
cos x
π
+ kπ .
2
Representação:
tg x =
sen x
cos x
Interpretação Geométrica
Por definição, seno e cosseno são, respectivamente, ordenada
e abscissa de pontos do ciclo trigonométrico. Poderíamos dizer
então que o eixo das ordenadas é o eixo dos senos e que o eixo das
abscissas é o eixo dos cossenos.
Seja z a reta tangente ao ciclo no ponto A (origem).
Chamaremos eixo das tangentes o eixo z com as seguintes
características:
4º) Quadrante
Valores Notáveis e Sinais
1º) É orientado no mesmo sentido do eixo das ordenadas.
2º) Sua imagem é A. Se M é o ponto associado a um número real
π
+ kπ , então a reta OM intercepta o eixo das tangentes em
2
algum ponto T. Chamamos de tg x à medida do segmento da reta
AT.
x, x ≠
tg x = AT
x
tg x
0
π
2
π
3π
2
2π
0
∃
0
∃
0
I)
 π
Q : x ∈  0;  ⇒ tg > 0
 2
30°
45°
II)
π

Q : x ∈  ; π  ⇒ tg < 0
2


3
3
1
60°
3
 3π 
III) Q : x ∈  π;
⇒ tg > 0
2 

1º) Quadrante
 3π

IV) Q : x ∈  ; 2π  ⇒ tg < 0
 2

Representação Gráfica
Representando os pares (x; tg x) por pontos de um plano
cartesiano e ligando-os, obtemos parte do gráfico da função
tangente, chamado tangentóide.
2º) Quadrante
7
www.alunonota10.com
Funções Trigonométricas II
Observemos que:
1) o
domínio
02. Para que valor de x, abaixo não existe tg 4x ?
da
função
tangente
é

π

D = R −  x x = + kπ  .
2


2) a imagem é R.
x≠
3)
a função tangente é periódica e de período p = π.
4)
5)
a função tangente não é limitada.
a tangente é função ímpar porque tg(-x) = -tg x, para todo
π
+ kπ .
2
Outras Funções Trigonométricas
Sabemos que:
cos x = 0 ⇔ x =
sen x = 0 ⇔ x = kp
π
+ kπ
2
cos x
1) Denominamos função cotangente à função f (x) =
sen x
definida para todo x real diferente de kπ.
cotg x =
cos x
sen x
a)
b)
c)
d)
e)
π
π/2
π/4
π/8
π/16
03. (UFPB) Entre 0° e 2590° existem vários arcos que admitem o
valor 1/2 para o seno, sendo precisamente:
a) 259 arcos
b) 14 arcos
c) 7 arcos
d) 15 arcos
e) Nada acima.
04. (UFPB) O contra-domínio da função tangente é:
a)
b)
c)
d)
e)
R
R - {x ∈ R | x = kπ}, k inteiro
{x ∈ R | x ≥ 0}
{x ∈ R | x = kπ}, k inteiro
Nenhm dos anteriores.
05. (UFPB) A medida, em radianos, de um ângulo de 2°3’ é:
a)
41π
3600
b)
23π
1800
1
sec x =
cos x
c)
41π
360
1
3) Denominamos função cossecante à função f (x) =
sen x
d)
41π
180
e)
23π
3600
2) Denominamos função secante à função f (x) =
1
definida
cos x
π
para todo x real diferente de + kπ .
2
definida para todo x real diferente de kπ.
cossec x =
1
sen x
06. (UFPB) A função f(x) = sen x é injetora no intervalo:


01. Determine o domínio de y = tg  2x − 3  .
a)
b)
c)
d)
e)
02. Determine o domínio de y = cossec 3x.
Gabarito:
π


(π/2; 2π)
(π/2; 3π/2)
(0; π)
(π; 2π)
≠ dos anteriores.
{

b) D =  x ∈ R x ≠
01. Dê o domínio das funções:
π

a) y = tg  x − 
2

b) y = 2 tg (2x - π)
8

02.
03.
04.
05.
06.
}
a) D = x ∈ R x ≠ π + kπ, k ∈ Z
01.
d
d
a
a
b
3π kπ

+
, k ∈ Z
4
2
