Números Complexos na Forma Trigonométrica

145
AULA 34 - NÚMEROS COMPLEXOS
Para
ilustrar,
calcularemos
o
argumento
de
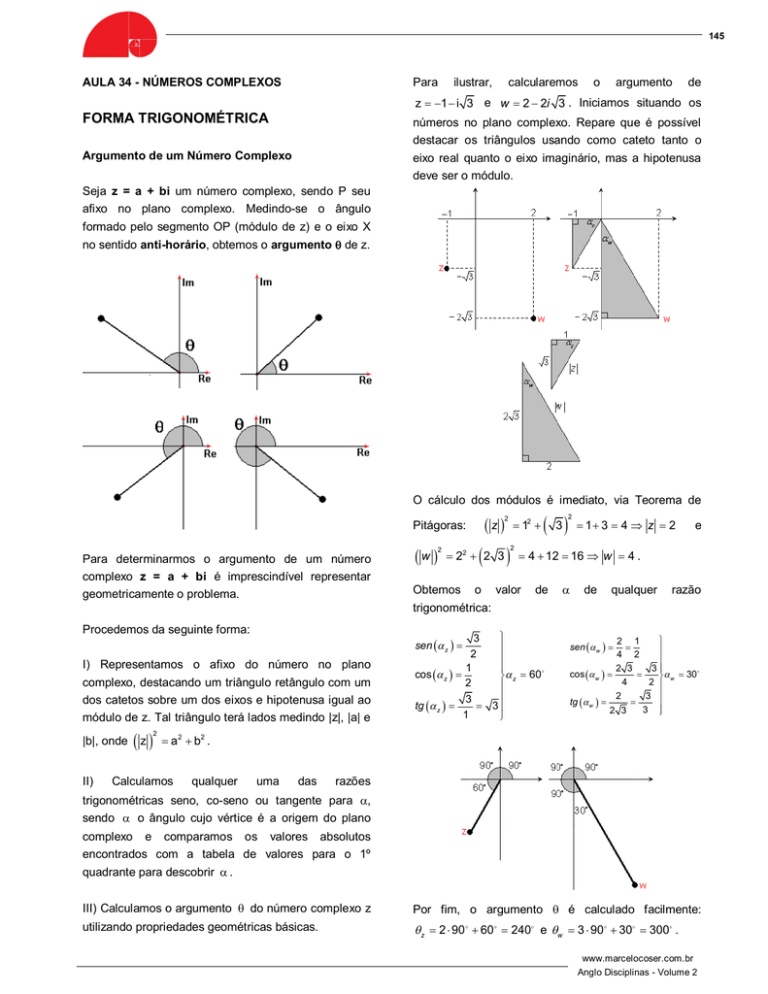
z  1  i 3 e w  2  2i 3 . Iniciamos situando os
FORMA TRIGONOMÉTRICA
números no plano complexo. Repare que é possível
destacar os triângulos usando como cateto tanto o
Argumento de um Número Complexo
eixo real quanto o eixo imaginário, mas a hipotenusa
deve ser o módulo.
Seja z = a + bi um número complexo, sendo P seu
afixo no plano complexo. Medindo-se o ângulo
formado pelo segmento OP (módulo de z) e o eixo X
no sentido anti-horário, obtemos o argumento  de z.
O cálculo dos módulos é imediato, via Teorema de
z
2
 22  2 3


o
valor
Pitágoras:
Para determinarmos o argumento de um número
complexo z = a + bi é imprescindível representar
geometricamente o problema.
w 
2
Obtemos
 12 
2
 3
2
 1 3  4  z  2
e
 4  12  16  w  4 .
de

de
qualquer
razão
trigonométrica:
Procedemos da seguinte forma:





  z  60


3
tg  z  
 3
1

3
2
1
cos  z  
2
sen  z  
I) Representamos o afixo do número no plano
complexo, destacando um triângulo retângulo com um
dos catetos sobre um dos eixos e hipotenusa igual ao
módulo de z. Tal triângulo terá lados medindo |z|, |a| e
|b|, onde
II)
z
2

2 1


4 2

2 3
3

cos  w  

  w  30
4
2 
2
3 
tg  w  


3 
2 3
sen  w  
 a 2  b2 .
Calculamos
qualquer
uma
das
razões
trigonométricas seno, co-seno ou tangente para ,
sendo  o ângulo cujo vértice é a origem do plano
complexo e comparamos os valores absolutos
encontrados com a tabela de valores para o 1º
quadrante para descobrir  .
III) Calculamos o argumento  do número complexo z
Por fim, o argumento  é calculado facilmente:
utilizando propriedades geométricas básicas.
 z  2  90  60   240 e w  3  90  30  300 .
www.marcelocoser.com.br
Anglo Disciplinas - Volume 2
146
O que acabamos de fazer, na verdade, foi obter as
coordenadas polares equivalentes a
 1,  3 
e
 2,  2 3  . Para o primeiro ponto, um deslocamento
horizontal de 1 para a esquerda e outro vertical de
3
para baixo equivalem a girar 240º no sentido antihorário e avançar 2 a partir da origem. Para o segundo
ponto, um deslocamento horizontal de 2 para a
esquerda e outro vertical de
para baixo
2 3
equivalem a girar 300º no sentido anti-horário e
avançar 4 a partir da origem.
Qualquer coordenada retangular
coordenada polar
 ,  
 a, b 
EXERCÍCIOS DE AULA
01) (UFAL) Sejam os números complexos z1  3  9i e
z2  5  7i .
O argumento principal do número
complexo z1  z2 é:
a) 90º
b) 120º
c) 135º
d) 145º
e) 180º
possui uma
equivalente, sendo  o
avanço a partir da origem e  o giro no sentido antihorário.
02)
Determinar

a
forma
algébrica
de

z = 2 cos120  i.sen120 .
Forma Trigonométrica de um Complexo
Seja z = a + bi um número complexo, sendo P seu
afixo no plano complexo.
Do triângulo retângulo destacado, tem-se cos 
sen 
b
.
z
Logo,
a  z  cos 
e
a
e
z
b  z  sen .
Substituindo essas relações em z = a + bi, temos que
z  z  cos   z  sen  i  z   cos   i  sen  . Assim,
a forma trigonométrica (ou polar) de z é
z = z .  cosθ + i.senθ 
www.marcelocoser.com.br
Anglo Disciplinas - Volume 2
147
Multiplicação e Divisão de Números Complexos na
Forma Trigonométrica
Uma das principais razões para que se converta um
número complexo da forma algébrica para a
trigonométrica é a facilidade de se multiplicar e dividir
números nessa forma.
EXERCÍCIOS DE AULA

 

03) Dado z  2  cos
 i.sen  , calcular z 4 na
12
12 

forma algébrica.
O produto z1  z2 , sendo z1  z1   cos 1  i  sen1  e
z 2  z 2  cos 2  i  sen 2  , é obtido a partir da soma
de arcos na trigonometria:
zn  z n  cos n     i  sen n   
04) Calcular a forma algébrica de z 
A divisão
modo
z   cos 1  i  sen1 
z1
 1
z2
z2   cos  2  i  sen 2 
análogo,
partindo
da
12
3 i

.
é obtida de
multiplicação
denominador e do numerador por z2

do
e também
utilizando conceitos trigonométricos, de modo que
05) Qual o menor valor inteiro positivo de n tal que
.
n
z  1  i  seja um número real negativo?
Assim,
z1 . z2  z1  z2  cos  1   2   i  sen  1   2 
z
z1
 1  cos  1   2   i  sen  1   2 
z2 z2
Ou seja, quando multiplicamos dois números
complexos na forma trigonométrica, multiplicamos os
seus módulos e somamos seus argumentos; quando
dividimos dois números complexos na forma
trigonométrica, dividimos os seus módulos e
subtraímos seus argumentos.
www.marcelocoser.com.br
Anglo Disciplinas - Volume 2
148
Raízes Complexas
Ou seja, existem, como poderíamos prever, três
soluções
A relação obtida em um dos exercícios de aula para
potências inteiras positivas pode ser ampliada para
qualquer potência. Assim, para n real, tem-se que
n
z n = z  cos n    + i  sen n   
Essa relação (conhecida por Fórmula de De Moivre)
apresenta resultados particularmente interessantes
1
, ou seja, para o
n
cálculo de raízes complexas de um número, seja ele
real ou não.
para potências racionais do tipo
Para ilustrar, iremos calcular as raízes cúbicas de 8.
Ou seja, resolver a equação z 3  8 . Inicialmente, a
para
a
equação
z3  8 ,

obtidas
de


 k  360 
 k  360  
z   8   cos 
  i  sen 
 :
3


 3


1
3

 2  cos120
 2   cos 240

k=0

z1  2  cos 0  i  sen 0  2
k=1

z2
k=2

z3

 i  sen240   1  i

 i  sen120  1  i 3


3
Esse resultado por si só já é surpreendente, mas é
ainda mais interessante analisar as conseqüências
geométricas que derivam dele. Representando no
plano complexo essas três soluções, elas
correspondem aos vértices de um triângulo eqüilátero
inscrito num círculo de raio 2.
única solução para essa equação seria z = 2, pois
23  8 . No entanto, se incluirmos números complexos
como
possíveis
soluções,
essa
resposta
está
incompleta.
Convertendo
algébrica
8
da
8  0  i 
forma
para a
forma trigonométrica, obtemos


8  cos0  i  sen 0 .
Porém, 8   cos0  i  sen 0  pode ser reescrito como




8  cos 0  k  360  i  sen 0  k  360  , k   ,


a
partir de sucessivos giros de 360º partindo da posição
inicial   0 , sempre gerando arcos equivalentes.
Assim, z 3  8   z
1
3 3

1
3
1
3
  8   z   8  , que por sua
vez, aplicando a Fórmula de De Moivre, vale
1 
 k  360
z   8  3  cos 
 3


 k  360
  i  sen 

 3

  . A tabela

abaixo apresenta o valor do argumento para alguns
valores de k:
Logo, equações na forma z n  w terão n soluções
como
zk 
n

   k  360 
   k  360  
w  cos 
  i  sen 
 ,
n
n





sendo k = 0, 1, 2, ..., n - 1. Porém, para que esse
teorema seja devidamente compreendido e facilmente
posto em prática, ele deve ser entendido
geometricamente:
As n raízes complexas de um número w são vértices
de um polígono regular de n lados inscrito em um
círculo com raio igual ao módulo de qualquer uma
dessas raízes, se n > 2. Generalizando, podemos
resolver a equação z n = w
Observe que a partir de k = 2 os valores de  passam
a se repetir, dada a incidência de arcos equivalentes.
realizando sucessivas

rotações de
360
em uma raiz conhecida.
n
www.marcelocoser.com.br
Anglo Disciplinas - Volume 2
149
EXERCÍCIOS DE AULA:
08) Uma das raízes cúbicas de x é  3  i . Calcule as
demais raízes e determine o valor de x.
06) A equação x 5  32  0 possui quantas raízes com
parte real positiva?
07) Calcule a área do polígono convexo tendo como
4
vértices as raízes da equação x - 81 = 0 no plano
complexo.
EXERCÍCIOS
01) (UFRGS) Se z  3  i e z´ 3  3.i , então z . z´
tem módulo e argumento, respectivamente, iguais a:
a) 2 3 e 30º
b) 3 2 e 30º
d) 4 3 e 30º
e) 4 3 e 60º
c) 3 2 e 60º
02) (UFRGS) Considere as afirmações seguintes:
I - O produto de dois números complexos conjugados
é um número real.
II - O módulo de um número complexo é um número
real não-negativo.
III - O argumento de qualquer número complexo da
forma z = bi (b ≠ 0) vale  / 2 .
Apenas está(ão) correta(s):
a) II
b) II e III
c) I e II
d) I e III
e) I, II e III
www.marcelocoser.com.br
Anglo Disciplinas - Volume 2
150
03) (UFRGS) A forma trigonométrica de z 
a) 2(cos135  i.sen135 )
1  i
é:
i
b) 2(cos 45  i.sen45 )
d)
c) cos120  i.sen120 )
2(cos315  i.sen315 )
e) 2(cos 225  i.sen225 )
04) (UFRGS) Na figura, o número complexo z é:
a)
2
2

i
2
2
c)
2  2.i
e)
2  2.i
05)
b) 
2
2

i
2
2
d)  2  2.i
(UFRGS)
Considere
o
ponto
P(5 3,5)
representado
no
gráfico
abaixo.
A
forma
trigonométrica do número complexo z, representado
pelo ponto P, é:
a) 10(cos30º + i.sen30º)
b) 5(cos30º + i.sen30º)
c) 10(cos45º + i.sen45º)
d) 5(cos45º + i.sen45º)
e) 5(cos60º + i.sen60º)
06) (UFRGS) Considere z1 = -3 + 2i e z2 = 4 + i. A
representação trigonométrica de z1 + z 2 é:



a)  cos  i.sen 
4
4

b)



2  cos  i.sen 
4
4

3
3 

c)  cos
 i.sen
4
4 

d)
7
7 

2  cos
 i.sen
4
4 

7
7 

e)  cos
 i.sen
4
4 

07) (UFRGS) O argumento do número complexo z é

, e o seu módulo é 2. A forma algébrica de z é:
6
a) -i
b) i
c)
3 i
d)
3 i
e)
3 i
www.marcelocoser.com.br
Anglo Disciplinas - Volume 2
151
08) (FGV) A figura indica a representação dos
números
e
z1
no
z2
plano
complexo.
Se
z1  z2  a  bi , então a + b é igual a:


b) 2   3  1
c) 2  1  3 
d) 2   3  1
e) 4  1  3 
a) 4  1  3
09) (UFRGS) O valor de
a) 64 - 64i
b) -64i

3 i
c) 64i

6
é:
d) -64
e) 64
10) (UFRGS) Os vértices de um triângulo são os
pontos do plano que representam as raízes cúbicas
complexas de 27. O perímetro desse triângulo é:
a) 3 3
b) 6 3
c) 9
d) 9 3
e) 27
11) (UFRGS) O ângulo formado pelas representações
geométricas dos números complexos z  3  i e z4 é:
a)

6
b)

4
c)

3
d)

2
e) 
12) (UFRGS) Os vértices do hexágono da figura
representam geometricamente as raízes sextas de um
número complexo. Sabendo-se que o vértice C
representa geometricamente o complexo -1 + i, o
vértice A representa geometricamente o complexo:
a)

 

2.  cos  i .sen 
12
12 

b)

 

2.  cos  i .sen 
12
12 

c)



2.  cos  i .sen 
6
6

d)



2.  cos  i .sen 
6
6

e)



2.  cos  i .sen 
4
4

www.marcelocoser.com.br
Anglo Disciplinas - Volume 2
152
13) (UFRGS) A região hachurada da figura é parte do
plano complexo e simétrica em relação à origem O. Se
o número complexo z, de argumento θ, está na região,
então:
a) z  2 e 



2
2
b) z  2 e 



2
2
c) z  2 e  

2
3
5
7 

d) z  2 e    
ou

4
4
4
4 

3
5
7 

e) z  2 e    
ou

4
4
4 
4
14) (UFRGS) (1 + i)15 é igual a:
a) 64(1 + i)
d) 256(-1 + i)
b) 128(1 - i)
e) 256(1 + i)
c) 128(-1 - i)
15) (UFRGS) Se u é um número complexo, as
representações gráficas de u e i.u podem ser:
a)
b)
c)
d)
e)
16) (UFRJ) Determine o menor inteiro n  1 para o
qual

3 i

n
é um número real positivo.
17) (UNIRIO) Uma das raízes cúbicas de um número
complexo é 2   cos300   i  sen 300  . Determine o
conjugado da soma das outras raízes.
www.marcelocoser.com.br
Anglo Disciplinas - Volume 2
153
18) (FUVEST) Dado o número complexo z  3  i
qual é o menor valor do inteiro n  1 para o qual z n é
um número real?
a) 2
b) 4
c) 6
d) 8
e) 10
19) (ITA) Considere, no plano complexo, um polígono
regular cujos vértices são as soluções da equação
z 6  1. Sua área, em unidades de área, é igual a:
a)
3
c) 
b) 5
d)
3 3
2
e) 2
20) (PUCCAMP) Seja o número complexo z 
4i
.A
1 i
forma trigonométrica de z é:



a) 2 2  cos  i  sen 
4
4

3
3 

d) 2  cos
 i  sen

4
4 

7
7 

b 2 2  cos
 i  sen

4
4 

7
7 

e) 2  cos
 i  sen

4
4 




c) 4  cos  i  sen 
4
4

21) (UFF) O número complexo z = a + bi, |z| > 1, a > b,
está representado geometricamente a seguir (figura
1). A figura que pode representar, geometricamente, o
número complexo z² é:
22) (UEL) O produto dos números complexos
cos




 i  sen e cos  i  sen é igual a:
6
6
3
3
a)
3 i
b)
2i
c)
2 i
d) 1
e) i
www.marcelocoser.com.br
Anglo Disciplinas - Volume 2
154
23) (UFRGS) Considere z1  3  2i e z2  4  i . A
29) (UNIRIO) Se z1 e z2 são números complexos
representação trigonométrica de
representados pelos seus afixos no Plano de Argand-
z1
somada ao
Gauss acima, então z3  z1  z2
conjugado de z2 é:
escrito na forma
trigonométrica é:
a) cos
b)


 i  sen
4
4
7
7 

d) 2   cos
 i  sen

4
4 




2   cos  i  sen 
4
4

e) cos


b) 2   cos 315  i  sen315 
c) 2 2   cos 45  i  sen 45 
d) 2 2   cos135  i  sen135 
a)
7
7
 i  sen
4
4



3
3
c) cos
 i  sen
4
4



2 2  cos 225  i  sen 225 
25) (UFSM) Dados dois números complexos na forma
e
w  s   cos   i  sen   ,

e)
24) Calcule as raízes cúbicas complexas de 64 na
forma trigonométrica.
z  r   cos   i  sen 
2  cos 225   i  sen 225 
30) Dado z 

1 i 3
, calcule z100.

2
2
pode-se afirmar que z.w é igual a:
a) rs  cos    sen  
b) rs  cos      i  sen    
c) rs  cos      i  sen     
d)  r  s    cos   cos   i  sen  sen  
e)  r  s   cos      i  sen    
26)
(UNESP)
z  cos
a) -i
Considere
o
número
complexo


 i  sen . O valor de z 3  z 6  z12 é:
6
6
b)
1 i 3

2
2
c) i - 2
d) i
GABARITO
01
E
02
C
03
A
04
D
05
A
06
B
07
E
08
A
09
D
10
D
11
D
12
B
13
D
14
B
15
A
16
12
18
C
19
D
22
E
23
B
e) 2i
27) Se u = cos3º + i.sen3º, v = cos11º + i.sen11º e
w = cos4º + i.sen4º, qual a forma algébrica de
u  v7
w5
?
28) (MACK) As representações gráficas dos
complexos z tais que z³ = -8 são os vértices de um
triângulo:
17
a) inscrito numa circunferência de raio 1.
b) que tem somente dois lados iguais.
c) eqüilátero de lado 2.
24
20
1  i 3
A
21
C
 
4 , 4 cos120  i.sen120 , 4 cos 240  i.sen240

25
B
26
D
27
28
E
29
E
30
d) eqüilátero de altura 2 3 .
e) de área 3 3 .

1 i 3

2
2

1 i 3

2
2
www.marcelocoser.com.br
Anglo Disciplinas - Volume 2