Aula 25 - Funções Trigonométricas

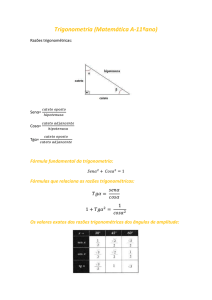
1. Funções trigonométricas
UNIVERSIDADE DO ESTADO DE MATO GROSSO
CAMPUS UNIVERSITÁRIO DE SINOP
FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS
CURSO DE ENGENHARIA CIVIL
DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I
Definição pelo Triângulo Retângulo: 0 <θ<π/2
cat. op.
hip.
csc θ =
cat . adj .
hip.
cat . op.
tg θ =
cat . adj .
sec θ =
sen θ =
cos θ =
Funções Trigonométricas
hip.
cat. op.
hip.
cat . adj .
cat . adj .
cot θ =
cat. op.
Prof.: Rogério Dias Dalla Riva
4
Funções Trigonométricas
1. Funções trigonométricas
1.Funções Trigonométricas
Definição como Função Circular: θ é um ângulo
arbitrário em posição padrão e (x, y) é um ponto no
lado terminal do ângulo.
2.Identidades Trigonométricas
3.Cálculo de Funções Trigonométricas
4.Resolução de Equações Trigonométricas
y
r
x
cos θ =
r
y
tg θ =
x
sen θ =
r
y
r
sec θ =
x
x
cot θ =
y
csc θ =
5
2. Identidades trigonométricas
1. Funções trigonométricas
Há duas maneiras usuais de encarar o estudo da
trigonometria. Em uma delas, definem-se as funções
trigonométricas como razões de dois lados de um
triângulo retângulo. Em outra, tais funções são
definidas em termos de um ponto no lado terminal de
um ângulo arbitrário. Definem-se a seguir, de ambos
os pontos de vista, as seis funções trigonométricas.
3
Na segunda definição das seis funções
trigonométricas, o valor de r é sempre positivo.
Decorre daí que os sinais das funções trigonométricas
são determinados a partir dos sinais de x e y.
sen θ
cos θ
cos θ
cot θ =
sen θ
1
cot θ =
tg θ
tg θ =
1
cos θ
1
cs c θ =
sen θ
sec θ =
6
1
2. Identidades trigonométricas
2. Identidades trigonométricas
Além disso, como
Ângulo Duplo
2
2
x +y
r
y x
s e n2 θ + cos2 θ =   +   =
= 2 =1
r2
r
r  r 
2
2
2
s e n 2θ = 2sen θ cos θ
obtemos a Identidade de Pitágoras.
cos 2θ = cos2 θ − sen 2 θ
cos 2θ = 2cos2 θ − 1 = 1 − 2sen 2 θ
Nota: Usa-se o símbolo sen2θ para representar
(sen θ)2.
7
2. Identidades trigonométricas
2. Identidades trigonométricas
Identidades Pitagóricas
Fórmulas de Redução
s e n ( −θ ) = −sen θ
s e n2 θ + cos2 θ = 1
cos ( −θ ) = cos θ
tg ( −θ ) = −tg θ
s e n θ = −sen (θ − π )
tg θ + 1 = sec θ
2
10
2
cot 2θ + 1 = csc 2 θ
cos θ = − cos (θ − π )
tg θ = tg (θ − π )
8
2. Identidades trigonométricas
11
2. Identidades trigonométricas
Soma ou Diferença de Dois Ângulos
Ângulo Metade
s e n (θ ± φ ) = sen θ cos φ ± cos θ sen φ
1
(1 − cos 2θ )
2
1
cos2 θ = (1 + cos 2θ )
2
s e n2 θ =
cos (θ ± φ ) = cos θ cos φ ∓ sen φ sen θ
tg θ ± tg φ
tg (θ ± φ ) =
1 ∓ tg θ tg φ
9
12
2
3. Cálculo de funções trigonométricas
3. Cálculo de funções trigonométricas
Exemplo 1: Calcule o seno, o cosseno e a tangente de
π/3.
Inicialmente, tracemos o
ângulo θ = π/3 em posição
padrão, conforme a figura ao lado.
A seguir são apresentados os senos, cossenos e
tangentes de vários ângulos usuais.
Medida em graus de θ
0
30o
Medida em radianos de θ
0
sen θ
0
cos θ
tg θ
13
3. Cálculo de funções trigonométricas
45o
60o
90o
π/6
π/4
π/3
π/2
1/2
2
3
1
3
2
0
3
2
3
2
2
1
2
1/2
3
1
0
nãodefinido
16
3. Cálculo de funções trigonométricas
Exemplo 1: Calcule o seno, o cosseno e a tangente de
π/3.
Como π/3 radianos correspondem a 60o, podemos imaginar um triângulo equilátero
com lados de comprimento 1 e
θ como um de seus ângulos.
Como a altura do triângulo
bissecciona sua base, sabemos
que x = ½. Assim, pelo Teorema
de Pitágoras, temos
Para entender a utilização dos valores da
tabela anterior a ângulos em quadrantes que não o
primeiro, valemo-nos do conceito de ângulo de
referência, conforme a figura acima, juntamente com
o sinal adequado do quadrante.
14
3. Cálculo de funções trigonométricas
17
3. Cálculo de funções trigonométricas
Exemplo 1: Calcule o seno, o cosseno e a tangente de
π/3.
2
 1
y = r 2 − x2 = 1−   =
2
3
3
=
4
2
Portanto:
π
3
=
y
=
r
3
2 = 3
1
2
1
π x
1
cos = = 2 =
3 r
1
2
3
π y
2 = 3
tg = =
1
3 x
2
sen
O ângulo de referência para um ângulo θ é o
menor ângulo positivo entre o lado terminal de θ e o
eixo x. Por exemplo, o ângulo de referência para 135o
é 45o, e o ângulo de referência para 210o é 30o.
15
18
3
3. Cálculo de funções trigonométricas
3. Cálculo de funções trigonométricas
Exemplo 2: Calcule: (a) sen 3π/4, (b) tg 330o e
(c) cos 7π/6.
Como o ângulo de
referência para 3π/4 é π/4
e o seno é positivo no
segundo quadrante, podemos
escrever
3π
π
2
sen
4
= sen
4
=
2
Exemplo 3: Calcule: (a) sen (-π/3), (b) sec 60o,
(c) cos 15o, (d) sen 2π, (e) cot 0o e (f) tg (9π/4).
(a) Pela fórmula de redução sen (-θ) = - sen θ.
π
3
 π
sen  −  = −sen = −
3
2
 3
(b) Pela fórmula do inverso, sec θ = 1/cosθ.
sec 60o =
1
1
=
=2
cos 60o 1/ 2
19
22
3. Cálculo de funções trigonométricas
3. Cálculo de funções trigonométricas
Exemplo 2: Calcule: (a) sen 3π/4, (b) tg 330o e
(c) cos 7π/6.
Como o ângulo de
referência para 330o é 30o e
a tangente é negativa no
quarto quadrante, podemos
escrever
tg 330o = −tg 30o = −
3
3
Exemplo 3: Calcule: (a) sen (-π/3), (b) sec 60o,
(c) cos 15o, (d) sen 2π, (e) cot 0o e (f) tg (9π/4).
(c) Pela fórmula da diferença cos (θ - φ) = cos θ cos φ
+ sen θ sen φ.
(
)
cos15o = cos 45o − 30o = cos 45o cos30o + sen 45o sen30o =
2 3
2 1
=
⋅
+
⋅ =
2 2
2 2
6+ 2
4
(d) Como o ângulo de referência para 2π é 0,
sen 2π = sen 0 = 0
23
20
3. Cálculo de funções trigonométricas
3. Cálculo de funções trigonométricas
Exemplo 2: Calcule: (a) sen 3π/4, (b) tg 330o e
(c) cos 7π/6.
Como o ângulo de
referência para 7π/6 é π/6
e o cosseno é negativo no
terceiro quadrante, podemos escrever
cos
7π
π
3
= − cos = −
6
6
2
Exemplo 3: Calcule: (a) sen (-π/3), (b) sec 60o,
(c) cos 15o, (d) sen 2π, (e) cot 0o e (f) tg (9π/4).
(e) Utilizando a fórmula do inverso, cotg θ = 1/tg θ e o
fato de que tg 0 = 0, concluímos que cotg 0 não é
definida.
(f) Como o ângulo de referência para 9π/4 é π/4 e a
tangente é positiva no primeiro quadrante
tg
21
9π
π
= tg = 1
4
4
24
4
3. Cálculo de funções trigonométricas
3. Cálculo de funções trigonométricas
Exemplo 4: Um agrimensor de pé, está a 50 pés de
distância da base de uma grande árvore. Ele mede o
ângulo de elevação em relação ao topo da árvore e
obtém 71,5o. Qual é a altura da árvore?
Utilizando a função inversa da tangente em uma
calculadora, podemos determinar θ ≈ 73,7o Assim,
α/2 ≈ 180o - 73,7o = 106,3o, o que implica que
α ≈ 212,6o. Em outras palavras, o ângulo total de sua
visão periférica é da ordem de 212,6o.
y
x
y = x ⋅ tg 71,5o
y ≈ 50 ⋅ 2,98868
y ≈ 149,4 pés
tg 71,5o =
25
28
4. Resolução de equações trigonométricas
3. Cálculo de funções trigonométricas
Exemplo 5: Para medir a extensão de sua visão
periférica, fique em pé, à distância de 1 pé do canto
de uma sala, olhando para o canto. Faça com que outra
pessoa mova um objeto ao longo da parede, até que
você mal possa vê-lo. Se o objeto está a 2 pés do
canto, conforme a figura seguinte, qual é o ângulo
total de sua visão periférica?
Considere, por exemplo, a equação sen θ = 0.
Sabemos que θ = 0 é uma solução. Por outro lado, no
Exemplo 3d, vimos que θ = 2π é outra solução. Mas
estas não são as únicas soluções. Na verdade, esta
equação tem um número infinito de soluções. Qualquer
um dos valores seguintes de θ serve:
…, − 3π , − 2π , − π , 0, π , 2π , 3π , …
Para simplificar a situação, costumamos
restringir a busca de soluções ao intervalo 0 ≤ θ ≤ 2π .
29
26
3. Cálculo de funções trigonométricas
4. Resolução de equações trigonométricas
Seja α o ângulo total de sua visão periférica.
Conforme a figura abaixo, podemos modelar a
situação física com um triângulo retângulo isósceles
cujos catetos têm 21/2 pés cada um e cuja hipotenusa
tem 2 pés. No triângulo, o ângulo θ é dado por
tg θ =
tg θ =
Exemplo 6: Resolva cada equação em relação a θ.
Suponha 0 ≤ θ ≤ 2π .
(a) sen θ = −
3
2
( b ) cos θ = 1
y
x
(c ) tg θ = 1
2
2 −1
tg θ ≈ 3,414
27
30
5
4. Resolução de equações trigonométricas
4. Resolução de equações trigonométricas
3
(a) Para resolver a equação sen θ = −
, notemos pri2
meiro que
Exemplo 7: Resolva, em relação a θ, a equação
cos 2θ = 2 − 3sen θ ,
0 ≤ θ ≤ 2π
Podemos utilizar a identidade do ângulo duplo
sen
π
3
=
cos 2θ = 1 − 2sen 2 θ
3
2
Para escrever a equação como segue:
cos 2θ = 2 − 3sen θ
Como o seno é negativo no terceiro e quarto
quadrantes, devemos procurar valores de θ nesses
quadrantes que tenham ângulo de referência de
π/3. Os dois ângulos que satisfazem estes critérios
31
são: θ = π + π/3 = 4π/3 e θ = 2π - π/3 = 5π/3.
4. Resolução de equações trigonométricas
1 − 2sen 2 θ = 2 − 3sen θ
2sen 2 θ − 3sen θ + 1 = 0
(2sen θ − 1) ⋅ (sen θ − 1) = 0
34
4. Resolução de equações trigonométricas
(b) Para resolver cos θ = 1, notemos que cos 0 = 1 e
que, no intervalo [0, 2π], os únicos ângulos cujos
ângulos de referência são 0 são os ângulos 0, π e
2π. Destes, 0 e 2π têm cosseno 1. (O cosseno de π é
-1). Assim, a equação tem duas soluções:
Para 2sen θ - 1 = 0, temos sen θ = 1/2, que tem as
soluções
θ = π/6 e
θ = 5π/6.
Para sen θ - 1 = 0, temos sen θ = 1, que tem a solução
θ= π/2
Assim, para 0 ≤ θ ≤ 2π , as três soluções são
θ = 0 e θ = 2π
θ = π/6, π/2 e 5π/6
32
35
4. Resolução de equações trigonométricas
(c) Como tg π/4 = 1 e a tangente é positiva no primeiro
e no terceiro quadrantes, temos que as duas
soluções são:
θ = π/4 e θ = π + π/4 = 5π/4
33
6