2 - ceap

CENTRO DE ENSINO SUPERIOR DO AMAPÁ
Profº: Paulo Smith – MATEMÁTICA APLICADA I - 2º SEMESTRE/2010
FUNÇÃO POLINOMIAL DO 1O GRAU
2.2.1.
xv  
CONCEITO:
Chamamos de função do 1o grau a função
ax  b , com a, b números reais não nulos, e a  0
cuja ordenada y v  
2.2.2. CARACTERÍSTICAS IMPORTANTES
- A função do 1o grau é crescente quando a > 0 e é
decrescente quando a < 0.
- Conjunto do domínio: é o conjunto dos números reais.
ii) Quando a < 0 a função apresenta um ponto de máximo,
cuja ordenada y    é o valor máximo da função.
v
Im( f )  R
4a
2.2.3. RAIZ DA FUNÇÃO
É o valor de x quando f(x) = 0, assim temos que:
y  ax  b e y  0 logo
b
a

é o valor mínimo da função.
4a


Im( f )   y  R | y  

4
a

Conjunto imagem: é o conjunto dos números reais.
ax  b  0  ax  b  x  

4a
Logo:
D( f )  R
-
yv  
- Conjunto do domínio: D ( f )  R
- Conjunto imagem:
i) Quando a > 0 a função apresenta um ponto de mínimo,
f : R  R que associa a cada número real x, o número
real
b
2a
Logo:


Im( f )   y  R | y   
4a 

EXERCÍCIOS
Sendo a função f ( x)  ax  b com a, b  R e a  0 ,
determine os valores de a e b de modo que f(3) = 4 e f(-1) =
2.
2. Seja f a função definida por f ( x)  2 x  6 .
a) f (2) =?
b) Para que valor de x, f(x) = 100?
c) Para que valor de x, f (x) = 0?
3. Seja f uma função linear definida por y  5 x  6 .
a) f( 0 ) = ?
b) f( ½) = ?
c) f( 11 ) =?
d) Para que valores de x, f(x) = 0?
e) Para que valores de x, f(x) = ½?
4. Ache a equação que define a função do 1º grau. Tal que:
a) ( 2, 10 ) e ( 8, 1 )
b) f( 1 ) = 3 ; f( - 3 ) = 4
1.
2.2.4. GRÁFICO
O gráfico é uma reta que corta o eixo dos x passando pela
raiz e corta o eixo dos y passando pelo coeficiente linear
2.2.5. INEQUAÇÃO
Para resolver inequações do 1o grau é necessário determinar
o zero das funções, fazer estudo do sinal e, posteriormente,
determinar os valores de x que satisfazem essa inequação.
OBS:
Se a > 0, a função é crescente;
Se a < 0, a função é decrescente.
2.3. FUNÇÃO DO 2º GRAU (FUNÇÃO QUADRÁTICA)
2.3.1. CONCEITO
Chamamos de função quadrática a função f : R  R que
associa a cada número real x o número real
y  ax2  bx  c , com a, b e c reais e a  0.
2.3.2. GRÁFICO
É uma curva aberta à qual chamamos de parábola.
Se a > 0, essa parábola terá a concavidade voltada para cima.
Se a < 0, essa parábola terá a concavidade voltada para
baixo.
Dada a função y  2 x  3x  1 , determinar:
a) As raízes, caso existam;
b) As coordenadas do vértice;
c) O valor mínimo da função, pois a > 0;
d) O gráfico
6. Determine as raízes de cada uma das funções quadráticas:
2
5.
a)
2.3.3. RÍAZES OU ZEROS
São os valores de x para os quais y = 0
Então, se y = 0, temos que
ax 2  bx  c  0  x, 
b 
b 
e x,, 
2a
2a
Onde   b  4ac
2
2.3.4. VÉRTICE
É o ponto de interseção entre o eixo de simetria e a própria
parábola, isto é, é o ponto onde a parábola
muda de
sentido, onde as coordenadas são:
y  x 2  5x  4
y  7 x  21
b)
7. Representar graficamente as parábolas abaixo:
a)
y  x 2  3x  10
y  2  x2
b)
8. Determinar as coordenadas dos pontos de interseção entre
as curvas:
y  x 2  8 x  11; y  4
2
b) y   x  14; y  2  4 x
a)
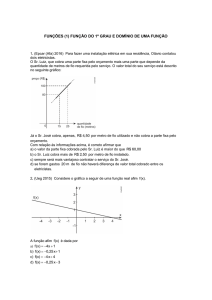
11. Um motorista paga R$ 45,50, por dia, pelo aluguel de um
carro que ele usa como táxi.
Sabe-se que o motorista cobra um valor fixo de b reais
CENTRO DE ENSINO SUPERIOR DO AMAPÁ
Profº: Paulo Smith – MATEMÁTICA APLICADA I - 2º SEMESTRE/2010
independentemente da distância a ser percorrida, mais a
real por cada quilômetro rodado.
O gráfico escreve o valor y, cobrado pelo taxista, em reais
em função do número x de quilômetros percorridos. Pedese:
a) O valor cobrado pelo taxista num percurso de 10 km.
b) O número de quilômetros que deve percorrer para que
o valor por ele cobrado seja suficiente apenas para o
pagamento do aluguel diário do carro.
12. Uma pedra é lançada verticalmente e sabe-se que no
instante t sua altura é dada por h(t )  20 t  5 t , 0  t  4 .
a) Esboce o gráfico de h.
b) Qual a máxima altura atingida pela pedra? Em que
instante essa altura é atingida? Suponha o tempo em
segundos e a altura em metros.
Duas locadoras A e B alugam carros populares nas seguintes
condições:
A – Uma taxa fixa de R$100,00 e R$ 0,20 por km rodado.
B – Uma taxa de R$ 40,00 e R$ 0,35 por km rodado.
a) Expresse o custo de locação em A por km rodado.
b) Expresse o custo de locação em B por km rodado.
c) Em que locadora é mais vantajosa a locação? Discuta
graficamente.
A tarifa de uma corrida de táxi é composta de uma parte
fixa, a bandeirada, e de uma parte variável que depende da
distância percorrida. Se a bandeirada estiver custando R$
3,20 e o quilômetro rodado R$ 0,18, pede-se:
a) Obtenha a função que determina uma corrida de táxi.
b) Quanto pagar-se-á por uma corrida de 10 km?
Calcule a soma das coordenadas do ponto de mínimo da
função y  2 x ²  x  3 .
Um foguete lançado acidentalmente de uma base militar,
cairá perigosamente de volta à Terra. A trajetória plana do
mesmo segue o gráfico de y  200 x  x ² .
Para interceptá-lo, da mesma base é lançado um míssil,
cuja trajetória é dada pela equação y  50 x .
A que altura do solo o foguete deverá ser atingido?
Obs.: “x” e “y” são medidas dadas em metros.
2
13.
14.
15.
16.