funções (1) função do 1º grau e domínio de uma função

FUNÇÕES (1) FUNÇÃO DO 1º GRAU E DOMÍNIO DE UMA FUNÇÃO
1. (Epcar (Afa) 2016) Para fazer uma instalação elétrica em sua residência, Otávio contatou
dois eletricistas.
O Sr. Luiz, que cobra uma parte fixa pelo orçamento mais uma parte que depende da
quantidade de metros de fio requerida pelo serviço. O valor total do seu serviço está descrito
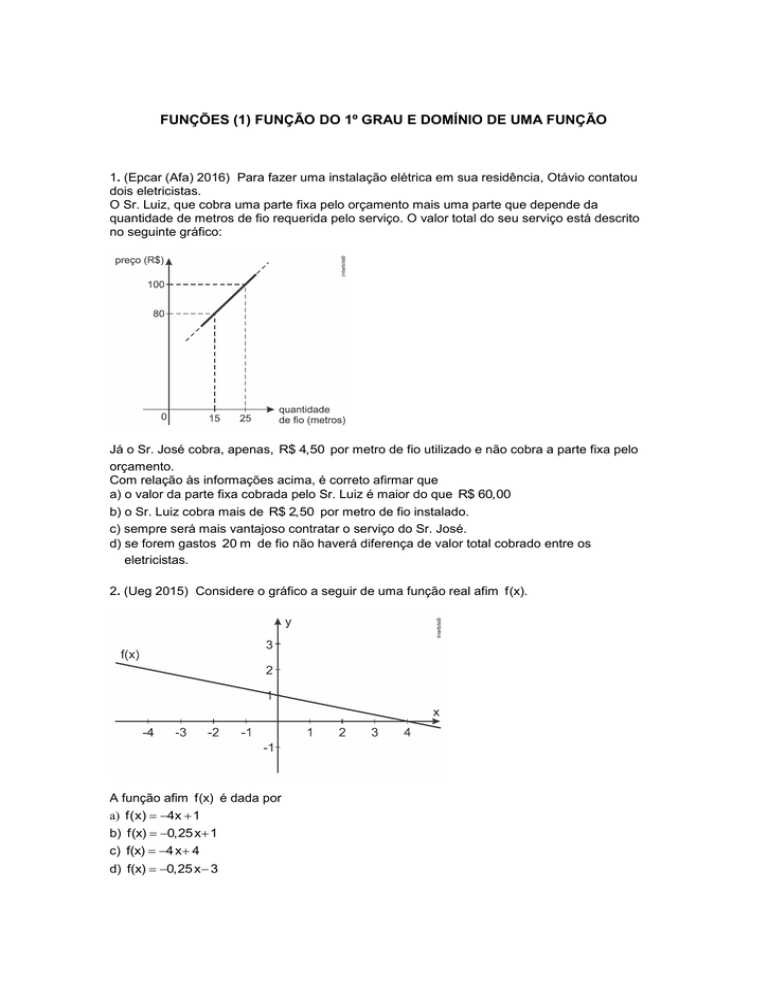
no seguinte gráfico:
Já o Sr. José cobra, apenas, R$ 4,50 por metro de fio utilizado e não cobra a parte fixa pelo
orçamento.
Com relação às informações acima, é correto afirmar que
a) o valor da parte fixa cobrada pelo Sr. Luiz é maior do que R$ 60,00
b) o Sr. Luiz cobra mais de R$ 2,50 por metro de fio instalado.
c) sempre será mais vantajoso contratar o serviço do Sr. José.
d) se forem gastos 20 m de fio não haverá diferença de valor total cobrado entre os
eletricistas.
2. (Ueg 2015) Considere o gráfico a seguir de uma função real afim f(x).
A função afim f(x) é dada por
a) f(x)  4x  1
b) f(x)  0,25 x 1
c) f(x)  4 x 4
d) f(x)  0,25 x 3
3. (Imed 2015) A função polinomial f, definida por f(x)  ax  b, que possui f( 2)  3 e
f(2)  1, intercepta o eixo das ordenadas em:
a) 3.
b) 2.
c) 1.
d) 0.
e) 1.
4. (G1 - cftmg 2014) O gráfico representa a função real definida por f(x) = a x + b.
O valor de a + b é igual a
a) 0,5.
b) 1,0.
c) 1,5.
d) 2,0.
5. (Ucs 2014) O salário mensal de um vendedor é de R$ 750,00 fixos mais 2,5% sobre o valor
total, em reais, das vendas que ele efetuar durante o mês.
Em um mês em que suas vendas totalizarem x reais, o salário do vendedor será dado pela
expressão
a) 750  2,5x.
b) 750  0,25x.
c) 750,25x.
d) 750   0,25x  .
e) 750  0,025x.
6. (Enem PPL 2014) Os sistemas de cobrança dos serviços de táxi nas cidades A e B são
distintos. Uma corrida de táxi na cidade A é calculada pelo valor fixo da bandeirada, que é de
R$ 3,45, mais R$ 2,05 por quilômetro rodado. Na cidade B, a corrida é calculada pelo valor
fixo da bandeirada, que é de R$ 3,60, mais R$ 1,90 por quilômetro rodado.
Uma pessoa utilizou o serviço de táxi nas duas cidades para percorrer a mesma distância de
6 km.
Qual o valor que mais se aproxima da diferença, em reais, entre as médias do custo por
quilômetro rodado ao final das duas corridas?
a) 0,75
b) 0,45
c) 0,38
d) 0,33
e) 0,13
7. (Uepb 2013) Uma função f definida de
todo x real. Se f(25)  125, f(1) é:
a) 6
b) 1
c) 25
d) 5
e) 4
em
satisfaz à condição f(5x)  5f(x) para
8. (Espcex (Aman) 2012) Considere a função real f(x), cujo gráfico está representado na figura,
e a função real g(x), definida por g  x   f  x  1  1.
 1
O valor de g    é
 2
a) 3
b) 2
c) 0
d) 2
e) 3
9. (Fgv 2011) O gráfico de uma função polinomial do primeiro grau passa pelos pontos de
coordenadas (x, y) dados abaixo.
x
0
m
6
7
y
5
8
14
k
Podemos concluir que o valor de k + m é:
a) 15,5
b) 16,5
c) 17,5
d) 18,5
e) 19,5
10. (G1 - ifal 2011) O domínio da função dada por f  x  
a) x  R 2  x  3.
b) x  R 2  x  3.
c) x  R 2  x  3.
d) x  R 2  x  3.
x2
3x
é
e) x  R x  3.
11. (Espcex (Aman) 2012) Considere as funções Reais f  x   3x, de domínio [4, 8] e
g  y   4y, de domínio [6, 9]. Os valores máximo e mínimo que o quociente
f x
g y
pode assumir
são, respectivamente
1
2
a)
e
2
3
1
b)
e1
3
3
4
c)
e
4
3
3
1
d)
e
4
3
1
e) 1 e
3
RESPOSTAS E SOLUÇÕES
1.[D]
Analisando as alternativas::
[A] INCORRETA. A parte fixa cobrada pelo Sr. Luiz corresponde ao ponto onde a reta
apresentada corta o eixo y (ou seja, quando a quantidade de fios é igual a zero). Para
encontrar a equação da reta, faz-se:
y  y1 
y2  y1
100  80
 (x  x1)  y  80 
(x  15)  y  2x  50
x2  x1
25  15
Assim, quando x  0, y  50. Logo, a parte fixa cobrada pelo Sr. Luiz equivale a R$ 50,00.
A alternativa é incorreta.
[B] INCORRETA. Pela equação do gráfico que representa o orçamento do Sr. Luiz, percebe-se
que ele cobra a parte fixa de R$ 50,00 mais R$ 2,00 a cada metro de fio instalado
(y  2x  50). Portanto, a alternativa é incorreta.
[C] INCORRETA. Se o Sr. José cobra R$ 4,50 por metro de fio utilizado, então a função de
seu orçamento é uma reta que passa pela origem e cuja equação é y  4,5x. Percebe-se,
pela análise dos coeficientes angulares, que a reta que representa o valor cobrado pelo Sr.
José começa na origem mas cresce mais rápido que a reta que representa o valor cobrado
pelo Sr. Luiz. Assim, até as duas retas se encontrarem, será vantajoso contratar os serviços
do Sr. José. Após isso, será mais vantajoso contratar os serviços do Sr. Luiz. Na figura a
seguir, a linha vermelha indica a função do orçamento do Sr. José. Portanto a alternativa é
incorreta.
[D] CORRETA. Substituindo a quantidade de fios x  20 nas duas equações, tem-se:
Sr. Luiz  y  2x  50  2  20  50  90
Sr. José  y  4,5x  4.5  20  90
Portanto, se forem gastos 20 metros de fio ambos os orçamentos resultarão em R$ 90,00.
A alternativa é correta.
2.[B]
Seja f(x)  ax  b, com a, b 
a lei de f. Do gráfico, é imediato que b  1. Ademais, sendo
x  4 o zero de f, temos 0  a  4  1, o que implica em a  0,25. Portanto, a lei de f é
f(x)  0,25x  1.
3.[C]
Se f( 2)  3 e f(2)  1, então podemos escrever o sistema:
2a  b  3

2a  b  1
2b  2  b  1
A função f(x)  ax  b irá interceptor o eixo das ordenadas quando x  0, ou seja, quando
f(0)  0a  b  f(0)  b  1.
4.[C]
Como o gráfico de f intersecta o eixo das ordenadas em (0, 3), segue-se que b  3. Além
disso, o gráfico de f intersecta o eixo das abscissas em (2, 0.) Logo,
0  a23  a  
3
2
e, portanto, a  b  
3
 3  1,5.
2
5.[E]
Desde que 2,5%  0,025, segue-se que o resultado é 750  0,025x.
6.[E]
Sejam c A e cB , respectivamente, as médias do custo por quilômetro rodado nas cidades A e
B, considerando uma corrida de 6km. Tem-se que
3,45
3,6
 1,9 
6
6
0,15
 0,15 
6
 0,13.
c A  cB  2,05 
7.[D]
Como f(5x)  5f(x), para todo x real, segue-se que f é linear, com f(x)  5x. Portanto,
f(1)  5  1  5.
8.[D]
Como o gráfico de f é uma reta, segue que f(x)  ax  b. Do gráfico, temos que b  2 e
2
2
e, portanto, f(x)  x  2.
3
3
2  3
 1
 3
Desse modo, g     f     1       2  1  2.
 2
3  2
 2
f(3)  0. Logo, 0  3a  2  a 
9.[C]
Seja f a função afim definida por f(x)  ax  b, cujo gráfico passa pelos pontos indicados na
tabela.
A taxa de variação da função f é dada por:
14  5 14  8 k  5
a


.
60
6 m 7 0
Desse modo,
6
3

m2
6m 2

 k  m  17,5.
k  15,5
k 5 3

7
2
10.[C]
O numerador é definido para todo x real tal que x  2  0  x  2. O denominador é definido
para todo x real tal que 3  x  0  x  3. Portanto, Df  {x  | 2  x  3}.
11.[E]
Como f e g são funções crescentes, segue que o valor máximo do quociente
f(4) 3  4 1
f(8) 3  8

 1, e o valor mínimo é

 .
g(9) 4  9 3
g(6) 4  6
f(x)
é
g(y)