Unicamp

Unicamp
ETAPA
QUESTÃO 14
Sejam c um número real e f(x) = x2 − 4x + c uma função quadrática definida para todo número
real x. No plano cartesiano, considere a parábola dada pelo gráfico de y = f(x).
a) Determine c no caso em que a abscissa e a ordenada do vértice da parábola têm soma nula
e esboce o respectivo gráfico para 0 ≤ x ≤ 4.
2
y
1
0
0
1
2
3
4
x
_1
_2
b) Considere os pontos de coordenadas A = (a, f(a)) e B = (b, f(b)), onde a e b são números reais
com a < b. Sabendo que o ponto médio do segmento AB é M = (1, c), determine a e b.
Resposta
2
a) O vértice da parábola dada é e − − 4 , − (− 4) − 4 $ 1$ c o = (2, c – 4). Assim, 2 + c – 4 = 0 +
2 $1
4 $1
+ c = 2.
2
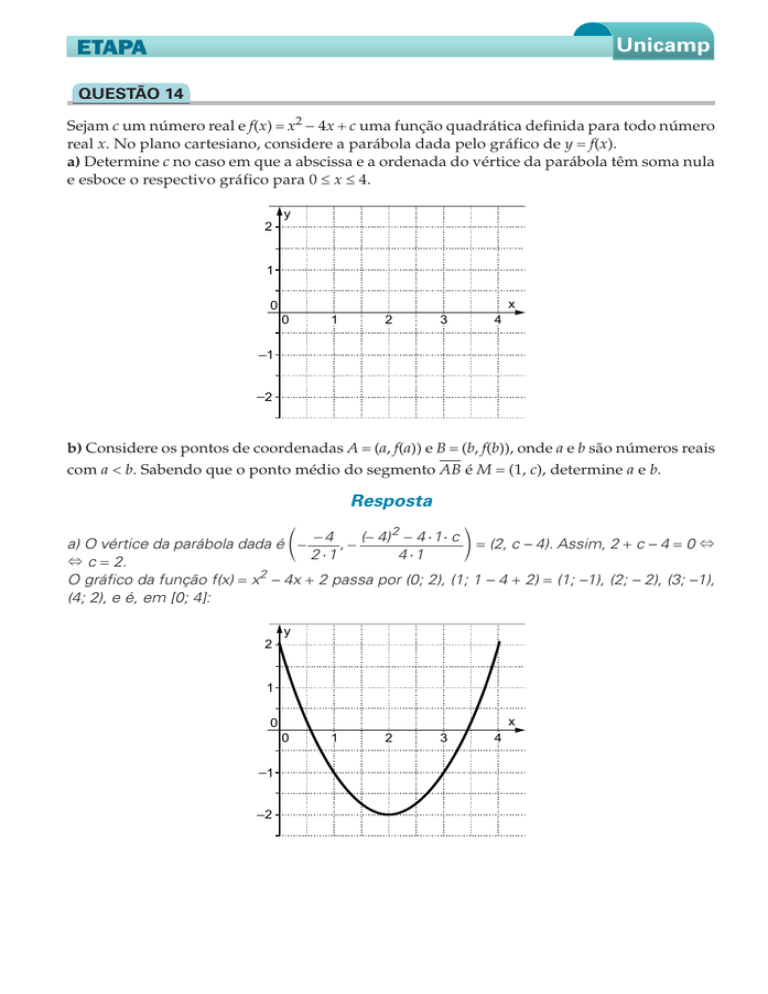
O gráfico da função f(x) = x – 4x + 2 passa por (0; 2), (1; 1 – 4 + 2) = (1; –1), (2; – 2), (3; –1),
(4; 2), e é, em [0; 4]:
2
y
1
0
_1
_2
0
1
2
3
4
x
Unicamp
ETAPA
b) Sendo M o ponto médio de AB, e sendo a < b,
a +b
=1
a +b =2
2
+
+ 2
f (a) + f (b)
a − 4a + c + b 2 − 4b + c = 2c
=c
2
+
b =2 −a
a 2 − 4a + (2 − a) 2 − 4(2 − a) = 0
+
b =2 −a
a 2 − 2a − 2 = 0
+
a =1 − 3
.
b =1 + 3