Universidade de Évora

Engenharia do Ambiente
2º Teste de Mecânica dos Fluidos (1º semestre, 3º ano)
(19 de Dezembro de 2013)
Duração 1h30. Justifique todas as respostas.
Problema I
y
x
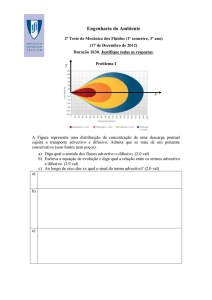
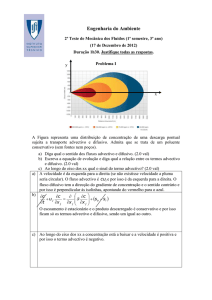
A Figura representa uma distribuição de concentração de uma descarga pontual atmosférica sujeita a
transporte advectivo e difusivo (turbulento). Admita que se trata de um poluente conservativo (sem fontes
nem poços).
a) O transporte pela velocidade (advectivo) faz-se ao longo do eixo xx e o transporte difusivo ao longo
do eixo yy. Qual destes fluxos é o mais importante? Poderia a partir da figura estimar a importância
relativa dos dois fluxos? (2.0 val)
b) Qual a relação entre a divergência dos fluxos advectivo e difusivo? (2.0 val)
c) Se a velocidade do ar baixasse, o que aconteceria à largura da mancha laranja? (2.0 val)
Resolução
a) O fluxo mais importante é o advectivo porque a mancha é muito mais longa na direcção xx do que
na direcção yy. Se o transporte advectivo fosse nulo a mancha seria circular. A importância relativa
dos dois pode ser medida pela razão entre o comprimento de uma isolinha na direcção xx e na
direcção yy (subtraindo 1, porque seriam iguais se existisse só difusão).
b) Se o escoamento for estacionário a concentração num ponto mantém-se. Se o produto for
conservativo o que entra é igual ao que sai e por isso a divergência é nula. Os dois únicos termos da
equação de transporte são o termo advectivo e difusivo, que representam respectivamente as
divergências dos fluxos correspondentes e por isso as divergências desses dois fluxos são simétricas.
c) Se a velocidade do ar baixasse o transporte advectivo perderia importância e a razão entre a
largura da mancha e o seu comprimento teria que aumentar. Por outro lado se a velocidade
baixasse a intensidade de turbulência baixaria e por isso a dispersão baixaria, o que implicaria que
a região com concentração elevada aumentasse de volume.
Problema II
Um carro a deslocar-se à velocidade de 100 km/h precisa de uma potência de 15 kw para vencer a força de
resistência aerodinâmica. De que potência necessitará para vencer a mesma força de resistência quando se se
deslocar a 200 km/h? Que hipótese teve de fazer para resolver o problema? (3 val)
Resolução
As velocidades são elevadas (100km/h = 100000/3600=32m/s) e por isso o Re é elevado. Se a largura
do carro fosse 1.6 m Re seria 5E06. Vamos por isso admitir que o coeficiente de resistência se mantém
constante. Nesse caso a força de resistência aumentará para o quádruplo (é proporcional ao quadrado
da velocidade) e a potência aumentará 8 vezes (é proporcional à força vezes a velocidade e por isso ao
cubo da velocidade). A Potência será por isso de 120 kw.
Problema III
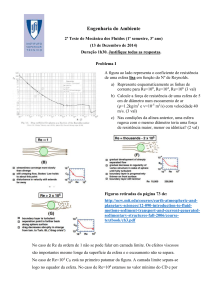
A Figura ao lado representa dois perfis de velocidade numa
camada limite.
a) Para cada um dos perfis desenhe os perfis de tensão
de corte e a divergência do fluxo difusivo (termo
difusivo) (2 valores)
b) Num dos casos o gradiente de pressão é adverso.
Diga em qual. (2 val)
c) O perfil superior corresponde a um escoamento
laminar. Esboce a forma que teria se o escoamento
fosse turbulento. Poderia dizer que a tensão de corte
na parede era superior? (2 val)
Resolução
a) A tensão de corte é o produto da viscosidade pelo gradiente de velocidades. O primeiro perfil não
tem ponto de inflexão e por isso a tensão de corte baixa desde a parede (onde é máxima) até ao
limite da camada limite onde é nula. A divergência do fluxo difusivo é o termo difusivo e será
sempre negativa pois todas as camadas perdem mais quantidade de movimento para a camada de
baixo do que recebem da de cima. Se o perfil de tensão de corte fosse linear, a segunda derivada
seria constante. Como no limite da camada limite a tensão tende assimptoticamente para zero, o
termo difusivo também. A curva deve ser do tipo da curva a vermelho e não da curva a azul (que foi
retirada da internet….)
b) Quando o gradiente de pressão é adverso o perfil de velocidades apresenta um ponto de inflexão
entre a parede e o limite da camada limite e por isso o segundo perfil corresponde a um caso com
gradiente de pressão adverso. Sobre a parede a velocidade é nula e por isso a equação fica só com o
termo de pressão (simétrico do gradiente) e o termo difusivo (2ª derivada da velocidade). Se o
gradiente de pressão for positivo a segunda derivada da velocidade tem que ser positiva. Como na
parte superior da camada limite ela tem que ser negativa isso significa que tem que haver ponto de
inflexão quando o gradiente de pressão é positivo.
c) Se o escoamento fosse turbulento, a difusividade aumentaria e consequentemente o perfil de
velocidade ficaria mais cheio junto à parede (perfil a vermelho).
Problema IV
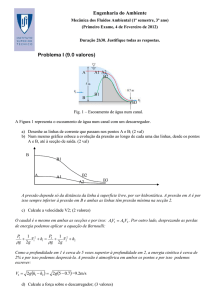
A Figura representa um sifão que despeja um reservatório. Assuma que H
= 5 metros e que o comprimento total do tubo são 15 metros, que a
rugosidade do tubo é 0.3 mm e que o diâmetro são 3 cm.
a) Calcule o caudal escoado se não existisse dissipação de energia. (1
val)
b) Calcule o caudal escoado se o escoamento fosse completamente
rugoso (2 val)
c) Será o escoamento completamente rugoso? (2 val)
Resolução
a) Se não existisse dissipação de energia toda a energia potencial perdida pela água se transformaria
em energia cinética. Aplicando a equação de Bernoulli calcularíamos a velocidade e chegaríamos
a: v  2gH =10m/s e o caudal seria o produto desta velocidade pela área da secção,
Q v *
D2
4
 0.01m3 / s  7L / s
b) Se o escoamento fosse completamente rugoso, o coeficiente de atrito seria independente de Re.
Sendo a rugodidade relativa 0.001, o coeficiente de atrito seria 4f=0.02. A equação de Bernoulli
v
v
L
generalizada seria: H  2g  2g  4f D 
2
10 
2
v2 
15 
1  0.02

2g 
0.03 
2 * 9 .8 * 5
 3m / s
1  10
Q  2.1L / s
V 
c) Para verificar se o escoamento é completamente rugoso tenho que calcular Re e verificar no
diagrama de Moody qual o coeficiente de atrito que corresponde a este Reynolds.
UD 3 * 0.03
Re 

 9 * 10 4 e por isso o escoamento ainda não era completamente rugoso.4f seria 0.022

10  6
e o caudal seria menor do que o calculado. Para o conhecermos deveríamos repetir os cálculos da
alínea b) e fazer um processo iterativo, até que a solução convergisse. Repetindo com 0.022
obteríamos a velocidade de 2.9 e por isso o valor lido no diagrama de Moody já não se alteraria. O
caudal real deve por isso ser ligeiramente inferior ao calculado em b).