Exame 4-Fevereiro2012

Engenharia do Ambiente
Mecânica dos Fluidos Ambiental (1º semestre, 3º ano)
(Primeiro Exame, 4 de Fevereiro de 2012)
Duração 2h30. Justifique todas as respostas.
Problema I (9.0 valores)
A
B
A1 A2
B2
B1
B3
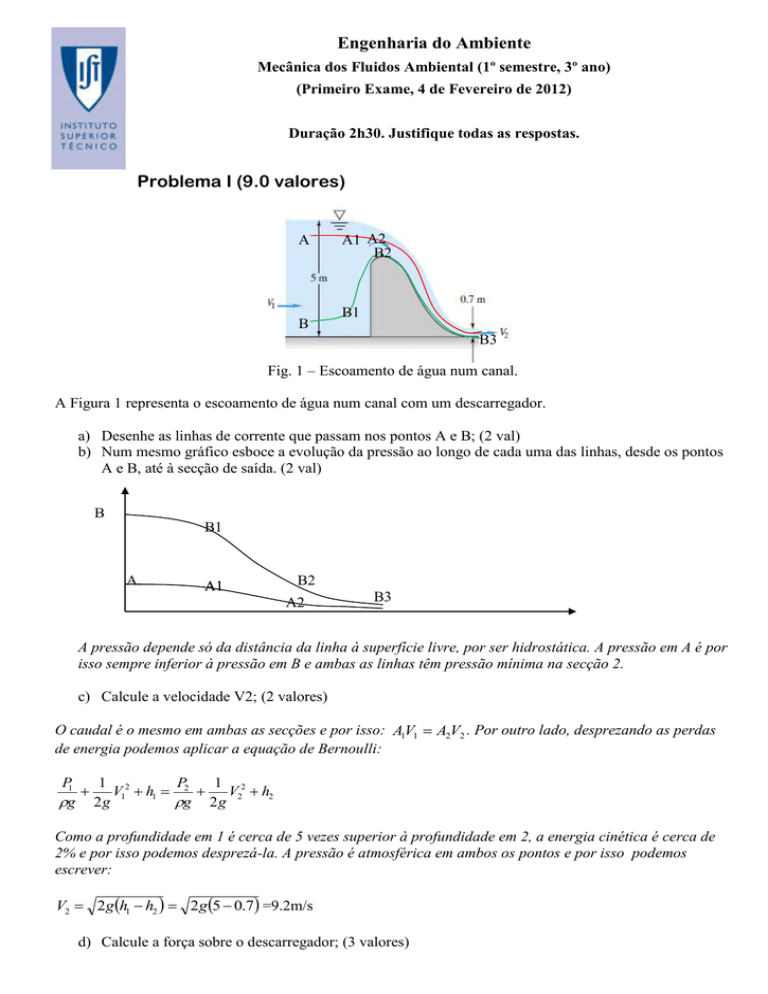
Fig. 1 – Escoamento de água num canal.
A Figura 1 representa o escoamento de água num canal com um descarregador.
a) Desenhe as linhas de corrente que passam nos pontos A e B; (2 val)
b) Num mesmo gráfico esboce a evolução da pressão ao longo de cada uma das linhas, desde os pontos
A e B, até à secção de saída. (2 val)
B
B1
A
A1
B2
A2
B3
A pressão depende só da distância da linha à superfície livre, por ser hidrostática. A pressão em A é por
isso sempre inferior à pressão em B e ambas as linhas têm pressão mínima na secção 2.
c) Calcule a velocidade V2; (2 valores)
O caudal é o mesmo em ambas as secções e por isso: A1V1  A2V2 . Por outro lado, desprezando as perdas
de energia podemos aplicar a equação de Bernoulli:
P1
1 2
P
1 2

V1  h1  2 
V  h2
g 2 g
g 2 g 2
Como a profundidade em 1 é cerca de 5 vezes superior à profundidade em 2, a energia cinética é cerca de
2% e por isso podemos desprezá-la. A pressão é atmosférica em ambos os pontos e por isso podemos
escrever:
V2  2g h1  h2   2g 5  0.7 =9.2m/s
d) Calcule a força sobre o descarregador; (3 valores)
A Força horizontal sobre o descarregador é calculada fazendo um balanço de força e quantidade de
movimento nessa direcção:
 QMS   QME  PAE  PAS  F
1

1

QVS  QVE  h1 *  gh1   h2 *  gh2   F
2

2

A força exercida sobre o fluido são -69400 N/m e a força exercida sobre descarregador é igual e de sinal
contrário.
Problema II (5 valores)
Através do sistema da Figura 2 (tubo liso) escoa-se
água impulsionada por ar pressurizado no interior do
reservatório.
Fig. 2
a) Qual o valor da pressão no reservatório
quando o caudal são 5 m3/hora? (3 valores)
b) Quanto vale a potência dissipada no interior
da conduta? E o fluxo de energia cinética na
saída? (2 valores)
Quando o caudal são 5m3/h, a velocidade no tubo é 0.89 m/s, Re=4.4*105 e do Moody vem 4f=0.021.
Aplicando a equação de Bernoulli considerando exclusivamente as perdas em linha:
P1
1 2
P
1 2
L

V1  h1  2 
V2 1  4 f   h2
g 2 g
g 2 g 
D
P1
1 
L
 h2  h1  
V2 1  4 f 
g
2g 
D
P1
1
170 

 80  10 
8.42 1  0.021
  98m
g
2g
0.05 

P1  9.8atm  9.8kg / cm 2  9.8bar  9.8 * 105 Pa
A potência dissipada é a energia dissipada por unidade de tempo. Por unidade de peso dissipamos
1 
L
P 
V2 1  4 f 
2g 
D
E por unidade de tempo dissipamos esta quantidade vezes o peso que passa por unidade de tempo:
1 
L
Pot 
V2 1  4 f  * gQ  28 *103 * 9.8 * (5 / 3600)
2g 
D
Pot  385w  0.52hp
Problema III (6 valores)
PI
PI
PI
(a)
(b)
(c)
(d)
Fig. 3
A Figura 3 mostra 4 perfis de velocidades em escoamentos do tipo camada-limite. Os 3 da direita têm ponto
de inflexão (PI) e um deles tem tensão de corte nula sobre a parede (perfil (c)).
a) Represente de forma esquemática os perfis de tensão de corte tendo o cuidado de referenciar o ponto
de inflexão (se preferir pode fazer o desenho no enunciado e entregá-lo). Justifique a forma das
curvas. (1.5 valores)
O primeiro perfil não tem ponto de inflexão e por isso a tensão de corte só pode ser máxima na parece. A
tensão tem que variar entre zero no “limite” da camada limite onde o gradiente de velocidade é nulo e o
valor máximo na parede. Nos outros perfis existe ponto de inflexão. Nesse ponto a segunda derivada da
velocidade é nula e a primeira é máxima. Nesses pontos a tensão de corte vai ter um máximo. No caso do
perfil (c) a tensão de corte é nula na parede (é o ponto onde o escoamento se vai separar) e no perfil (d) o
escoamento já está separado, apresentando um ponto de derivada nula da velocidade, onde a tensão de
corte vai ser nula.
b) Na mesma figura indique quais as zonas onde o termo difusivo da equação de Navier-Stokes é
positivo e justifique porquê. (1.5 valores)
O termo difusivo é o simétrico da divergência do fluxo difusivo e por isso é dado pela segunda derivada da
velocidade. Ele é positivo onde a segunda derivada da velocidade é positiva (concavidade do perfil de
velocidades é virada para cima. No primeiro perfil é sempre negativo (todas as camadas do fluido perdem
quantidade de movimento por atrito). Nos outros perfis o sinal muda no ponto de inflexão, é negativo acima
e é positivo abaixo. Isto significa que as camadas de fluido acima do ponto de inflexão são travadas pela
difusão (perdem quantidade de movimento), enquanto que as que estão abaixo do ponto de inflexão ganham
quantidade de movimento por difusão.
c) O perfil (b) corresponde a uma situação de gradiente de pressão positivo. Mais algum dos perfis
corresponde a escoamentos com o mesmo tipo de gradiente? (1.5 valores)
Sim. Todos os perfis que têm ponto de inflexão têm gradiente de pressão positivo (desfavorável). A Equação
de Navier-Stokes:
ui
u
p
 ui
 u j i  


t
x j
xi x j x j
Na parede, onde a velocidade é nula, simplifica-se para:

p
 ui


xi x j x j
E por isso, se o gradiente de pressão é positivo, o termo difusivo tem que ser positivo junto à parede. Como
na parte superior da camada limite a velocidade tem que tender para a velocidade no exterior, a tensão de
corte tem que tender para zero e o perfil tem curvatura negativa, teremos que ter no interiro da camada
limite um ponto de inflexão.
d) Qual o sinal do termo advectivo no interior da camada limite, no caso do perfil (b)? (1.5 valores)
O termo advectivo da equação de Navier-Stokes mede a aceleração de uma partícula de fluido no caso de o
escoamento ser estacionário. Nas zonas onde a velocidade diminui (gradiente longitudinal de velocidade
negativo) o termo convectivo da velocidade é negativo.
Antes da separação da camada limite o termo advectivo é negativo. A velocidade vai a baixar ao longo do
escoamento devido ao gradiente adverso de pressão, até que o fluido acaba por parar (no ponto de
separação). Na zona onde o escoamento está invertido (depois da separação), aplica-se o mesmo raciocínio.
Se pensarmos no módulo da velocidade vemos que ele aumenta para a direita (o gradiente de velocidade é
negativo porque a velocidade é negativa). Como a velocidade é negativa, o termo advectivo é positivo nesta
zona.