Resolucao do 2 teste - 17 de Dezembro de 2012

Engenharia do Ambiente
2º Teste de Mecânica dos Fluidos (1º semestre, 3º ano)
(17 de Dezembro de 2012)
Duração 1h30. Justifique todas as respostas.
y
Problema I
x
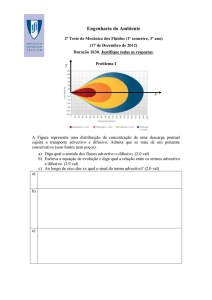
A Figura representa uma distribuição de concentração de uma descarga pontual
sujeita a transporte advectivo e difusivo. Admita que se trata de um poluente
conservativo (sem fontes nem poços).
a) Diga qual o sentido dos fluxos advectivo e difusivo. (2.0 val)
b) Escreva a equação de evolução e diga qual a relação entre os termos advectivo
e difusivo. (2.0 val)
c) Ao longo do eixo dos xx qual o sinal do termo advectivo? (2.0 val)
a) A velocidade é da esquerda para a direita (se não existisse velocidade a pluma
seria circular). O fluxo advectivo é cui e por isso é da esquerda para a direita. O
fluxo difusivo tem a direcção do gradiente de concentração e o sentido contrário e
por isso é perpendicular às isolinhas, apontando do vermelho para o azul.
b) c
c
  c 
 uj


 so  si 
t
x j x j  x j 
O escoamento é estacionário e o produto descarregado é conservativo e por isso
ficam só os termos advectivo e difusivo, sendo um igual ao outro.
c) Ao longo do eixo dos xx a concentração está a baixar e a velocidade é positiva e
por isso o termo advectivo é negativo.
Problema II
Foram feitos dois ensaios para medir a força de arrastamento de uma bola. Num a
velocidade do escoamento era de U =10 m/s e foi medida uma força de 0.3 N e
noutro, com velocidade de 20 m/s foram medidos 1.9 N. Analise a validade dos
ensaios à luz dos seus conhecimentos sobre variação dos coeficientes de resistência
como nº de Reynolds. (3 val)
O coeficiente de resistência diminui com o aumento de Re. No segundo ensaio Re é o
dobro do primeiro uma vez que é a mesma bola (tem o mesmo diâmetro) e a
velocidade é o dobro. O coeficiente de resistência no segundo ensaio não pode ser
superior ao do primeiro.
FR
. A velocidade duplica e por isso a Energia cinética quadruplica. A
cD 
1 U 2 A
2
força de resistência no segundo ensaio tem que ser menor ou igual a 4 vezes a do
primeiro, i.e., menor ou igual a 1.2N e por isso o ensaio não é credível.
Problema III
+
A Figura ao lado representa o escoamento
em torno de uma bola lisa e rugosa com a
mesma velocidade de aproximação. No
caso da bola rugosa a camada limite
separa-se mais tarde.
a) No caso da bola rugosa indique os
pontos de pressão máxima e
mínima. (2 valores)
b) Num dos casos a separação ocorre
em regime laminar. Diga qual
deles. (2 val)
c) O coeficiente de resistência da
bola rugosa é menor. Explique
porquê. (2 val)
a) O ponto de maior pressão é o ponto de entagnação em frente à bola e o de menor
pressão está no “Equador” da bola, no interior da curvatura das linhas de corrente.
b) A camada limite em laminar tem dificuldade em suportar o gradiente de pressão
adverso por a difusividade molecular ser baixa. A jusante do equador da bola a
pressão iria aumentar até ao polo posterior se a camada não se separasse. A
camada limite separa-se e a pressão já não aumenta, mantendo-se em toda a
esteira o valor idêntico ao do “equador”.
c) EM ambos os casos a pressão no equador é semelhante. No entanto, no caso da
bola rugosa a camada limite separa-se mais tarde e por isso a pressão ainda
aumenta até ao ponto de separação e por isso na esteira da bola rugosa a pressão é
maior do que na esteira da lisa. Como consequência o coeficiente de resistência
da bola rugosa é menor do que o da lisa.
Problema IV
B
H=10 m
A Figura representa uma instalação que liga dois depósitos de água. A diferença de
nível entre as superfícies dos fluidos é de 10 m, o diâmetro do tubo são 5 cm, a
rugosidade é 0.2 mm o comprimento do tubo são 50 metros.
a) Calcule a altura de elevação da bomba e a potência fornecida ao fluido quando
a velocidade na conduta é de 1 m/s (considere só perdas por atrito na conduta).
(3 val)
b) Qual a potência que pouparia se na parte final da conduta fosse colocado um
difusor que reduzisse a energia cinética da água para ¼. (2 val)
a) Temos uma conduta com:

0.2
 0.0004
D 50
UD 1 * 0.05
Re 

 5 *104

10 6
4f  0.03

 p

 p

1 2
1 2
1 2  L


U  z   HB  

U  z  
Utubo  4f 

g
2
g

g
2
g
2
g
 D

1

2
1 
50 
HB  10 
1 0.03
  11.5m
2g 
0.05 
Só considerámos perda por atrito no tubo.
b) Na realidade há mais perdas do que as perdas por atrito no tubo. Toda a energia
cinética à entrada do depósito superior (Energia cinética no tubo) se dissipa por
turbulência no interior do reservatório. Se a potência perdida fosse significativa,
poderia ser interessante recuperá-la instalando um difusor. Se esse difusor
reduzisse a velocidade para metade a energia dissipada seria ¼ e por isso
pouparíamos ¾ da energia. A Potência seria o produto da energia por unidade de
volume poupada pelo volume por unidade de tempo (caudal volúmico)
2
31
31

 0.05
Pot   U 2 Q   1000 *1(
*1)  0.74w
42
42
4


A potência poupada seria desprezável (menos de 1 watt). Na realidade só vale a
pena pensar nessa energia quando o caudal é muito elevado (da ordem dos m3/s).
é por isso que faz sentido em condutas compridas pensar só nas perdas por atrito
na conduta.