Teste 2_2014_2015(Resolução)

Engenharia do Ambiente
2º Teste de Mecânica dos Fluidos (1º semestre, 3º ano)
(13 de Dezembro de 2014)
Duração 1h30. Justifique todas as respostas.
Problema I
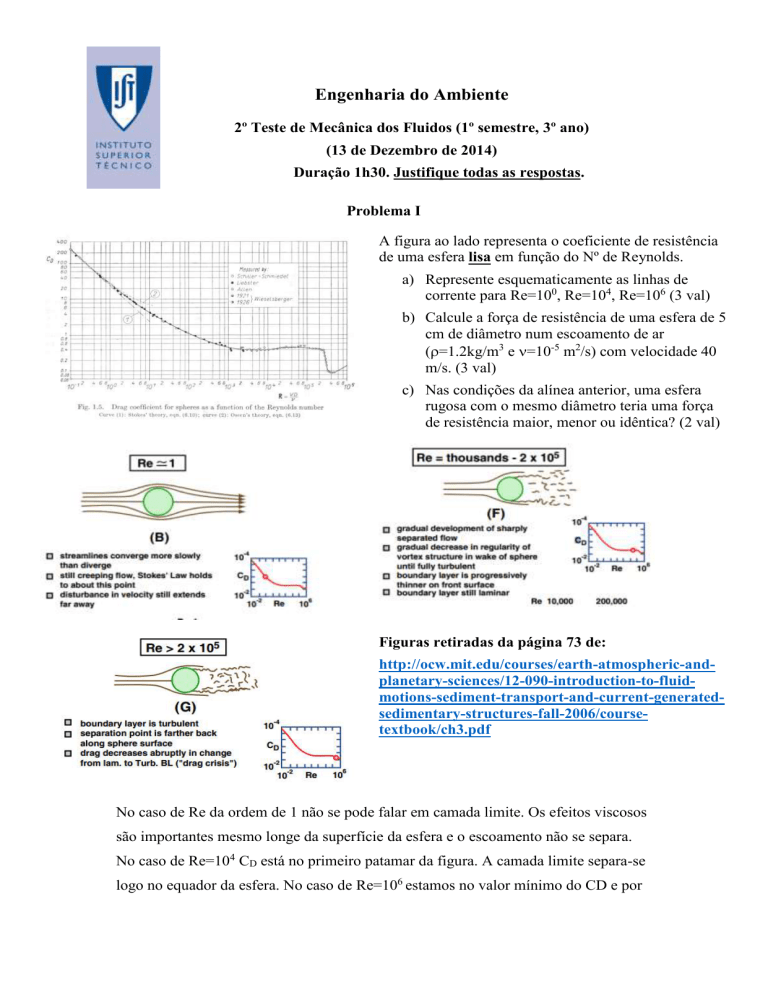
A figura ao lado representa o coeficiente de resistência
de uma esfera lisa em função do Nº de Reynolds.
a) Represente esquematicamente as linhas de
corrente para Re=100, Re=104, Re=106 (3 val)
b) Calcule a força de resistência de uma esfera de 5
cm de diâmetro num escoamento de ar
(=1.2kg/m3 e =10-5 m2/s) com velocidade 40
m/s. (3 val)
c) Nas condições da alínea anterior, uma esfera
rugosa com o mesmo diâmetro teria uma força
de resistência maior, menor ou idêntica? (2 val)
Figuras retiradas da página 73 de:
http://ocw.mit.edu/courses/earth-atmospheric-andplanetary-sciences/12-090-introduction-to-fluidmotions-sediment-transport-and-current-generatedsedimentary-structures-fall-2006/coursetextbook/ch3.pdf
No caso de Re da ordem de 1 não se pode falar em camada limite. Os efeitos viscosos
são importantes mesmo longe da superfície da esfera e o escoamento não se separa.
No caso de Re=104 CD está no primeiro patamar da figura. A camada limite separa-se
logo no equador da esfera. No caso de Re=106 estamos no valor mínimo do CD e por
isso a camada limite tem que separar depois do equador da esfera, originando uma
esteira mais estreita.
A Força de Resistência é dada por:
FR  CD
1
U 2 A
2
O valor de CD depende de Re:
40 * 0.05
 2 * 105
5

10
CD  0.4
Re 
UD

1
0.052
2
FR  0.4 1.2 * 40 * 
 0.75N
2
4
Problema II
A
B
C
A figura representa um escoamento
estacionário num venturi (contração
seguida de expansão). A linha a
tracejado pretende representar a
camada limite.
Escreva a equação de Navier
Stokes para os pontos A, B e C,
eliminando os termos desprezáveis
em cada um deles (advecção,
pressão e difusão)? (4 val)
A Equação de Navier-Stokes na sua forma geral é:
dui
ui
p

u

 u j
 

 i  gi
dt
x j
xi
x j x j
No Ponto A estamos fora da camada limite e por isso os efeitos viscosos são nulos. O
escoamento tem aceleração positiva e por isso o gradiente de pressão é negativo. O
escoamento é estacionário e horizontal e por isso a aceleração convectiva é equilibrada (é
devida) ao gradiente de pressão. A equação resume-se a:
ui
p
 
x j
xi
O ponto B está dentro da camada limite, numa região onde esta ainda não separou e onde o
gradiente é adverso. Neste caso todos os termos da equação de Navier-Stokes são importantes,
mas a componente de velocidade importante é segundo x1 e a difusão é importante segundo
x2. A equação pode por isso simplificar-se para:
u j
u1
p

u
 

 1
x j
x1
x2 x2
O ponto C está na região onde a camada limite já se separou e por isso onde o gradiente de
pressão é desprezável. A equação pode simplificar-se para:
u j
u j
u1

u

 1
x j
x 2 x 2
Problema III
Para o caso da figura ao lado, para =60º e rugosidade
do tubo de 0.5 mm, calcule:
a)
b)
c)
d)
O caudal escoado no caso de fluido ideal (1 val)
O valor de h (1 val)
O caudal escoado no caso de fluido real (2 val)
A altura de elevação da bomba a instalar, no
caso de se pretender o dobro do caudal (2 val)
e) Explique porque motivo as curvas do coeficiente
de atrito tendem a tornar-se independentes de
Re, quando este é elevado (2val)
No caso de fluido ideal pode ser aplicada a equação de Bernoulli. A Energia
cinética na saída do tuo resulta da conversão da energia potencial na superfície do
reservatório. A cota de saída é dada por:
z2  L sin  5 * sin 60  4.33m
A Equação de Bernoulli dá:
1 2
1 2
U1  z1 
U2  z 2
2g
2g
0  10 
1 2
U2  4.33
2g
U2  10.64m / s
Q  U2 * 
D2
0.032
 10.64 * 
 7.5L / s
4
4
A altura a que o jato subiria depende da conversão de energia cinética em energia
potencial. Se o jato fosse vertical essa conversão seria total e h seria nulo. Neste
caso só a componente vertical da velocidade será convertida e por isso h é nãonulo.
A componente vertical da velocidade é:
Uv  U sin  10.64 * sin 60  9.21m / s
UH  U cos   10.64 * cos 60  5.32m / s
A energia cinética perdida na subida corresponde à componente vertical da
velocidade. A componente horizontal mantém-se.
Aplicando a equação de Bernoulli obtém-se:
1 2
1 2
U1  z1 
U2  z 2
2g
2g
10.64 2
5.32
 4.33 
 z2
2g
2g
z 2  4.33  5.62  1.41  8.53m
h  10  8.53  1.47m
Para calcular o caudal no caso de fluido real, teremos que calcular as perdas de
energia por atrito. Para isso teremos que conhecer o coeficiente de atrito, função
de Re e da rugosidade relativa. Como não conhecemos a velocidade vamos
começar por verificar se em condições ideais a velocidade é suficiente para termos
escoamento completamente rugoso.
r 
Re 


D
UD

0.5
 0.017
30

10.64 * 0.03
 3 * 105
10 6
4f  0.047
Com a velocidade calculada n caso de escoamento ideal o escoamento já seria
completamente rugoso e por isso vamos iniciar um processo iterativo com esta
velocidade.
1 2
1 2
1 2
L
U1  z1 
U2  z 2
UTubo 4f
2g
2g
2g
D
0  10  4.33 
U2 
1 2
5 
U2 1  0.047 *

2g
0.03 

10  4.33
1
5 

* 1  0.047 *

2g 
0.03 

5.67
 3.58m / s
0.441
O novo Reé 1/3 do inicial (105) e o escomento é efectivamente completamente
rugoso e por isso a velocidsade está bem calculada. O cauldal seré cerca de 1/3 do
ideal (2.5 L/s)
Se pretender o dobro do caudal o escoaento continua a ser completamente rugoso
e por isso o coeficiente de atrito é o da alínea anterior. Neste caso a equação de
Bernoulli seria:
1 2
1 2
1 2
L
U1  z1  H 
U2  z 2
UTubo 4f
2g
2g
2g
D
0  10  H  4.33 
1
5 

7.16 2 1  0.047 *

2g
0.03 

H  4.33  10  10.4  4.7m
As curvas do coeficiente de atrito tendem para valores constantes para valores de
Re elevados porque as tensões de corte de origem turbulenta dominam o
escoamento.
f 
w
1
U 2
2

 vis c   turb
1
U 2
2


U
U
 u'i u'j
  U 2

1
D
 D

 C te 
 C te
1
1
UD
Re
U 2
U 2
2
2
O inverso de Re tende para zero quando este aumenta.