Teste 1_2011_2012

Engenharia do Ambiente
Mecânica dos Fluidos Ambiental (1º semestre, 3º ano)
(Primeiro Teste, 18 de Novembro de 2011)
Duração 1.5 horas. Justifique todas as respostas.
Consulta: Formulário com 2 páginas.
Problema I
r
A
x
B
h
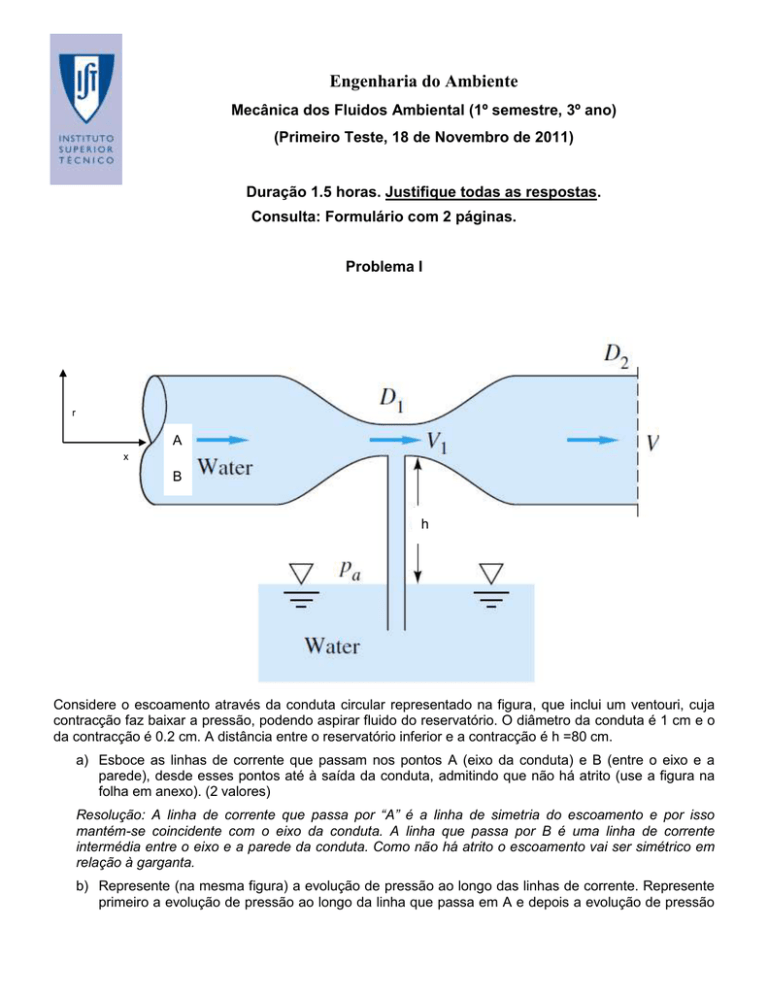
Considere o escoamento através da conduta circular representado na figura, que inclui um ventouri, cuja
contracção faz baixar a pressão, podendo aspirar fluido do reservatório. O diâmetro da conduta é 1 cm e o
da contracção é 0.2 cm. A distância entre o reservatório inferior e a contracção é h =80 cm.
a) Esboce as linhas de corrente que passam nos pontos A (eixo da conduta) e B (entre o eixo e a
parede), desde esses pontos até à saída da conduta, admitindo que não há atrito (use a figura na
folha em anexo). (2 valores)
Resolução: A linha de corrente que passa por “A” é a linha de simetria do escoamento e por isso
mantém-se coincidente com o eixo da conduta. A linha que passa por B é uma linha de corrente
intermédia entre o eixo e a parede da conduta. Como não há atrito o escoamento vai ser simétrico em
relação à garganta.
b) Represente (na mesma figura) a evolução de pressão ao longo das linhas de corrente. Represente
primeiro a evolução de pressão ao longo da linha que passa em A e depois a evolução de pressão
ao longo da linha que passa em B, tendo o cuidado de indicar as zonas onde as pressões são
diferentes. (2 valores)
Resposta: a pressão vai diminuir na zona onde a velocidade aumenta (aceleração positiva requer força
no sentido do escoamento) e aumentar na zona onde a velocidade diminui pois nesta zona a força é no
sentido contrário do escoamento. Qualitativamente o andamento é semelhante nas duas linhas de
corrente. Nas zonas onde há curvatura das linhas de corrente há força centrífuga e por isso, na entrada
da contracção a pressão do lado da parede é maior do que no eixo e na garganta a pressão é maior no
eixo porque este está do lado de fora da curva.
c) Quanto vale a pressão na garganta do ventouri quando a água sobe no tubo vertical até à garganta,
mas ainda não há caudal no tubo? (1 valores)
1
1

 

2
2
 P  gu  gz    P  gu  gz 
2
2

1 
2
PG  PR  g z R  zG   gh  0.8 * 10 4 Pa
d) Se a pressão na secção dos pontos A e B fosse 120 cm de coluna de água
( p  g *1.2  103 * 9.8 *1.2  103 Nm2  1.2 *10 4 Pa ) quanto valeria o caudal nas condições da
alínea anterior? (3 valores)
1
1

 

2
2
 P  gu  gz    P  gu  gz 
2
2

1 
2
uA1  uA2
1
1
1.2 *10 4  gu12  0.8 *10 4  gu 22
2
2
2
2
0.01
0.002
u1
 u 2
 u1  u 2 * 4 *10 2
4
4
1
1
1.2 *10 4  10 3 * 9.8 * u 22 *16 *10 4  0.8 *10 4  10 3 * 9.8u 22
2
2
1

 2  2 *10 4 
2 *10 4

   2 3

u2   2 3


10
*
9
.
8
1

0
.
0016
10
*
9
.
8




2
0.002
Q  uA2  2 * 
 6.28 *10 6 m 3 / s
4
u1  6.4 *10 2 m / s *
1
2
 4  2m / s
e) Calcule a força que o escoamento exerce sobre as paredes da convergência no caso de não existir
atrito (se não resolveu a alínea anterior admita que a velocidade na garganta é 10 m/s. Nessas
condições quanto vale a força exercida em todo o ventouri (contracção + expansão)? (3 valores)
uQ 2  uQ 1  PA1  PA2  F
6
2
10 * 2 * 6.28 *10  10 * 6.4 *10 * 6.28 *10
3
3
6
0.012
0.002 2
4
 1.2 *10 *  *
 0.8 *10 *  *
F
4
4
4
F  12.1*10 3  0.93  2.4 *10 2  0.93N
E a força exercida pelo fluido sobre a contração tem o mesmo valor absoluto e sinal contrário.
f)
Na realidade existe atrito nas paredes da conduta. Esboce o perfil de velocidades e de tensão de
corte na secção dos pontos AB e esboce a evolução da tensão de corte NA PAREDE entre esta
secção e a garganta do ventouri (pode usar a figura em anexo). Qual o sentido do fluxo difusivo?
Qual o sinal da divergência do fluxo difusivo? (3 valores)
O Fluxo difusivo é do eixo do tubo para a parede e a divergência é positiva. Sai mais em (r+dr) do que entra
em r.
Problema II
Comente as seguintes afirmações, dizendo se são verdadeiras ou falsas:
g) A viscosidade de um gás depende da velocidade do movimento browniano das moléculas. (2
valores)
Verdade. A viscosidade é a constante de proporcionalidade entre o gradiente e o fluxo difusivo, o qual
quantifica o transporte associado aos movimentos não descritos pela velocidade. No caso do escoamento
laminar o movimento não descrito é o browniano.
h) A aceleração de uma porção de fluido é nula num escoamento estacionário. (2 valores)
Não verdadeira. A aceleração de uma porção de fluido é a aceleração local temporal mais a aceleração
convectiva. A local é que é nula nos escoamentos estacionários.
i)
O fluxo difusivo é perpendicular às isolinhas de concentração e directamente proporcional à
distância entre elas. (2 valores)
Parcialmente verdadeira. O fluxo difusivo é devido ao gradiente e por isso é perpendicular às isolinhas. No
entanto, por ser proporcional ao gradiente é inversamente proporcional à distância entre as isolinhas.
A
B
h

P,
A
B

x