Resolução do Teste de Novembro de 2009

Engenharia do Ambiente
Mecânica dos Fluidos Ambiental (1º semestre, 3º ano)
(Primeiro Teste, 17 de Novembro de 2009)
Duração 1.5 horas. Justifique todas as respostas.
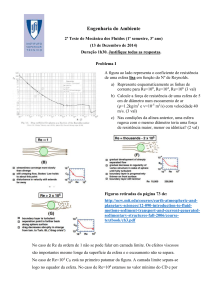
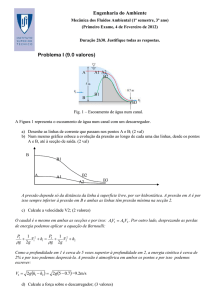
VC
X2
F
X1
Representação esquemática de um escoamento estacionário com superfície livre sobre uma sobreelevação do fundo. “F” representa a força exercida pelo ressalto sobre o escoamento. “VC” representa um
volume de controlo.
a) Explique porque baixa a superfície livre sobre o ressalto. Calcule a velocidade V 1 e o caudal (por
unidade de largura) admitindo que a velocidade é uniforme na coluna de água. (3 val).
Res: A superfície livre sobre o ressalto baixa por conservação da energia mecânica. A sobre-elevação faz
diminuir a área de passagem e por isso aumentar a velocidade. O aumento de velocidade tem associado o
aumento de energia cinética e por isso outra forma de energia tem que baixar (pressão ou energia
potencial). Na superfície livre a pressão é atmosférica e não pode variar. Só a energia potencial é que pode
baixar. A velocidade pode ser calculada aplicando a equação de Bernoulli entre um ponto à superfície
antes do ressalto (cota = 2 metros) e o ponto sobre o ressalto, também à superfície onde a cota é 1.9
metros e a pressão é também atmosférica. A equação tem duas incógnitas e por isso precisamos de mais
uma equação: Balanço de massa. O caudal é igual nas duas secções, sendo numa a área de passagem de
2 m2 e na outra (2-0.1-0.4=1.6m2). A resolução do sistema de equações dá a velocidade em ambas as
secções, tal como no caso do tubo de Ventouri que fizemos nas aulas. [NOTA: verão em Hidráulica que no
caso de o nº de Froude antes da sobre da sobre-elevação ser superior a 1, tudo seria ao contrário, o nível
aumentaria em cima da sobre-elevação e a energia cinética teria que baixar. Isto pode acontecer porque a
equação da energia é quadrática e por isso pode ter duas soluções].
b) Calcule os fluxos de quantidade de movimento na secção antes da sobre-elevação e sobre a sobreelevação. (2 val).
Res: Os fluxos de quantidade de movimento são dados pelo integral na área da quantidade de movimento
por unidade de volume pelo volume por unidade de tempo. Se a quantidade de movimento por unidade de
volume for uniforme na área pode sair do integral e o fluxo é dado por (ρVQ). No caso deste problema
temos que fazer esta hipótese e por isso os fluxos calculam-se algebricamente.
c) Calcule a componente horizontal da força F exercida pelo ressalto sobre o escoamento. Como
poderia calcular a componente vertical? (3 val).
Res: A força calcula-se fazendo um balanço de “força e variação do fluxo de quantidade de movimento”.
A alínea anterior mostra que o fluxo de quantidade de movimento é maior sobre o ressalto (a velocidade
aumenta e o caudal mantém-se) e por isso a resultante das forças é no sentido do ressalto. Ignorando o
atrito (não temos a tensão de corte sobre o fundo) as forças são de pressão e a força no ressalto (que é
negativa). A força de pressão é hidrostática e por isso é dada pela pressão no centro de gravidade
(meia profundidade) vezes a área. A força sobre o ressalto é a única incógnita. A componente vertical
(na hipótese hidrostática) é o peso do fluido. Para calcular teríamos que conhecer a forma da superfície
livre, que poderia ser calculada usando a equação de Bernoulli, se conhecêssemos a forma do
obstáculo.
d) Efectivamente a pressão sobre o ressalto não é hidrostática. Desenhe uma linha de corrente na
face anterior do obstáculo e indique o ponto de pressão máxima. Explique os processos que
determinam a variação vertical da pressão no topo do ressalto. (3 val).
Res:A linha de corrente é mais ou menos paralela ao fundo. Isso significa que no início do obstáculo tem
curvatura virada para cima e sobre o obstáculo tem curvatura virada para baixo. Antes do obstáculo a
pressão no fundo são 2 metros. Quando o fluido que está perto do fundo se aproxima do obstáculo fica
sujeito a uma trajectória com curvatura e por isso a pressão aumenta no fundo devido à força centrífuga.
O ponto de pressão máxima é por isso nessa zona e a pressão é superior à hidrostática. À medida que o
fluido se aproxima do topo do obstáculo a pressão hidrostática baixa, mas a pressão tem ainda uma
redução adicional devido à curvatura das linhas de corrente que contribui neste caso para a redução da
pressão junto ao fundo por a curvatura ser ao contrário da curvatura na zona de aproximação.
e) Efectivamente a velocidade não é uniforme na vertical. Esboce os perfis verticais de velocidade e de
tensão de corte antes e sobre o ressalto. Tenha em atenção o gradiente horizontal e vertical de
velocidade e diga onde é máxima a tensão de corte. Diga também onde se dissipa a energia
mecânica e onde é máxima a taxa de dissipação. (3 val).
Res:Os perfis de velocidade são do tipo parabólico se o escoamento for laminar ou logarítmico se for
turbulento. Em qualquer dos casos a velocidade será nula junto ao fundo e será junto ao fundo que o
gradiente de velocidades será máximo e por isso a tensão de corte será máxima. À superfície a tensão
de corte será nula. Se admitirmos pressão hidrostática o gradiente de pressão só vai depender da
inclinação da superfície livre e por isso não depende da profundidade. Como consequência, antes do
obstáculo a tensão de corte tem um perfil linear. Sobre o obstáculo o gradiente de pressão seria
também independente da profundidade, mas o termo advectivo é diferente de zero e por isso a tensão
de corte não tem que ter um perfil linear.
A dissipação de energia é proporcional ao quadrado do gradiente de velocidade e por isso existe em
todos os pontos onde existe gradiente de velocidade (e tensão de corte). Vai ser máxima no fundo.
f)
Escreva a equação de transporte de quantidade de movimento para a componente horizontal da
velocidade. Para o volume de controlo “VC” diga qual o sinal do termo convectivo na direcção
horizontal. (3 val).
Res: A equação de transporte de quantidade de movimento obtém-se da equação de Navier Stokes
eliminando a derivada temporal (o escoamento é estacionário). Os outros termos dependem da zona
onde estamos. Antes do ressalto o perfil está completamente desenvolvido (desprezando o atrito) e por
isso o termo convectivo é nulo (não há aceleração). Fica só equilíbrio entre o gradiente de pressão e a
difusão vertical como no caso do filme líquido. Sobre o ressalto temos aceleração e velocidade vertical,
pelo que temos termo advectivo na horizontal e na vertical (embora o termo horizontal deva ser mais
importante) e temos também difusão vertical. O volume de controlo está nesta segunda zona. O termo
convectivo é positivo porque a aceleração é positiva.
g) Para o mesmo volume diga qual o sinal do fluxo difusivo vertical de quantidade de movimento e qual
o sinal do termo difusivo da equação de Navier-Stokes. Qual o fluxo difusivo mais importante: o
vertical ou o horizontal? (3 val).
Res: O fluxo difusivo é a tensão de corte. Ele é perpendicular à velocidade e no sentido contrário ao
gradiente. Neste acaso a componente mais importante do gradiente de velocidade é a vertical e por
isso o fluxo difusivo é essencialmente vertical e é no sentido descendente porque é nesse sentido que a
velocidade baixa. O termo difusivo das equações é a divergência do fluxo difusivo. Como a tensão de
corte na parte de cima do volume é menos do que na parte de baixo, o volume perde quantidade de
movimento por difusão. O termo difusivo é por isso negativo. Também se poderia chegar a esta
conclusão pela concavidade do perfil de velocidades, mas seria menos interessante do ponto de vista
dos conceitos de MFA.