questões de vestibulares

QUESTÕES DE VESTIBULARES
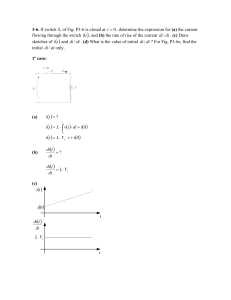
01- (FATEC) Na figura abaixo tem-se o ponto P, afixo do número complexo z, no plano de Argand-Gauss.
Se z é o complexo conjugado de z, então
a) z = – 2 + 2 3 i
b) z = – 2 + 2 3 i
c) z = – 2 +
3i
d) z = – 2 +
2 3
i
3
e) z = – 2 +
3
i
3
02- (FATEC_002) Sabe-se que os números z1 = log(x – y) + (y + 10)i e z2 = y – x i, nos quais x e y são números reais,
são complexos conjugados. É verdade que
a) z1 + z2 = 1
b) z1 – z2 = i
c) z1 . z2 = 122
d) |z1 + z2| = 2
e) |z1 – z2| = 11
iu  (1  i) v  i
então:
u  iv  1  i
03- (Fatec-SP) Seja i 2 = 1. Se o par (u, v) de números complexos é solução do sistema 
a) u + v = i.
b) u  v = 1 + i.
c) uv = 1.
d) uv = 1
e) uv = 1 + i
04- (Fatec-SP_002) Seja i tal que i 2 = 1. se z = c + di, com c e d reais, é um número complexo e z o conjugado
de z, então:
a) z  z = 2d
b) z z = c2 – d 2
c) z z = c2 + d 2
d) z .
1
=1
z
e) z z = d 2 – c2
05- (Fatec-SP_003) Seja i 2 = 1 e z o conjugado do número complexo z tal que iz + 2 z + 1 – i = 0. Então:
a) z = 1 + i
b) z = 1 + i
c) z = 1  i
d) z = 1  i
e) z = 0
06- (Osec-SP) Determinando-se os valores reais de m e n de modo que se tenha 2 (m  ni) + i (m + ni)  i = 0, a soma m
+ n vale:
a) – 1
b) 0
c) 1
d) 2
e) 3
07- (UCMG) O número complexo 2z, tal que 5z +
a) 4 + 3i
b) -4 + 3i
c) 4 - 3i
d) -4 - 3i
e) nda
= 12 + 6i é:
08- (UFU-MG) Sejam os complexos z = 2x – 3i e t = 2 + yi, onde x e y são números reais. Se z = t, então o
produto x.y é
A) 6
B) 4
C) 3
D) –3
E) –6
09- (UFV) Seja a equação Z –
satisfazem essa equação é:
a) 2
b) 2i
c) 0
d) 1
e) i
+Z
= 2 + 2i, no conjunto dos números complexos. A soma dos dois números que
10- (UNIFESP) Os números complexos z1, z2 = 2i e z3 = a 3 +ai , onde a é um número real positivo, representam no
plano complexo vértices de um triângulo eqüilátero. Dado que |z 1 – z2| = 2, o valor de a é:
a) 2.
b) 1.
c)
3.
3
.
2
1
e) .
2
d)
11- (Cescem-SP) Seja o número complexo z = (m + 2i)(2 – i), onde m  R. para um determinado valor de m, o número
z pode ser um imaginário puro igual a:
a) 4i
b) i
c) 2i
d) 3i
e) 5i
12- (FAFI-BH) Sendo a = 3 + 2i e b = 5  4i, então a alternativa FALSA sobre os números complexos é:
a) ab = 23  2i
b) a2 = 5 + 12i
c) b2 = 9  40i
d) ai = 2 + 3i
e) a + b = 8  2i
13- (PUC-SP) Qual deve ser o valor de k  R de modo que o número complexo Z =
a) k = 12
b) k = 12
c) k = 14
d) k = 14
e) nda
14- (PUC-SP) O conjugado do número complexo
a)
b)
c)
d)
e)
1  3i
é:
2i
1 7i
5
1 i
5
1 2i
7
1 7i
5
1 i
5
15- (PUC-MG) Qual é o quociente de (8 + i)/(2 - i) é igual a
A) 1 + 2i
B) 2 + i
C) 2 + 2i
D) 2 + 3i
E) 3 + 2i
16- (Santa Casa-SP) O valor de
2i
é igual a:
2i
3 4
 i
5 5
b) 3 - 4i
c) 4 + 3i
2 4
d)  i
3 3
3 4
e)  i
5 5
a)
17- (UFAM_001) A forma a + bi de z = (2 – 2i)/(1 + i) de é:
a) -2i
b) 2i
c) 1 + i
d) 1 – i
e) 2 + 2i
 1  3i
seja real?
4  ki
2
z
18- (UFJF_001) Se z = 2 + 4i e w = 1  i são números complexos, então   é igual a:
w


a) 8  6i
b) 1 +3i
c) 1 + 9i
d) 8 + 6i
e) 8  6i
19- (UFPA) A divisão
1  2i
dá como resultado o número:
1 i
1 3
 i
2 2
1 3
b)  i
2 2
1 3
c)   i
2 2
1 3
d)  i ]
2 2
a) 
e) 1 + 3i
20- (UFPA_002) O quociente de z = 3 + 2i por w = 1 + i é:
a) 3 + 2i
b) 3 – i
c) 5 – i
5 1
 i
2 2
3
i
e)
2
d)
21- (Fasp) Simplificando a expressão 3i5 + 2i4 + 5i3 obtém-se:
a) 2 - 2i
b) 1+ i
c) 2 + 8i
d) 3  3i
e) 2  i
22- (FATEC) Se i é a unidade imaginária, a soma 2 + 4 . i2 + 6 . i4 + ... + 100 . i98 é um número
a) primo.
b) divisível por 4.
c) múltiplo de 6.
d) negativo.
e) quadrado perfeito.
23- (F. C. Chagas) Se i é a unidade imaginária, então
a) –1
b) – i
c) 1 + i
1 i
d)  
2 2
1 i
e)  
2 2
i15  i16
i17  i18
é igual a:
24- (MACK-SP) Calcule o valor da expressão y = i . i 2 . i3 . i4 . ... . i1000.
a) 1
b) i
c) – i
d) – 1
e) 1 + i
25- (Mack-SP) O valor da expressão y = i + i2 + i3 + i4 + i5 + ... + il 00l é:
a) 1
b) i
c) – i
d) – 1
e) 1 + i
26- (MACK) Seja o número complexo Z = i + i2 + i3 + i4 + .... + i1995, onde i =
a) 1 + i
b) i
c) 1
d) i
e) 1
27- (MACK-SP) Se z =
a)
b)
c)
d)
e)
1 i
, então z 1980 é igual a:
1 i
1.
1.
i.
i.
2i.
28- (MACK-SP) Simplificando:
a)
b)
c)
d)
e)
1 . Desta forma Z . Z vale:
(2  i)101 (2  i) 50
, temos:
(2  i)100 (i  2) 49
1
2+i
2–i
5
5
29- (MACK_009) Se k = i1 + i2 + … + in, i2 = – 1, e se n é o número binomial
a) 1
b) –1
c) –1 + i
d) i
e) 0
30- (MACK_008) Se i2 = – 1, o complexo z =
a) da forma a + bi, com a + b = 1.
b)
c)
d)
e)
um número de módulo
um imaginário puro.
um número real.
um número de módulo 1.
2
i 203  i
é:
i 1
9
  , então k é igual a
 4