Exp_6CEE_La_o_Histerese_correguido

CEE – CONVERSÃO ELETROMECÂNICA DE ENERGIA
LAÇO DE HISTERESE
1. TEORIA
Conside uma bobina enrolada em torno de um núcleo magnético. Se na bobina circular uma
corrente alternada, a relação entre a densidade de fluxo magnético B e o campo H, ambos
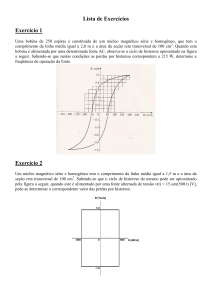
confinados ao núcleo, é descrita pela característica da Fig. 1. Na ilustração, H é o campo
produzido pela corrente da bobina. Essa característica é denominada laço de histerese.
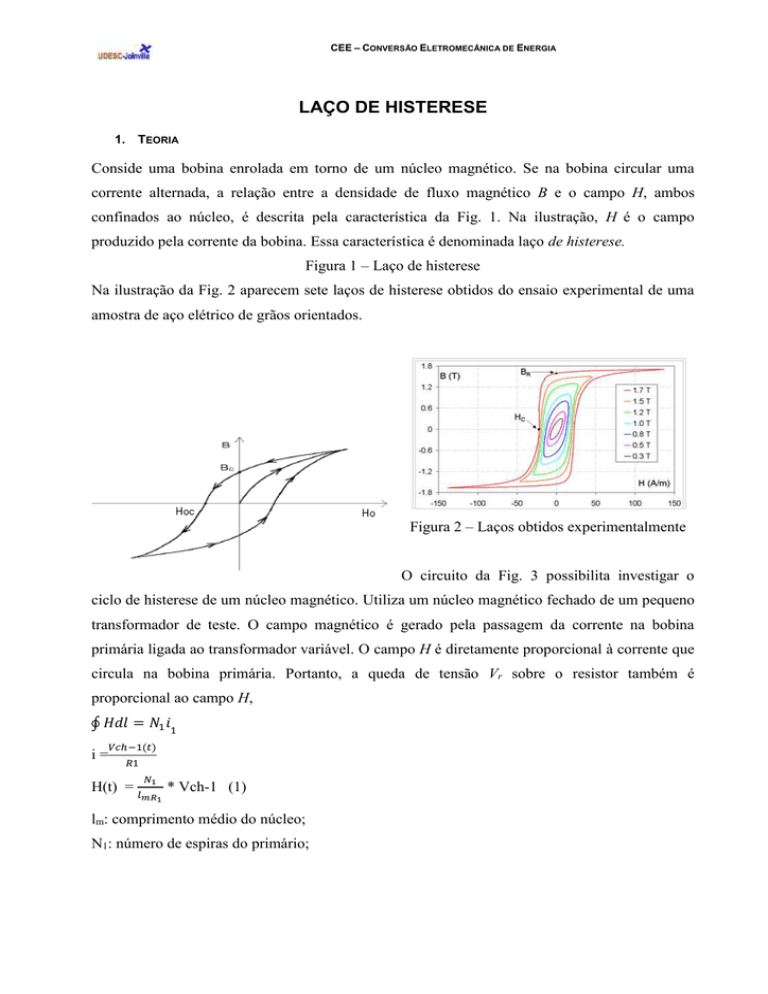
Figura 1 – Laço de histerese
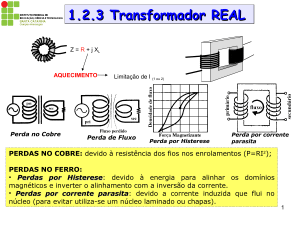
Na ilustração da Fig. 2 aparecem sete laços de histerese obtidos do ensaio experimental de uma
amostra de aço elétrico de grãos orientados.
Figura 2 – Laços obtidos experimentalmente
O circuito da Fig. 3 possibilita investigar o
ciclo de histerese de um núcleo magnético. Utiliza um núcleo magnético fechado de um pequeno
transformador de teste. O campo magnético é gerado pela passagem da corrente na bobina
primária ligada ao transformador variável. O campo H é diretamente proporcional à corrente que
circula na bobina primária. Portanto, a queda de tensão Vr sobre o resistor também é
proporcional ao campo H,
∮ 𝐻𝑑𝑙 = 𝑁1 𝑖1
𝑉𝑐ℎ−1(𝑡)
i=
𝑅1
H(t) = 𝑙
𝑁1
𝑚𝑅1
* Vch-1 (1)
lm: comprimento médio do núcleo;
N1: número de espiras do primário;
CEE – CONVERSÃO ELETROMECÂNICA DE ENERGIA
Figura 3 – Montagem
De acordo com a lei de Faraday, a tensão VS na bobina secundária é diretamente proporcional à
derivada do fluxo total em relação ao tempo. Empregando-se um circuito RC para integrar o
sinal VS tem-se:
Da lei de Faraday
V2 = N2
𝑑𝛷(𝑡)
𝑑𝑡
(2)
Admitindo que a queda vai ser no resistor de um 100KΩ
V2 = ic(t)R2
(3)
lembrando que:
𝑑𝑉𝑐(𝑡)
ic(t) = C
C
𝑑𝑉𝑐(𝑡)
𝑑𝑡
B(t)
𝑑𝑡
(4)
𝑑𝛷(𝑡)
R2 = N2
𝑅
𝑑𝑡
=𝑁 2𝐶𝐴*Vch-2
2
/∫ 𝑑𝑡 (5) , como
ϕ= B(t)* A e Vc(t) = Vch-2
(6)
A: área transversal do núcleo;
N2: número de espiras do secundário;
No caso, Vr(t) é proporcional a H (t) e VC (t) é proporcional a B(t). Essas duas tensões são lidas
pelos canais 1 e 2 do osciloscópio. A operação no modo x-y (canal 1→ eixo x) exibe a
característica de histerese B(t)=f(H(t)) do núcleo magnético.
CEE – CONVERSÃO ELETROMECÂNICA DE ENERGIA
Perdas nos laços BH típicos
As perdas do ferro as podemos classificar em estáticas e dinâmicas, as estáticas são
constantes e não dependem da relação amper-espira (Ni) nem da freqüência ,no em tanto as
dinâmicas dependem da freqüência da corrente alternada e de seu modulo ( condições de carga
da maquina).
Ciclos de perdas do ferro
a) Somente perdas por histerese
b) Perdas por histerese e correntes de Foucault
c) Perdas por histerese, correntes Foucault e excedentes
Determinação das perdas por histerese
Suponhamos que um material ferromagnético seja submetido à ação de um campo magnético H
variável no tempo, com uma frequência f e período T = 1/f. Em cada período, uma parcela da
energia injetada no material será gasta apenas para percorrer o ciclo de histerese, e se constituirá
em perdas por histerese.
Denominando Ph a potência associada ao ciclo de histerese, e Wh a energia consumida em um
ciclo, temos:
A densidade volumétrica de energia magnética necessária para criar um indução magnética B é
dada por
𝐵
wh= ∫0 𝐻𝑑𝐵
e
Wt =whV
, onde V = volume do bloco
𝐵
A permissividade do material fica definida como a derivada na curva BH , μ = 𝐻𝑡
𝑡
CEE – CONVERSÃO ELETROMECÂNICA DE ENERGIA
BALANCE DE ENERGIA
CURVA DE HISTERESE
CEE – CONVERSÃO ELETROMECÂNICA DE ENERGIA
2. EXPERIMENTO
2.1 Material
Osciloscópio de dois canais, transformador com tap ajustável (Variac), transformador de teste,
capacitor de 1.5 F e resistores de 10 Ω e 100kΩ.
2.2 Montagem
a) Monte o circuito da Figura 2, com R1 = 10 Ω, R2= 100KΩ e C = 1.5 F. (1ptos)
b) Obtenha na tela do osciloscópio a curva da corrente de excitação em regime permanente e a
curva BH. (1ptos)
c) Obtenha o ciclo de histerese na tela do osciloscópio. Procure obter uma curva com amplitude
de Vr (t) suficientemente alta para que seja atingida a saturação magnética do material.
Determine os interceptos Hc e Bc (0.5pto)
d) Obtenha a densidade volumétrica da energia(wh) no ciclo [J/M3] e a energia total
𝐵
wh =∫0 𝐻𝑑𝑏 e
W=wh*V
(1pto)
e) A potencia perdida na histerese magnética por ciclo (1pto)
Ph=W*f
f) Faça um gráfico da permissividade absoluta no ciclo μ abs
g) Coenergia acumulada no bloco (1pto) (áreas iguais)
h) Fluxo de enlace maximo λmax (1pto)
i) Indutância por fluxo de enlace (1pto)
ϕmax= Bmax*A
L=
j) Indutância por energia armazenada (1pto)
𝑁1𝜙
𝑖
𝑖2
W = 𝐿2
𝐵
, μ = 𝐻𝑡
𝑡
(1pto)