Experimento 5 : Fenômenos de indução magnética – transformação

Experimento 5 : Fenômenos de indução magnética – transformação de
voltagem e ciclo de histerese
Grupo: Daniela Sato
Maria Silvia C. Franciscon
André De Caroli
RA: 090849
RA: 084489
RA: 072796

Resumo:
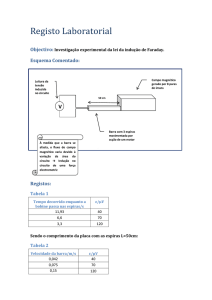
A partir do circuito mostrado na figura 4, procuramos estabelecer nesse
experimento a relação existente entre Vp e Vs, considerando situações
distintas como o núcleo de ferro com e sem a parte superior. A partir do
gráfico obtido, calculamos a razão entre o número de espiras do secundário
pelo do primário e comparamos com os reais valores utilizados.
Além disso, procuramos obter o ciclo de histerese com a montagem do
circuito da figura 5 e definir fisicamente o campo coercitivo HC e o cmapo
remanente BR.

Introdução:
O transformador é um dispositivo destinado a transmitir energia elétrica
ou potência elétrica de um circuito a outro, transformar tensões ou correntes,
além de outras funções. Esse dispositivo é constituído de duas ou mais
bobinas, ou enrolamentos, e um circuito magnético, que acopla tais bobinas.
Nesse experimento esperamos nos familiarizar com esse equipamento
através da montagem de circuitos e aplicação teórica.

Teoria:
Um transformador ideal tem acoplamento de 100%, é linear (não tem
saturação nem histerese) e não tem perdas ôhmicas. Como não há perdas de
acoplamento, temos que o fluxo magnético Φ no primário é passado
integralmente para o circuito secundário, e as voltagens no transformador são
dadas por:
𝑑Φ
𝑉𝑃 = −𝑁𝑃 𝑑𝑡
(1)
𝑉𝑆 = −𝑁𝑆
𝑑Φ
𝑑𝑡
(2)
onde NP e NS são os números de espiras das bobinas primária e secundária,
respectivamente.
Se igualarmos os termos 𝑑Φ/𝑑𝑡 das equações 1 e 2, teremos que:
𝑁
𝑉𝑆 = (𝑁 𝑆 ) 𝑉𝑃
𝑃
(3)
Para a próxima análise, devemos montar o circuito da figura 1, que está
mostrado a seguir.
Figura 1: Circuito montado para observar a curva de histerese de um
transformador.
No circuito da figura 1, as tensões Vx e Vy são, respectivamente, as tensões
medidas nos canais 1 e 2 do osciloscópio.
Agora, considere o transformador mostrado na figura 2.
Figura 2: Transformador, ilustrando o comprimento médio, l, e a seção reta
do núcleo, S.
Pela Lei de Ampère, sabemos que:
⃗ . 𝑑𝑙
𝐼𝑇 = ∮𝐻
𝑁𝑃 . 𝐼𝑃 = 𝐻𝑙
Sabendo que 𝐼𝑃 = 𝑉𝑃 ⁄𝑟 temos que:
𝑉𝑥
. 𝑁𝑃 = 𝐻𝑙
𝑟
𝑁
(4)
(5)
(6)
𝐻 = ( 𝑟𝑙𝑃 ) 𝑉𝑥
(7)
Também, considerando que o campo magnético é uniforme, e sabendo que o
⃗ . S⃗, este pode ser aproximado simplesmente
fluxo magnético é dado por Φ = B
por:
Φ = B. S (8)
Substituindo a equação 8 em 2, e sabendo que a área S é constante, temos
que:
𝑑𝐵
𝑉𝑆 = −𝑁𝑆 𝑆 𝑑𝑡 (9)
Do circuito da figura 1, sabemos que:
𝑡 𝑉𝑆 (𝑡)
𝑉𝑦 (𝑡) = ∫ 𝑅𝐶
𝑑𝑡
(10)
Substituindo a equação 9 em 10 e rearranjando para B, teremos que:
𝑅𝐶
𝐵(𝑡) = (𝑆𝑁 ) 𝑉𝑦 (𝑡)
(11)
𝑆
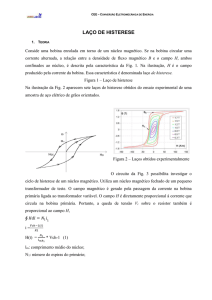
Se o osciloscópio for colocado no modo XY, poderemos observar a curva de
histerese, que será como a mostrada na figura 2.
Figura 3: Ciclo de histerese que pode ser observado no osciloscópio,
operando no modo XY.
Na figura 3, B é o campo magnético total dentro da barra (devido à corrente
da bobina e à imantação do ferro), H é o campo produzido pela corrente da
bobina, BR é o campo remanente e HC é o campo coercitivo.

Metodologia Experimental:
- Materiais:
Capacitor de 1 µF;
Resistências de 4,7 Ω e 100 kΩ;
Protoboard;
Osciloscópio;
Transformador variável;
Transformador de isolação (duas bobinas de 300 espiras montadas em
um núcleo de ferro);
Transformador Phywe com duas bobinas (400 e 1600 espiras).
- Métodos:
Primeiramente, deve-se montar o circuito da figura 4.
Figura 4: Circuito utilizado para a primeira parte do experimento.
No circuito da figura 4, a bobina no primário (esquerda no transformador
de teste) tem 400 espiras e a bobina no secundário (direita no transformador
de teste) tem 1600 espiras. Através desse circuito, obtivemos dados para VS
e VP, onde estes são os dados obtidos nos canais 1 e 2, respectivamente, e
pudemos montar um gráfico. Do gráfico, e da equação 3, sabemos que o
coeficiente angular será a relação 𝑁𝑠 ⁄𝑁𝑃 . Mas, como sabemos os valores de
NS e NP, podemos determinar o seu valor teórico.
Em seguida, removemos a parte superior do núcleo de ferro do
transformador de teste e mantivemos as espiras. Assim, obtivemos novos
valores para VS e VP, e pudemos fazer um novo gráfico, consequentemente
com uma nova razão 𝑁𝑠 ⁄𝑁𝑃 .
Por último, montamos o circuito da figura 5.
Figura 5: Circuito utilizado para investigar o ciclo de histerese.
No circuito da figura 5, r = 4,7 Ω, R = 100 kΩ, C = 1 μF e a bobina de
400 espiras está em série com r.
Colocando o osciloscópio no modo XY, veremos na tela o ciclo de
histerese.

Resultados e Análise de dados:
Com o circuito da figura 4, obtivemos os dados mostrados na tabela 1, a
seguir.
Tabela 1: Dados obtidos para as tensões no primário e no secundário.
VP (V)
0,4
0,5
0,5
0,7
0,8
0,9
1,1
1,2
1,4
1,4
1,5
2,0
∆VP (V)
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,2
VS (V)
1,1
1,4
1,7
2,1
2,5
2,9
3,5
3,7
4,0
4,3
4,7
5,1
∆VS (V)
0,1
0,1
0,1
0,2
0,2
0,2
0,2
0,2
0,2
0,2
0,2
0,3
Para calcularmos os erros das medidas, utilizamos a seguinte relação:
∆𝑉 = ±(3% 𝑑𝑜 𝑣𝑎𝑙𝑜𝑟 𝑑𝑒 𝑙𝑒𝑖𝑡𝑢𝑟𝑎 + 5% 𝑑𝑎 𝑒𝑠𝑐𝑎𝑙𝑎 𝑉/𝑑𝑖𝑣) (12)
A escala V/div utilizada neste experimento foi de 2 V/div.
Utilizando esses dados, pudemos construir o gráfico 1 apresentado a seguir.
Gráfico 1: Relação entre VS e VP para os dados coletados na tabela 1.
Como este gráfico foi plotado utilizando o programa Origin, nele pudemos
obter o valor do coeficiente angular da reta, que foi de 2,9 ±0,1. Se analisarmos
a equação 3, veremos que esse coeficiente corresponde a fração 𝑁𝑆 ⁄𝑁𝑃 . E, como
tínhamos o número de espiras de cada bobina, sabemos que seu valor teórico
deve ser de 𝑁𝑆 ⁄𝑁𝑃 = 1600⁄400 = 4.
Como podemos perceber, o erro relativo entre a medida teórica e a prática
foi de 25%. Podemos apontar como causa deste erro o fato de que o indutor não
é ideal, portanto há perdas ôhmicas e há histerese.
Em seguida, retirando a parte superior do núcleo de ferro do transformador
de teste, obtivemos novos valores de VS e VP, os quais são mostrados na tabela
2.
Tabela 2: Valores para VS e VP para o núcleo aberto.
VP (V)
0,3
0,8
1,0
1,2
1,3
1,4
1,5
1,7
2,0
2,0
∆VP (V)
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,2
0,2
0,2
VS (V)
0,5
1,1
1,5
1,7
2,0
2,3
2,6
3,2
3,8
4,5
∆VS (V)
0,1
0,1
0,1
0,1
0,2
0,2
0,2
0,2
0,2
0,2
Os erros da tabela 2 foram calculados pela equação 12, como o feito
anteriormente para a tabela 1.
A partir dos dados da tabela 2, pudemos constriur o gráfico 2 mostrado a
seguir.
Gráfico 2: Relação entre VS e VP para os dados coletados na tabela 2.
A partir desse gráfico, obtemos que o valor do coeficiente angular da reta é
de 2,02 ±0,09. E seu valor teórico é o mesmo utilizado anteriormente, pois foi
mantido o número de espiras das bobinas.
Esse novo valor para a razão NS/NP tem um erro de cerca de 50% do valor
teórico. Como foi retirada a parte superior do núcleo de ferro, as perdas ôhmicas
são ainda maiores.
Se compararmos os gráficos 1 e 2, veremos que as inclinações das retas são
bem diferentes, sendo que no gráfico 2 esta possui um coeficiente linear menor.
Isso se deve ao fato de que o valor de l será menor, e da equação 7 podemos
observar que, se esse valor diminui, o valor de Vx também diminui. Logo, isso
irá diminuir a inclinação da reta.
Por último, montamos o circuito da figura 5, como descrito anteriormente.
Alterando o osciloscópio para o modo XY, obtivemos o ciclo de histerese
mostrado na figura 6.
Figura 6: Ciclo de histerese obtido na frequência de 60 Hz.
No ciclo de histerese da figura 6, o ponto onde este corta o eixo vertical é
chamado de campo remanente (BR). O campo remanente é o valor do campo
magnético total dentro da barra onde não há passagem de corrente elétrica (IP =
0), ficando como um imã. Para zerar esse campo magnético, é necessário aplicar
um campo magnético no sentido oposto, este é chamado de campo coercitivo
(HC).

Discussão e Conclusão:
A partir dos dados experimentais obtidos, e comparando-os com o valor
teórico, podemos observar que houve uma diferença relativamente alta entre
eles. Boa parte dessa diferença pode ter sido causada por perdas ôhmicas e
pelo fato do transformador não ser linear, ou seja, há saturação e histerese.
Outras possibilidades de erro consistem em erro do experimentador e
aqueles devido a imprecisão de valores oscilatórios mostrados no
osciloscópio.

Referências Bibliográficas:
Fragnito H., Apostila de Fisica Experimental IV, (Unicamp,SP, 2009), pp
51-59. Disponível em http://www.ifi.unicamp.br/~calderon/livro.pdf.
Acesso em 22/09/2010.