Força no entreferro - udesc

UNIVERSIDADE DO ESTADO DE SANTA CATARINA
CENTRO DE CIÊNCIAS TECNOLÓGICAS – CCT
DEPARTAMENTO DE ENGENHARIA ELÉTRICA - DEE
LABORATÓRIO DE CONVERSÃO ELETROMECÂNICA DE
ENERGIA
Experimento 6 –Laço de histerese
1. OBJETIVO
Obter a curva BH do material magnético de um transformador monofásico por meio do ensaio
experimental. A partir da curva BH, identificar o tipo do material (mole, intermediário, duro), perdas no ferro e
permeabilidade.
2. PARTE TEÓRICA
a. Laço de histerese
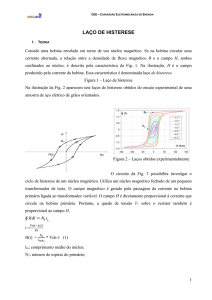
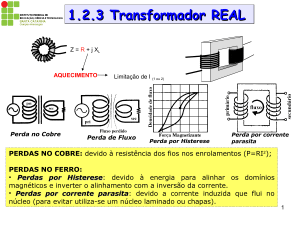
Considere uma bobina enrolada em torno de um núcleo magnético. Se na bobina circular uma corrente
alternada, a relação entre a densidade de fluxo magnético B e o campo H, ambos confinados ao núcleo, é
descrita pela característica da Fig. 1. Na ilustração, H é o campo produzido pela corrente da bobina. Essa
característica é denominada laço de histerese.
Figura 1 – Laço de histerese
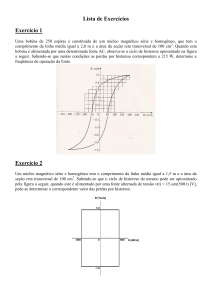
Na ilustração da Fig. 2 aparecem sete laços de histerese obtidos do ensaio experimental de uma amostra
de aço elétrico de grãos orientados.
Figura 2 – Laços obtidos experimentalmente
O circuito da Fig. 3 possibilita investigar o ciclo de histerese de um núcleo magnético utiliza um núcleo
magnético fechado de um pequeno transformador de teste.
1/9
UNIVERSIDADE DO ESTADO DE SANTA CATARINA
CENTRO DE CIÊNCIAS TECNOLÓGICAS – CCT
DEPARTAMENTO DE ENGENHARIA ELÉTRICA - DEE
LABORATÓRIO DE CONVERSÃO ELETROMECÂNICA DE
ENERGIA
Figura 3 – Circuito para investigar o laço de histerese.
O campo magnético é gerado pela passagem da corrente na bobina primária ligada ao transformador
variável. O campo H é diretamente proporcional à corrente que circula na bobina primária e pode ser obtido a
partir da lei de Ampere.
∮
𝐻𝑑𝑙 = 𝑁1 𝑖1
𝐿(𝑆)
A corrente pode ser obtida indiretamente pela leitura da queda de tensão no resistor 𝑅1 .
𝑖1 =
𝑉𝑐ℎ1 (𝑡)
𝑅1
Por fim, a queda de tensão 𝑉𝑟 sobre o resistor também é proporcional ao campo H.
𝐻(𝑡) =
𝑁1
𝑙𝑚𝑒𝑑
𝑉𝑐ℎ1
𝑙𝑚 - comprimento médio do núcleo;
𝑁1 - número de espiras do primário;
De acordo com a lei de Faraday, a tensão 𝑉2 na bobina secundária é diretamente proporcional à derivada
do fluxo total em relação ao tempo.
𝑑𝜙(𝑡)
𝑉2 = 𝑁2
𝑑𝑡
O circuito RC conectado no secundário é utilizado para integrar o sinal da tensão 𝑉2. Admitindo-se que a
queda de tensão ocorre no resistor 𝑅2 = 100𝑘Ω, pode-se escrever a relação da tensão com a corrente no
secundário:
2/9
UNIVERSIDADE DO ESTADO DE SANTA CATARINA
CENTRO DE CIÊNCIAS TECNOLÓGICAS – CCT
DEPARTAMENTO DE ENGENHARIA ELÉTRICA - DEE
LABORATÓRIO DE CONVERSÃO ELETROMECÂNICA DE
ENERGIA
𝑉2 = 𝑖𝑐 𝑅2
Lembrando que a corrente no capacitor é dada por:
𝑖𝑐 = 𝐶
𝑑𝑉𝑐 (𝑡)
𝑑𝑡
Juntando as expressões, tem-se:
𝑅2 𝐶
𝑑𝑉𝑐 (𝑡)
𝑑𝜙(𝑡)
= 𝑁2
𝑑𝑡
𝑑𝑡
Isolando a derivada do fluxo, tem-se:
𝑑𝜙(𝑡) 𝑅2 𝐶 𝑑𝑉𝑐 (𝑡)
=
𝑑𝑡
𝑁2 𝑑𝑡
Integrando ambos os lados em relação ao tempo, tem-se:
𝜙(𝑡) =
𝑅2 𝐶
𝑉 (𝑡)
𝑁2 𝑐
Supondo que o fluxo é constante na seção magnética 𝐴𝑚 , tem-se que o fluxo é dado por:
Φ = 𝐵(𝑡)𝐴𝑚
No circuito a tensão 𝑉𝑐 (𝑡) será a tensão medida no canal 2, ou seja, 𝑉𝑐ℎ2 (𝑡), logo a densidade de fluxo
magnético 𝐵(𝑡), é dada por:
𝐵(𝑡) =
𝑅2 𝐶
𝑉 (𝑡)
𝑁2 𝐴𝑚 𝑐ℎ2
𝐴𝑚 : área transversal do núcleo;
𝑁2 : número de espiras do secundário;
3/9
UNIVERSIDADE DO ESTADO DE SANTA CATARINA
CENTRO DE CIÊNCIAS TECNOLÓGICAS – CCT
DEPARTAMENTO DE ENGENHARIA ELÉTRICA - DEE
LABORATÓRIO DE CONVERSÃO ELETROMECÂNICA DE
ENERGIA
Em resumo a tensão 𝑉𝑟1 (𝑡) é proporcional a 𝐻(𝑡) e 𝑉𝑐 (𝑡) é proporcional a 𝐵(𝑡). Essas duas tensões são
lidas pelos canais 1 e 2 do osciloscópio. A operação no modo x-y (canal 1→ eixo x) exibe a característica de
histerese B(t)=f(H(t)) do núcleo magnético.
Pontos notórios da curva
Fig. ( ) O efeito de histerese é gerado pela resistência à movimentação de paredes de domínio.
Materiais ferromagnéticos que possuem uma coercividade alta são denominados Duros (coercividade
maior que 104 A/m); aqueles que possuem coercividade baixa são denominados Moles ou Doces (coercividade
menor que 500 A/m).
O material Duro geralmente tem aplicações na fabricação de imã, os Moles em projetos de eletrônica de
potência, por sua estreita curva existe pouca dissipação de potência.
4/9
UNIVERSIDADE DO ESTADO DE SANTA CATARINA
CENTRO DE CIÊNCIAS TECNOLÓGICAS – CCT
DEPARTAMENTO DE ENGENHARIA ELÉTRICA - DEE
LABORATÓRIO DE CONVERSÃO ELETROMECÂNICA DE
ENERGIA
Curva de magnetização BH
2
1.5
Indução [T]
1
Inferior
Sup
0.5
BH
0
-100
0
100
200
300
400
500
600
700
800
900
1000
-0.5
-1
Intensidade de campo H[A/m]
b. Perdas no ferro
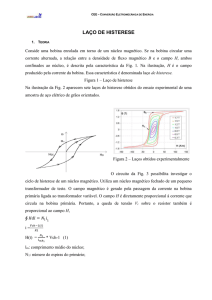
As perdas no ferro podem ser estimadas a partir do laço de histerese. Para cada laço de histerese, tem-se
diferentes informações sobre as perdas no ferro, conforme figura abaixo:
Ciclos de perdas do ferro
a) Somente perdas por histerese (frequência muito baixa 1 a 3Hz)
b) Perdas por histerese e correntes de Foucault
c) Perdas por histerese, correntes Foucault e excedentes
5/9
UNIVERSIDADE DO ESTADO DE SANTA CATARINA
CENTRO DE CIÊNCIAS TECNOLÓGICAS – CCT
DEPARTAMENTO DE ENGENHARIA ELÉTRICA - DEE
LABORATÓRIO DE CONVERSÃO ELETROMECÂNICA DE
ENERGIA
As perdas magnéticas totais que ocorrem num material ferromagnético quando sujeito à ação de um
campo de indução B variável no tempo são dadas por:
𝑃𝑓𝑒𝑟𝑟𝑜 = 𝑃ℎ𝑖𝑠𝑡𝑒𝑟𝑒𝑠𝑒 + 𝑃𝑓𝑜𝑢𝑐𝑎𝑢𝑙𝑡 + 𝑃𝑒𝑥𝑐𝑒𝑑𝑒𝑛𝑡𝑒𝑠
Onde :
Ph: Representa as perdas por histerese
Pf: São as chamadas perdas por correntes de Foucault clássicas
Pexc: São as perdas por correntes de Foucault excedentes ou, anômalas.
Por vezes pode também ser adotada a divisão em perdas estáticas e dinâmicas em que, as primeiras
correspondem às perdas por histerese, e as segundas às perdas por correntes de Foucault clássicas e excedentes.
As perdas por histerese, 𝑃ℎ , numa amostra de material ferromagnético são proporcionais à área do ciclo de
histerese, obtido em regime quase-estático, multiplicada pelo volume da amostra, Vol e pela frequência de
operação f, isto é,
𝑃ℎ = ∮ 𝐻𝑑𝐵 × 𝑓 × 𝑉𝑜𝑙
c. Relações para o cálculo das indutâncias
Da lei de Faraday
V1  n1
V1 
d di1
di1 dt
=> pode ser rescrita como:
di
n1 An1
 (i ) i1
lm
dt
De forma análoga para o circuito secundário:
V2  n2
d di1
di1 dt
A tensão induzida no secundário pode ser escrita como:
V2  n2
An1
di
(i ) 1
lm
dt
A tensão induzida no bobinado secundário produto da variação na corrente do primário
6/9
UNIVERSIDADE DO ESTADO DE SANTA CATARINA
CENTRO DE CIÊNCIAS TECNOLÓGICAS – CCT
DEPARTAMENTO DE ENGENHARIA ELÉTRICA - DEE
LABORATÓRIO DE CONVERSÃO ELETROMECÂNICA DE
ENERGIA
 A
 di
V12  n2 n1  (i1)  1
 lm
 dt
[V]
A tensão induzida no bobinado secundário e proporcional a variação da corrente primária
V12  M 12
di1
dt
[V]
O fator que multiplica a derivada da corrente depende de questões construtivas é a variação da permeabilidade em
função da corrente é definido como indutância mútua.
M 12  n1 n2
A
 (i1) [H]
lm
De forma análoga a tensão induzida no primário por efeito da corrente secundária.
 A
 di
V21  n1 n2  (i 2)  2 [V]
 lm
 dt
A indutância que aparece no bobinado primário produto da variação da corrente secundária
M 21  n1 n2
A
 (i 2)
lm
[H]
Assim
M21= M12= M =
n1n2
A
 ( i ) , da mesma forma para as indutâncias próprias:
lm
An12
L1 
 (i )
lm
An22
L2 
 (i )
lm
7/9
UNIVERSIDADE DO ESTADO DE SANTA CATARINA
CENTRO DE CIÊNCIAS TECNOLÓGICAS – CCT
DEPARTAMENTO DE ENGENHARIA ELÉTRICA - DEE
LABORATÓRIO DE CONVERSÃO ELETROMECÂNICA DE
ENERGIA
Como nos três casos a derivada é a mesma. O comprimento médio, e a área são os mesmos, podemos relacionar as
indutâncias pela expressão:
L1 L 2
M
 2 
2
n1
n2 n1n2
A relação de transformação é definida como a 
n1
, utilizando a relação de transformação, a indutância mútua pode
n2
ser expressa em função da indutância própria primária ou secundária.
L1
M

/ n12
2
n1 n1n2
=> L1= Ma => M=
L1
a
De forma análoga:
L2
M

/ n22
2
n2 n1n2
=> M=a*L2
Isto é, a indutância mútua pode ser calculada em função da indutância primária ou secundária desde que a relação
de transformação seja conhecida.
3. Ensaio
Material
Osciloscópio de dois canais
transformador com tap ajustável (Variac)
transformador de teste
capacitor de 1.5 F
resistores de 1 Ω e 300kΩ.
Montagem
a) Monte o circuito da Figura 2, com R1 = 1 Ω, R2= 300kΩ e C = 1.5 F.
b) Obtenha curva da corrente de excitação em regime permanente e a curva BH.
c) Obtenha o ciclo de histerese na tela do osciloscópio. Procure obter uma curva com amplitude de Vr (t)
suficientemente alta para que seja atingida a saturação magnética do material.
8/9
UNIVERSIDADE DO ESTADO DE SANTA CATARINA
CENTRO DE CIÊNCIAS TECNOLÓGICAS – CCT
DEPARTAMENTO DE ENGENHARIA ELÉTRICA - DEE
LABORATÓRIO DE CONVERSÃO ELETROMECÂNICA DE
ENERGIA
4. Questões
a) Determine os interceptos Hc e Bc.
b) Determine se o material é duro ou doce
c) Obtenha curva BH
d) Obter a permeabilidade máxima do material.
e) Obtenha a densidade volumétrica da energia(wh) no ciclo [J/M3] e a energia total

𝐵
wh =∫0 𝐻𝑑𝑏
e
W=wh*V
f) A potencia perdida no ferro por ciclo Pfe=W*f
g) Coenergia acumulada no bloco
h) Fluxo de enlace maximo λmax
i)
Indutância própria primária L1
j)
Indutancia secundaria L2
ϕmax= Bmax*A
k) Indutancia mútua
5.
a)
b)
c)
d)
AVALIAÇÃO
(1,0) Presença
(4,0) Experimento
(4,0) Questões
(1,0) Relatório
9/9