resistência dos materiais i

UNIVERSIDADE FEDERAL DE GOIÁS
ESCOLA DE ENGENHARIA CIVIL
RESISTÊNCIA DOS MATERIAIS I
Duração: 3 hr 00 min.
Data: 23/06/2012
TERCEIRA PROVA
NOME: _____________________________________________ Matrícula: _____________
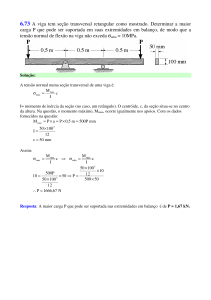
1. O elemento infinitesimal de um ponto pode
ser visto na Fig. 01. Suponha que o elemento está
em dois estados diferentes: a) Estado Plano de
Tensões (EPT) no plano xy e, b) Estado Plano de
Deformações (EPD) no plano xy. Pede-se a)
Calcular a variação de volume do elemento
infinitesinal para cada um dos estados; b)
Demonstrar quando a variação de volume dos dois
estados será a mesma. (2,5 pts)
Calcular o deslocamento no início da viga. Os
cabos têm diâmetro d = 1 cm e todo o sistema é
feito de aço com E = 200 GPa. (2,5 pts)
50 kN/m
y
dz
yz
zy
yx 
xy
A
x
5 cm
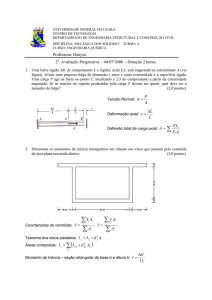
Figura 03
Figura 01
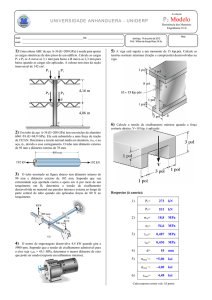
2. Uma viga em balanço tem seção retangular de
base b, altura variável h(x) e suporta uma carga
triangular com visto na Fig. 02. Pede-se: a)
Calcular a expressão da altura h(x) de forma que
em toda a viga, as tensões normais máximas
sejam sempre adm; b) Fazer um esboço da
variação da altura da viga h(x) ao longo do
comprimento; c) Calcule a equação da linha
elástica da viga (use o método da integração); d)
Calcular o deslocamento máximo da viga.
Considere b = 2 cm, E = 13 GPa e adm = 50 MPa.
(2,0 pts)
b
20 kN/m
1 cm
5 cm
dx
z
B
1 cm
zx xz
dy
3m
30 kN/m
2m
h(x)
4. Das informações de um estudo experimental,
são conhecidas as tensões em duas direções
diferentes sendo: (x, xy) = (75.3 MPa, -18.6
MPa) e (x, xy) = (0.0 MPa, 33.0 MPa). Usando o
círculo de Mohr calcule: a) As tensões principais e
as tensões cisalhantes máximas (desenhe cada um
dos estados; b) Calcule as tensões para um plano
orientado um ângulo  = 60º, no sentido antihorário a partir da tensão principal 1. (1,5 pts)
5. Uma régua de aço fina de alta resistência com
espessura t = 0,10 in. e comprimento L = 30 in. é
flexionada por um momento Mo, dando a forma de
um arco circular com ângulo central  = 60º ou
/3 rad como mostrado na Fig. 04. Qual é a tensão
normal máxima max na régua? E = 29 ksi.
(1,5 pts)
t
3m
Figura 02
3. Uma viga de seção transversal T invertida,
está suspensa por dois cabos e suporta as cargas
mostradas na Fig. 03. Pede-se: a) Desenhar os
diagramas de esforço cortante e momento fletor;
b) Calcular a equação da linha elástica da viga; c)
Mo
Mo

Figura 04
EQUAÇÕES NECESSÁRIAS NA SOLUÇÃO
wo
 Equilíbrio:
 Fx  0  Fy  0  M  0
x
 Deformação axial
a
PL

EA
 Lei de Hooke generalizada
1
 x   x   y   z
E
1
 y   y    x   z 
E
1
 z   z   x   y
E
1
 xy   xy
G
 Modulo do cisalhamento
E
G
21   


M
 Tensão normal:    y
I






 Deformação:   


y
 ~y A
y
A
~

 Momento de inércia: I    I  A d 2 


 Deflexão de vigas:
d 4v
d 3v
EI
  w( x), EI
 V ( x)
4
dx
d x3
M 
x
a
w  m  x  a 1
M 
m
 x  a 3
6
 Integrais das funções singulares:
 x  a  n 1
 C para n  0
n 1
n
n 1
para n  1,  2
  x  a  dx  x  a 
 x a 
n
dx 
 Transformação de tensões:
 x´ 

 Posição da linha neutra:
wo
 x  a 2
2
Inclinação = m
w  wo  x  a 0
 x  y
2
 x´ y´  
 y´ 
 x  y
2
 x  y
 x  y
2

2

d v
dv
 M ( x), EI
  ( x)
dx
d x2
x
 1, 2 
 x  y
cos 2   xy sen2
2
tg 2 p 
 max
  
x
y
 
2


 xy
 
x
y
 
2



x
2

  2
xy


 y  2
x
 xy
M  M o  x  a 0
P
 Centro do círculo de Mohr:
 med 
 x  y
2
 Raio do círculo de Mohr:
a
w  P  x  a 1 M  P  x  a 1
2

  2
xy


    2
 x
y


tg 2  c  
a
w  M o  x  a 2
2
 Tensões principais
 Funções singulares (carga e momento):
Mo
sen 2   xy cos 2
 x  y
2
EI
cos 2   xy sen 2
  
x
y
R  
2


2

  2
xy

