AP2_2006 - DEECC - Universidade Federal do Ceará

UNIVERSIDADE FEDERAL DO CEARÁ
CENTRO DE TECNOLOGIA
DEPARTAMENTO DE ENGENHARIA ESTRUTURAL E CONSTRUÇÃO CIVIL
DISCIPLINA: MECÂNICA DOS SÓLIDOS I – TURMA A
CURSO: ENGENHARIA QUÍMICA
Professora: Denyse.
2a. Avaliação Progressiva – 04/07/2006 – Duração 2 horas.
1. Uma barra rígida AB, de comprimento L e rigidez axial EA, está engastada na extremidade A (ver
figura). Existe uma pequena folga de dimensão s entre a outra extremidade e a superfície rígida.
Uma carga P age na barra no ponto C, localizado a 2/3 do comprimento a partir da extremidade
engastada. Se as reações no suporte produzidas pela carga P devem ser iguais, qual deve ser o
tamanho da folga?
(2,0 pontos)
Tensão Normal: σ =
P
A
Deformação axial: ε =
∆L
L
Deflexão total de carga axial: δ =
Pi Li
∑EA
i
i
i
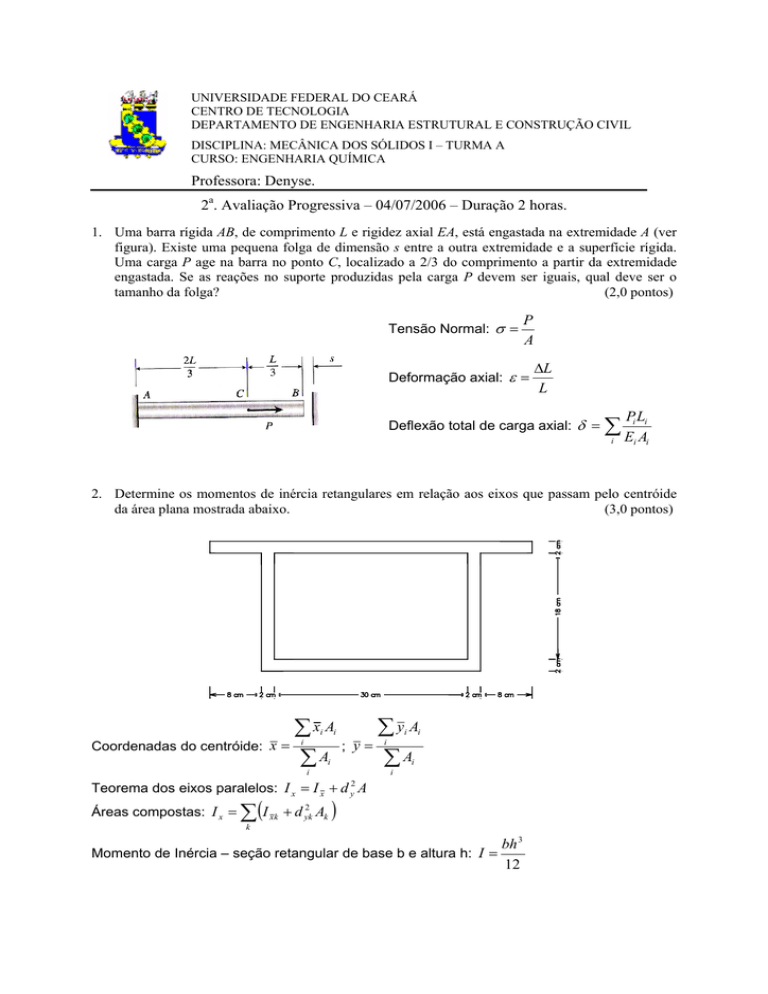
2. Determine os momentos de inércia retangulares em relação aos eixos que passam pelo centróide
da área plana mostrada abaixo.
(3,0 pontos)
∑x A
x=
;
∑A
i
Coordenadas do centróide:
i
i
i
i
∑y A
y=
∑A
i
i
i
i
i
Teorema dos eixos paralelos: I x = I x + d y2 A
Áreas compostas: I x =
∑ (I
xk
+ d yk2 Ak
)
k
Momento de Inércia – seção retangular de base b e altura h: I =
bh 3
12
3. Uma viga de madeira ABC simplesmente apoiada em A e em B e com um segmento suspenso em
BC tem altura h = 280 mm (ver figura). O comprimento do vão principal da viga é L = 3,6 m e o
comprimento do segmento estendido é L/3 = 1,2 m. A viga suporta uma carga concentrada 3P =
15 kN no ponto médio do vão principal e uma carga P = 5kN na extremidade livre do segmento
suspenso. Determine a largura b da viga exigida com base na tensão de flexão admissível de 8,2
MPa.
(2,5 pontos)
Equações de equilíbrio 2D:
∑F = 0
∑F = 0
∑M = 0
x
y
O
Tensão Normal: σ = −
My
I
4. Uma viga curva ABC de eixo circular (raio r = 300 mm) é carregada pelas forças P = 1,6 N (ver
figura). A seção transversal da viga é retangular com altura h e espessura t. Se a tensão de tração
permitida é 80 MPa e a altura h = 30 mm, qual é a mínima espessura exigida tmin?
(2,5 pontos)
Tensão de flexão em vigas de eixo curvo:
σ =
M (r − R)
; e=r −R
Aer
Expressão para R – seção retangular de
altura h:
R=
h
r
ln 2
r1
5. (Opcional para quem entregar toda a lista resolvida. Substitui a terceira ou a quarta questão)
Determinar, para a barra e o carregamento indicados, o erro relativo que se comete no cálculo da
tensão máxima, considerando-se que a barra tem eixo reto. Considerar r = 300 mm. (2,5 pontos)
Tensão de flexão em vigas de eixo curvo:
σ =
M (r − R)
; e=r −R
Aer
Expressão para R – seção retangular de
altura h:
R=
h
r
ln 2
r1
Tensão de flexão em vigas de eixo reto:
σ =−
My
I