resistência dos materiais i

UNIVERSIDADE FEDERAL DE GOIÁS
ESCOLA DE ENGENHARIA CIVIL
RESISTÊNCIA DOS MATERIAIS I
Duração: 3 hr 00 min.
Data: 10/12/2011
TERCEIRA PROVA
NOME: __________________________________________________ Matrícula: _____________
1.
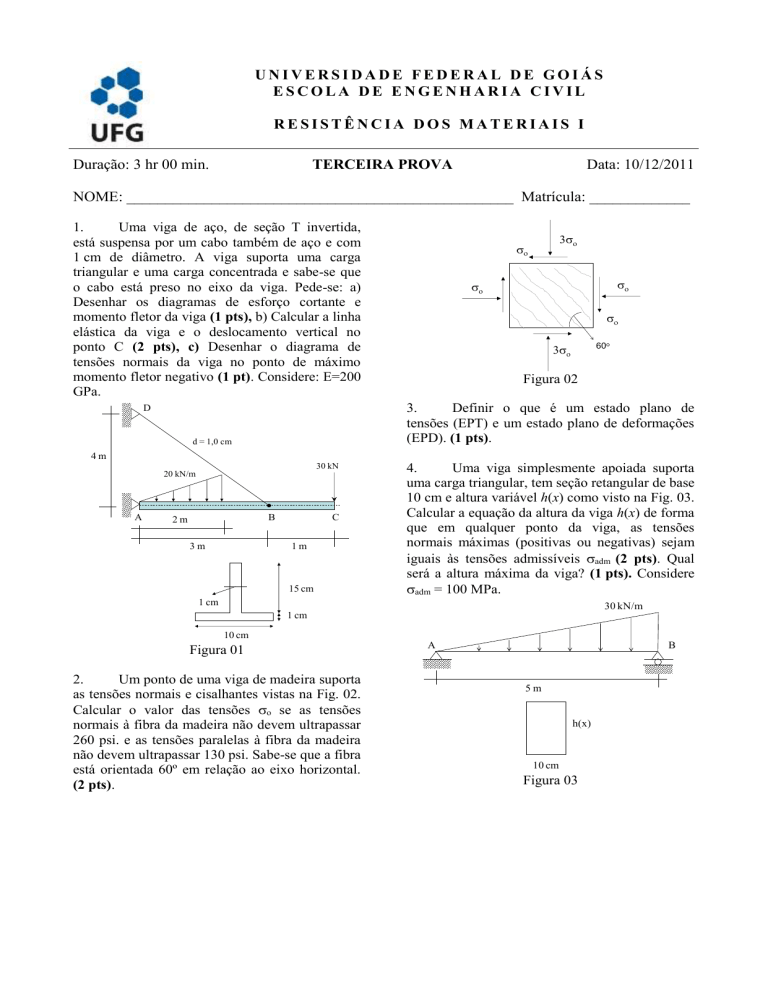
Uma viga de aço, de seção T invertida,
está suspensa por um cabo também de aço e com
1 cm de diâmetro. A viga suporta uma carga
triangular e uma carga concentrada e sabe-se que
o cabo está preso no eixo da viga. Pede-se: a)
Desenhar os diagramas de esforço cortante e
momento fletor da viga (1 pts), b) Calcular a linha
elástica da viga e o deslocamento vertical no
ponto C (2 pts), c) Desenhar o diagrama de
tensões normais da viga no ponto de máximo
momento fletor negativo (1 pt). Considere: E=200
GPa.
3o
o
o
o
o
60o
3o
Figura 02
3.
Definir o que é um estado plano de
tensões (EPT) e um estado plano de deformações
(EPD). (1 pts).
D
d = 1,0 cm
4m
30 kN
20 kN/m
A
B
2m
3m
C
1m
15 cm
4.
Uma viga simplesmente apoiada suporta
uma carga triangular, tem seção retangular de base
10 cm e altura variável h(x) como visto na Fig. 03.
Calcular a equação da altura da viga h(x) de forma
que em qualquer ponto da viga, as tensões
normais máximas (positivas ou negativas) sejam
iguais às tensões admissíveis adm (2 pts). Qual
será a altura máxima da viga? (1 pts). Considere
adm = 100 MPa.
1 cm
30 kN/m
1 cm
10 cm
Figura 01
2.
Um ponto de uma viga de madeira suporta
as tensões normais e cisalhantes vistas na Fig. 02.
Calcular o valor das tensões o se as tensões
normais à fibra da madeira não devem ultrapassar
260 psi. e as tensões paralelas à fibra da madeira
não devem ultrapassar 130 psi. Sabe-se que a fibra
está orientada 60º em relação ao eixo horizontal.
(2 pts).
A
B
5m
h(x)
10 cm
Figura 03
EQUAÇÕES NECESSÁRIAS NA SOLUÇÃO
 Equilíbrio:
 Fx  0
 Fy  0
M  0
 Deformação axial
 x a 
n
 x  a  n 1
C
n 1
dx  x  a  n 1
para n  0
para n  1,  2
 Transformação de tensões:

 Tensão normal:   
PL
EA
 x´ 
 x  y
2
 x´ y´  
M
y
I
 Posição da linha neutra:
 ~y A
y
A
~

 y´ 


 Momento de inércia: I    I  A d 2 
 Deflexão de vigas:
2
d 2v
dv
EI
 M ( x), EI
  ( x)
dx
d x2
 Funções singulares (carga e momento):
Mo
2
2

sen 2   xy cos 2
 x  y
2
 x  y
cos 2   xy sen 2
2
  
x
y
 
2


tg 2 p 
 max
 xy
 
x
y
 
2



2

  2
xy


 y  2
x
 xy
a
w  M o  x  a 2
M  M o  x  a 0
 Centro do círculo de Mohr:
 med 
P
 x  y
  
x
y
R  
2


a
w  P  x  a 1 M  P  x  a 1
wo
x
a
wo
 x  a 2
2
Inclinação = m
w  wo  x  a 0
M 
x
a
w  m  x  a 1
M 
2
 Raio do círculo de Mohr:
x
m
 x  a 3
6
 Integrais das funções singulares:
2

  2
xy


    2
 x
y


tg 2  c  
x
cos 2   xy sen2
 Tensões principais
3
d v
d v
  w( x), EI
 V ( x)
d x4
d x3
 x  y

 x  y
 x  y
 1,2 
4
EI
n
  x  a  dx 
2

  2
xy

