2a. Lista de Exercícios - DEECC

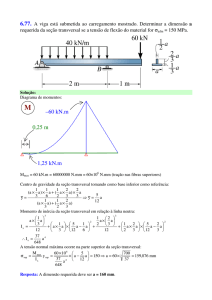
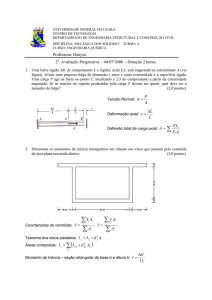
UNIVERSIDADE FEDERAL DO CEARÁ
CENTRO DE TECNOLOGIA
DEPARTAMENTO DE ENGENHARIA ESTRUTURAL E CONSTRUÇÃO CIVIL
2a. LISTA DE EXERCÍCOS – 2006.1
Profa. Tereza Denyse P. de Araújo
1.
Uma barra de aço de seção circular de diâmetro D = 3 cm engastada em uma extremidade
e livre na outra, está submetida a uma ação de três forças, como representa a Figura 1. Os
valores das forças são: P1 = 100 kN; P2 = 140 kN e P3 = 120 kN. Pede-se: (a) Calcular as
forças normais nos trechos 1-2, 2-3, 3-4; (b) Calcular as tensões normais nos trechos 1-2,
2-3, 3-4; (c) Calcular os deslocamentos elásticos das seções I-I, II-II e III-III.
Figura 1
Figura 2
2.
O sistema mostrado na Figura 2, formado pelas barras 1 e 2 de materiais diferentes, foi
projetado para que uma carga P = 75 kN aplicada em A fechasse o contato entre os fios B
e C e disparasse um alarme indicando o nível de carga. (a) Verifique qual deve ser o valor
de δ1 para que o sistema dispare, sendo o módulo de elasticidade E1 = 69,0 GPa e E2 =
105 GPa. As áreas A1 = 3,0 cm2 e A2 = 2,6 cm2. O comprimentos são L1 = 20,0 cm e L2 =
40,0 cm. (b) Se o material 1 tem uma tensão de escoamento σ1Y = 255,0 MPa (tensão de
escoamento à tração) e para o material 2 σ2Y = 435,0 MPa, considerando ainda um
coeficiente de segurança igual a 1,5, verifique se a estrutura suporta esta carga com
segurança.
3.
Uma carga de compressão P é transmitida através de uma placa rígida para três barras de
liga de magnésio que são idênticas exceto que inicialmente a barra do meio é
ligeiramente mais curta do que as outras barras (veja a Figura 3). As dimensões e
propriedades do conjunto são as seguintes: comprimento L = 1,0 m, área de seção
transversal de cada barra A = 3000 mm2, módulo de elasticidade transversal E = 45 GPa e
folga s = 1,0 mm. (a) Calcule a carga P1 exigida para fechar a folga. (b) Calcule o
deslocamento para baixo δ da placa rígida quando P = 400 kN.
Figura 4
Figura 3
4.
Uma barra tracionada é composta de dois pedaços de material que são colados ao longo
da linha mn (Figura 4). Por razões práticas, o ângulo θ é limitado à faixa de 0º a 60º. A
tensão de cisalhamento admissível, τadm, na junta colada é ¾ da tensão de tração
admissível (σadm). Qual deve ser o valor do ângulo θ, afim de que a barra suporte o
máximo de carga P, admitindo que a resistência da junta colada controle o projeto.
5.
Um abajur de 25 N foi pendurado no teto por meio dos fios de alimentação da corrente
elétrica de comprimento igual a 0,75 m. Estes fios são de cobre e têm área total de seção
transversal igual a 3,2 mm2. A. O cobre tem as seguintes propriedades: módulo de
elasticidade E = 112 GPa, tensão de escoamento σY = 60 MPa e peso específico γ = 8, 63
× 104 N/m3. (a) Adotando um coeficiente de segurança C.S. = 1,5 em relação à tensão de
escoamento (σY) e desprezando o peso próprio dos fios, verifique a segurança quanto ao
comportamento estrutural. (b) Quanto o abajur descerá após a instalação? Considere o
abajur como um corpo rígido.
6.
Para as figuras planas abaixo, determine as coordenadas do centróide e os momentos de
inércia em relação aos eixos baricêntricos.
(b)
(a)
(c)
(d)
Figura 5
7.
Uma viga de aço ABC é simplesmente apoiada em A e B e tem um segmento suspenso BC
de comprimento L = 150 mm (veja Figura 6). A viga suporta um carregamento uniforme
de intensidade q = 3,5 kN/m ao longo de todo o seu comprimento de 450 mm. A seção
transversal da viga é retangular com largura b e altura 2b. A tensão normal de flexão
admissível no aço é σadm = 60 MPa. (a) Esboce os diagramas de momento fletor e esforço
cortante para a viga. (b) Desconsiderando o peso da viga, calcule a largura exigida b da
seção transversal retangular.
Figura 6
8.
Uma viga colada e laminada é feita colando-se n placas de largura b e espessura t, como
ilustrado na Figura 7 abaixo. Deduza uma expressão que relacione o valor do módulo da
I
seção W ( W =
) com o número de placas usadas para fazer a viga. Considere que a
y max
espessura de cada camada de cola é desprezível e que a viga laminada atua como uma
viga comum de madeira.
Figura 7
9.
Para a barra e o carregamento indicados na Figura 8, determinar o erro relativo que se
comete no cálculo da tensão máxima, considerando-se que a barra tem eixo reto.
Considerar r = 300 mm.
Figura 8
Figura 9
10. A barra de eixo curvo, indicada na Figura 9, tem seção transversal circular com 25,5 mm
de diâmetro. Determinar o maior valor do conjugado M, que atua em torno de um eixo
longitudinal, que a barra pode suportar, se a tensão máxima não pode exceder a 62 MPa.